Derivative by increment method (By definition with limit)
Summary
TLDRIn this video, the concept of calculating the derivative of the function f(x) = 2x + 1 is explained using the increment method, also known as the definition of a derivative via limits. The process involves calculating f(x + delta x), simplifying the expression, and finding the difference between f(x + delta x) and f(x). After simplifying the fraction, the limit as delta x approaches zero is taken, leading to the derivative. The video concludes with a similar exercise for viewers to practice and encourages engagement through likes, subscriptions, and comments.
Takeaways
- 😀 The derivative of a function can be calculated using the method of increments, which involves applying the limit definition of the derivative.
- 😀 The formula for the derivative is: f'(x) = lim(Δx → 0) [(f(x + Δx) - f(x)) / Δx].
- 😀 To begin, substitute x with (x + Δx) in the original function to calculate f(x + Δx).
- 😀 After substitution, simplify the expression for f(x + Δx) by distributing and combining like terms.
- 😀 Once f(x + Δx) is calculated, subtract f(x) from it to find the numerator in the derivative formula.
- 😀 Cancel out any common terms between f(x + Δx) and f(x) to simplify the subtraction process.
- 😀 The remaining terms in the numerator after cancellation represent the change in the function.
- 😀 The next step is to divide the result by Δx, and then simplify the expression.
- 😀 The final step is to compute the limit as Δx approaches 0. If no terms involving Δx remain, the limit is simply the constant value left.
- 😀 In this specific example, the derivative of the function f(x) = 2x + 1 is 2, since after simplification, no Δx remains in the limit expression.
Q & A
What is the main topic of the video?
-The main topic of the video is calculating the derivative of a function using the method of increments, which is based on the definition of the derivative as a limit.
What is the formula for calculating the derivative in this video?
-The formula for the derivative is: f'(x) = lim(Δx → 0) [(f(x + Δx) - f(x)) / Δx].
How does the presenter simplify the derivative formula?
-The presenter simplifies the formula by applying it to a specific function f(x) = 2x + 1, and shows step-by-step how to calculate f(x + Δx) and cancel out common terms.
What is the first step in applying the formula?
-The first step is to calculate f(x + Δx) by substituting (x + Δx) into the function f(x). In this case, f(x) = 2x + 1, so f(x + Δx) becomes 2(x + Δx) + 1.
What happens after calculating f(x + Δx)?
-After calculating f(x + Δx), the next step is to subtract f(x) from f(x + Δx), cancel out the common terms (like 2x and +1), and simplify the expression.
What is the result after performing the subtraction of f(x + Δx) and f(x)?
-The result of the subtraction is 2Δx, which is the difference between f(x + Δx) and f(x) after canceling out the common terms.
What is the next step after getting the result of the subtraction?
-The next step is to divide the result of the subtraction (2Δx) by Δx, which gives 2. Then, the limit as Δx approaches 0 is calculated.
What does the limit of 2Δx / Δx as Δx approaches 0 yield?
-The limit of 2Δx / Δx as Δx approaches 0 simplifies to 2, because the Δx terms cancel out, leaving the constant 2.
What is the final result of the derivative calculation?
-The final result of the derivative calculation is 2, which is the value of f'(x), the derivative of f(x) = 2x + 1.
What example does the presenter give for viewers to practice after the video?
-The presenter gives the example of f(x) = 10x - 9 for viewers to calculate the derivative using the same method demonstrated in the video.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

01. Derivative using definition as limit

Definition of the Derivative
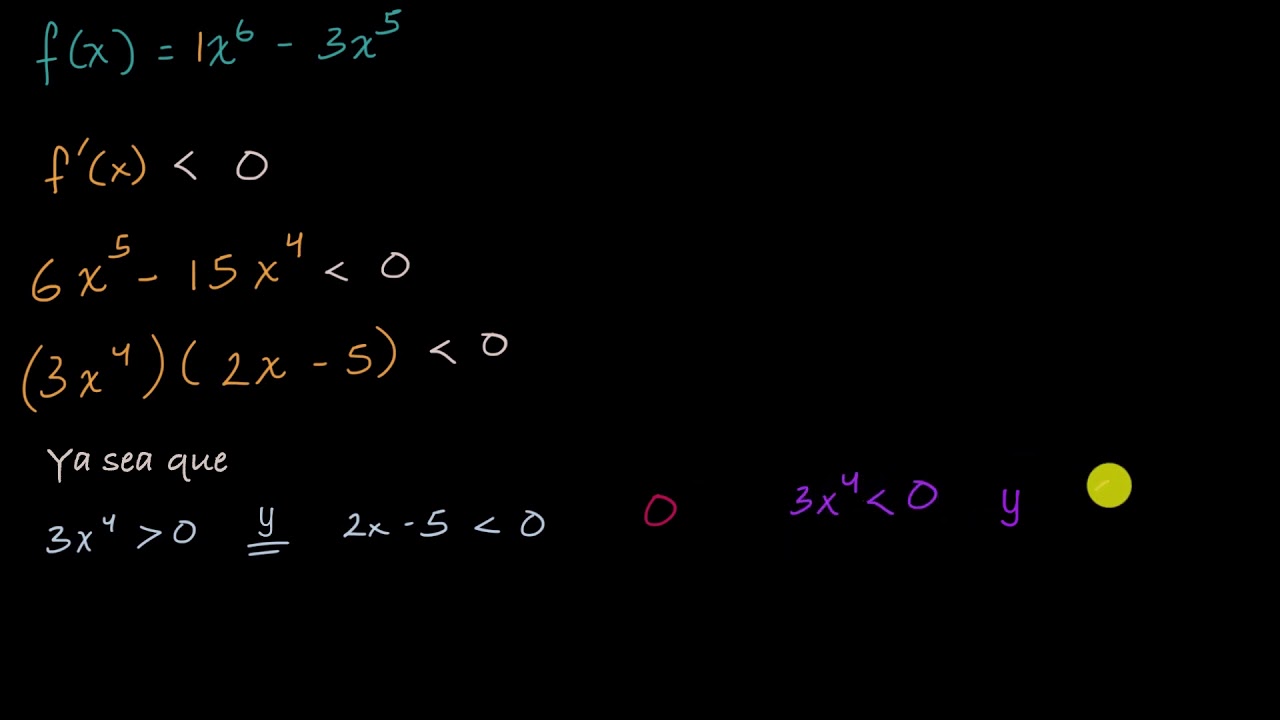
Encontrar el intervalo donde la función es decreciente | Cálculo

🟦 Máximos y Mínimos de una Función (Criterio de la Primer Derivada) | Video 3
Applying First Principles to x² (2 of 2: What do we discover?)

Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
