Deriving the t Distribution
Summary
TLDRThis video tutorial provides a comprehensive derivation of the T distribution, starting from the standard normal variable and the chi-squared variable. It explains the transformation of these variables to find the joint density of T and another variable, W, and details the integration process to obtain the marginal density of T. The video also discusses key properties of the T distribution, including its mean and variance, and visually compares PDFs for different degrees of freedom, illustrating how the distribution approaches the standard normal as degrees of freedom increase. Viewers are encouraged to engage with the content and subscribe for more insights.
Takeaways
- 😀 The T distribution is derived from the standard normal and chi-squared distributions.
- 😀 T is defined as the ratio of a standard normal variable Z to the square root of a chi-squared variable X divided by its degrees of freedom.
- 😀 The variables Z and X are assumed to be independent in this derivation.
- 😀 A new variable W is introduced to aid in the transformation process.
- 😀 The Jacobian of the transformation is crucial for deriving the joint density of T and W.
- 😀 The joint density of T and W is computed by substituting back transformed values for Z and X.
- 😀 The process includes simplifying the joint density to isolate W terms and constants.
- 😀 The marginal density of T is obtained by integrating out W from the joint density.
- 😀 The density function for T integrates to one and follows a specific gamma distribution structure.
- 😀 As the degrees of freedom increase, the T distribution approaches the standard normal distribution.
Q & A
What is the main focus of the video?
-The video focuses on deriving the T distribution from scratch using transformations of random variables.
What are the two variables involved in deriving the T distribution?
-The two variables are Z, a standard normal random variable, and X, a chi-squared random variable with n degrees of freedom.
What is the formula for T in the context of this video?
-T is defined as Z divided by the square root of X divided by its degrees of freedom, specifically T = Z / sqrt(X/n).
Why is it necessary to introduce the variable W in the derivation?
-W is introduced to help derive the joint density of T and W, allowing us to integrate out W to find the marginal density of T.
What mathematical concept is used to perform the transformation involving T and W?
-The Jacobian determinant is used to account for the transformation of variables when finding the joint density.
What does the joint density of T and W represent?
-The joint density of T and W represents the combined distribution of the two variables, which is derived from their individual probability density functions.
What is the significance of integrating out W?
-Integrating out W allows us to isolate and obtain the marginal density of T, which is essential for understanding the T distribution.
How does the degree of freedom affect the shape of the T distribution?
-As the degrees of freedom increase, the T distribution approaches a standard normal distribution, with thinner tails and a higher peak.
What are the conditions for the mean and variance of a T distribution?
-The mean of a T distribution is zero when n > 1, and the variance is n / (n - 2) when n > 2; it is infinite when 1 < n ≤ 2.
What visual comparisons are made regarding different degrees of freedom in the T distribution?
-The video illustrates that lower degrees of freedom result in fatter tails and shorter peaks, while higher degrees of freedom lead to thinner tails and taller peaks, converging to a normal distribution.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

What is the Chi-Squared distribution? Extensive video!

CONVERTING A NORMAL RANDOM VARIABLE TO A STANDARD NORMAL VARIABLE AND VICE VERSA
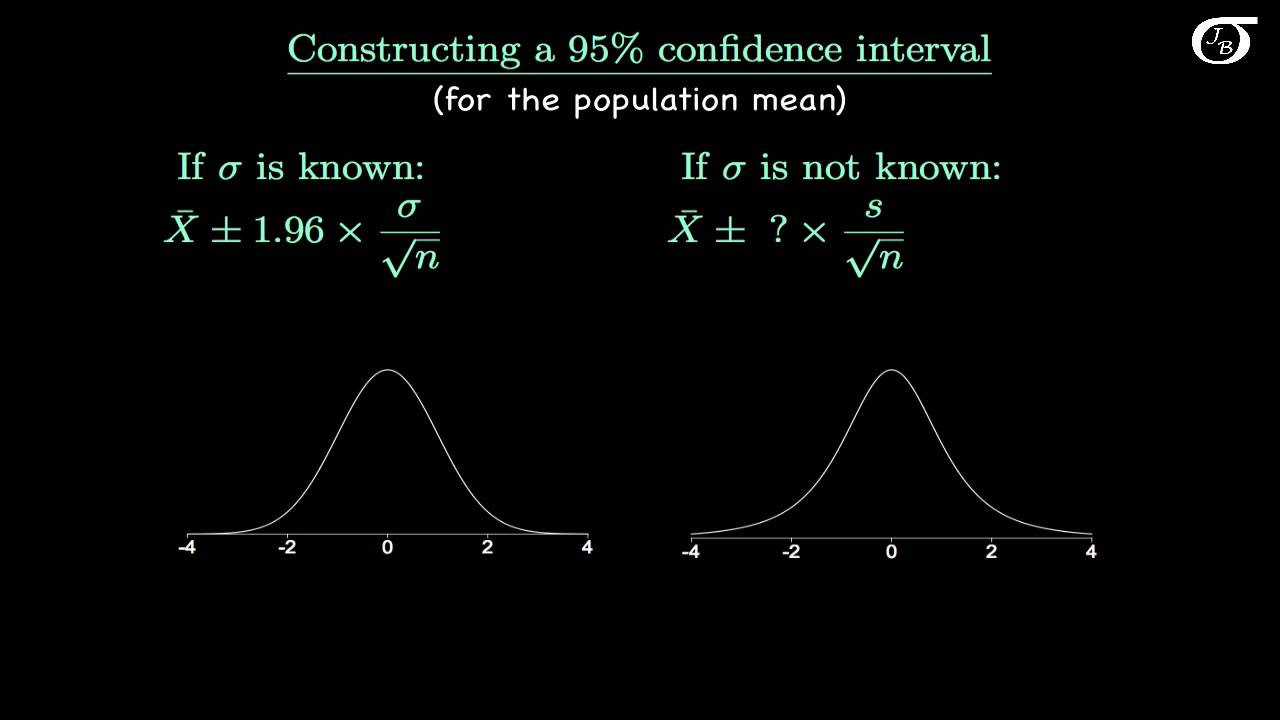
Introduction to the t Distribution (non-technical)

SPSS : Uji t, Uji F dan Koefisien Determinasi dalam Analisis Regresi Berganda
Uji t dan Uji F dalam Analisis Regresi Berganda dengan SPSS Lengkap

t-distribution in Statistics and Probability | Statistics Tutorial #9 | MarinStatsLectures
5.0 / 5 (0 votes)
