HPF RA S1 DTE ITS

Summary

The lecture discusses active and passive filters, focusing on low-pass and high-pass filters. It explains how capacitors and resistors are used in circuits to create these filters, emphasizing the role of operational amplifiers. The lecture covers the derivation of transfer functions and the relationship between frequency and gain in first and second-order filters. It also explores cutoff frequencies, phase angles, and the filter's response to various input frequencies. Practical examples of filter circuits and their calculations are provided to reinforce the theoretical concepts.

Takeaways

• 🔧 The script focuses on active and passive filters, specifically low-pass and high-pass filters.
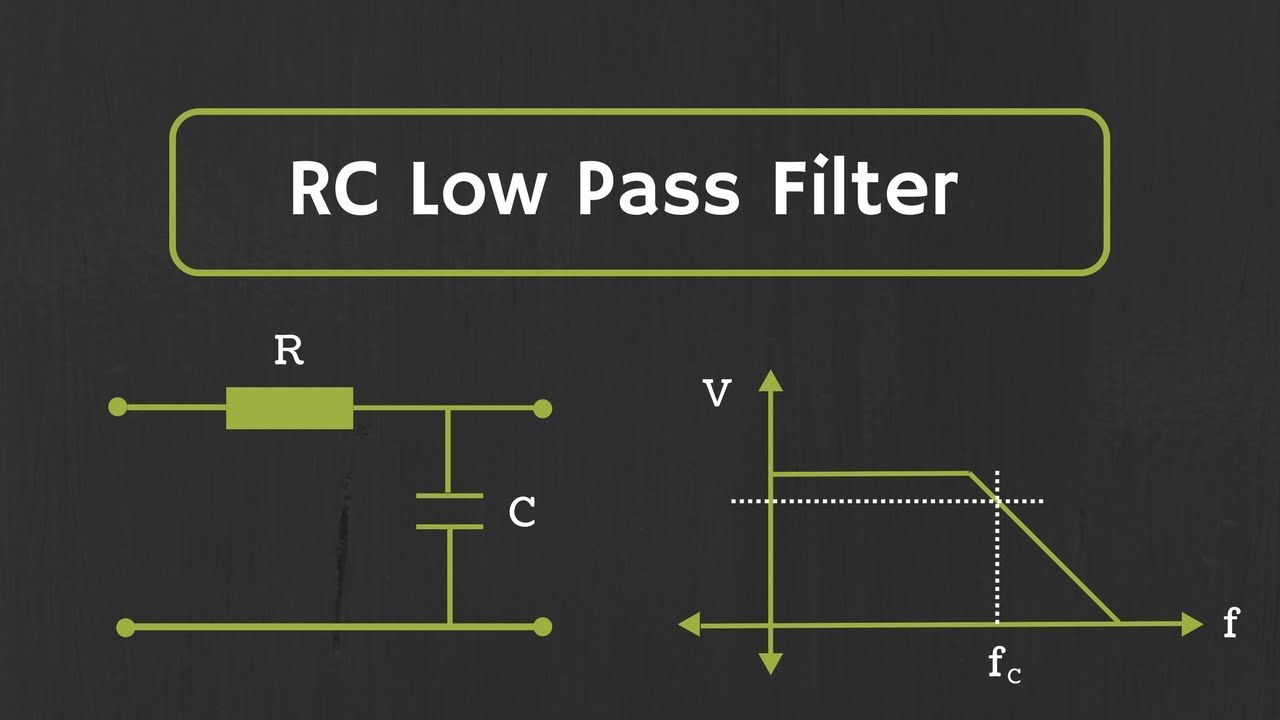
• 🌀 The low-pass filter design involves capacitors grounded, while in high-pass filters, capacitors are placed in front, with resistors connected to the output.
• 📉 High-pass filters allow high frequencies to pass while attenuating low frequencies, especially at low cut-off frequencies.
• 📐 The transfer function of the CR circuit is derived based on the frequency response, focusing on voltage division and resistor-capacitor relationships.
• ⚡ The script explains the impact of angular frequency (omega) on filter performance, especially how the cut-off frequency is determined.
• 🔄 First-order active filters exhibit a frequency response with 20 dB per decade change, while second-order filters show a steeper slope of 40 dB per decade.
• 📈 The gain response increases for high-pass filters with frequency, whereas low frequencies are dampened.
• 🔗 The role of operational amplifiers (OpAmps) is highlighted in active filter circuits, particularly as buffers or inverting amplifiers.
• 🔬 Practical calculations are presented for determining resistor and capacitor values to achieve specific cut-off frequencies in filter design.
• 📊 Graphical representation of the frequency response is discussed, illustrating how filters behave as frequency increases, stabilizing at certain levels.

Q & A

What is the basic principle behind the low-pass filter discussed in the script?

The low-pass filter discussed operates based on the principle of using a combination of capacitors and resistors, where the capacitor is connected to ground. It allows low-frequency signals to pass while attenuating high-frequency signals.

How is the transfer function of a passive CR circuit derived?

The transfer function is derived using a voltage divider formula, where the output voltage is calculated as a function of input voltage, capacitor, and resistor values. By simplifying the expression, the transfer function can be expressed in terms of frequency (Omega) and the circuit parameters.

What happens to the filter's behavior when the frequency is lower than the cut-off frequency?

When the frequency is lower than the cut-off frequency, the filter does not amplify the signal, and the output remains close to zero. The signal is heavily attenuated, especially at frequencies far below the cut-off point.

What is the significance of the cut-off frequency (fc) in a high-pass filter?

The cut-off frequency (fc) is the point at which the output signal starts to pass through the filter with minimal attenuation. For frequencies above fc, the signal is amplified or passed through, while frequencies below it are attenuated.

How is the phase shift of a high-pass filter calculated?

The phase shift of a high-pass filter is calculated using the formula for the inverse tangent (tan^(-1)) of the ratio of the operating frequency to the cut-off frequency. This gives the angle of phase shift, which is critical for understanding how the filter alters the phase of the input signal.

What is the effect of the filter on a signal when the frequency is much higher than the cut-off frequency?

When the frequency is much higher than the cut-off frequency, the filter passes the signal with minimal attenuation and the output remains relatively constant. The gain remains stable at a high level, reflecting the high-pass nature of the filter.

What is the meaning of 'gain per decade' in the context of filter design?

Gain per decade refers to the rate at which the gain of the filter increases or decreases with every tenfold increase in frequency. For example, in a first-order filter, the gain increases by 20 dB per decade in a high-pass filter and decreases by 20 dB per decade in a low-pass filter.

How does the filter configuration affect the gain in a high-pass filter?

The gain of a high-pass filter is determined by the configuration of the resistors and capacitors in the circuit. When the frequency is below the cut-off, the gain is low, and it increases as the frequency rises above the cut-off frequency.

What is the relationship between resistor and capacitor values in determining the cut-off frequency of a filter?

The cut-off frequency (fc) is inversely proportional to the product of the resistor (R) and capacitor (C) values in the filter. The formula is fc = 1 / (2πRC), meaning that increasing the resistor or capacitor values decreases the cut-off frequency and vice versa.

What is the significance of second-order filters compared to first-order filters?

Second-order filters provide a steeper roll-off compared to first-order filters. For instance, a first-order filter has a roll-off of 20 dB per decade, while a second-order filter has a roll-off of 40 dB per decade, making it more effective at attenuating undesired frequencies.