Electrical Engineering: Basic Laws (8 of 31) What Are Kirchhoff's Laws?
Summary
TLDRThis video introduces Kirchhoff's two fundamental laws for analyzing electrical circuits. The first law, Kirchhoff's Current Law (KCL), states that the sum of currents entering a node equals the sum of currents leaving it. The second law, Kirchhoff's Voltage Law (KVL), asserts that the sum of voltages around any closed loop in a circuit must equal zero. The video explains both concepts with examples of current and voltage flows, demonstrating how these principles apply to circuit analysis. Future videos will offer practical examples of using these laws to solve circuits.
Takeaways
- 🔌 Kirchhoff's First Law (KCL) states that the sum of currents entering a node equals the sum of currents leaving the node.
- 🔀 In a circuit, one current may enter a node, while two or more currents leave, and the sum of the outgoing currents equals the incoming one.
- 🚗 The analogy of cars entering and leaving an intersection is used to explain current flow in a node: the number of cars entering must equal the number leaving.
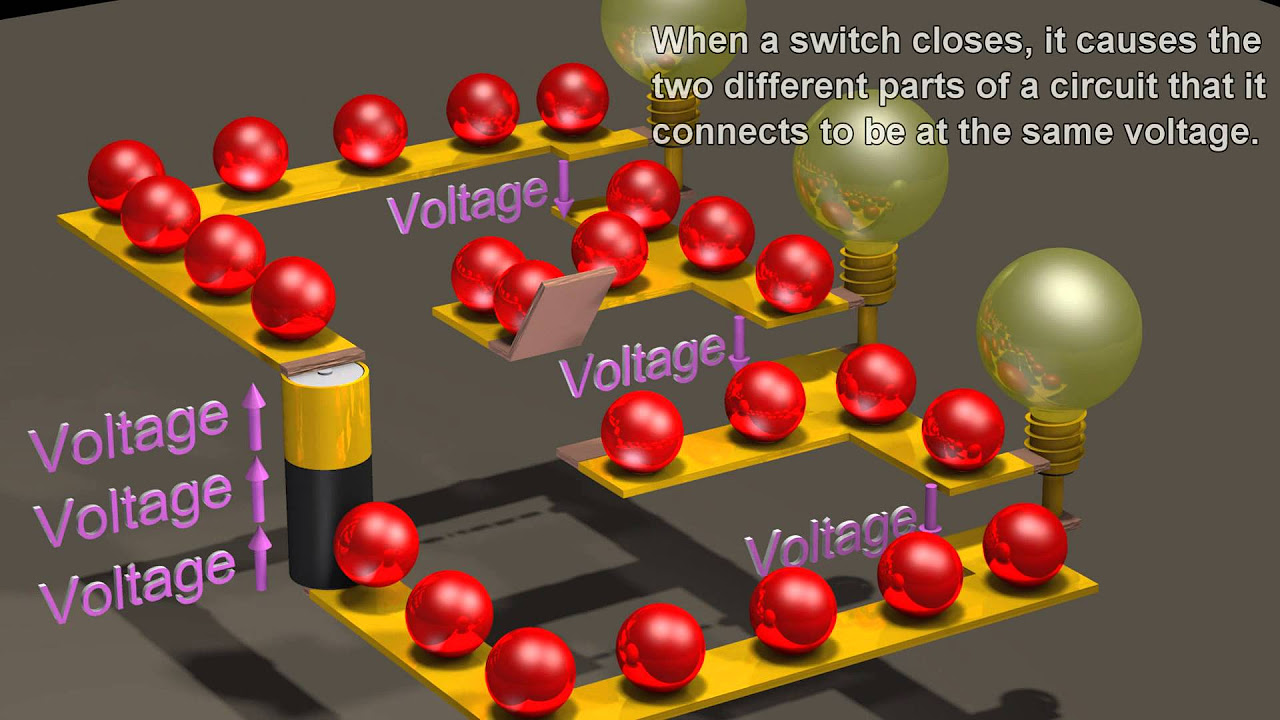
- 🔋 Kirchhoff's Second Law (KVL) states that in any closed loop, the sum of all voltages (voltage rises and drops) must equal zero.
- ⬆️ When moving across a battery from the negative to positive terminal, there's a positive voltage rise.
- 🔻 When current flows through a resistor in the same direction as the loop, it results in a voltage drop.
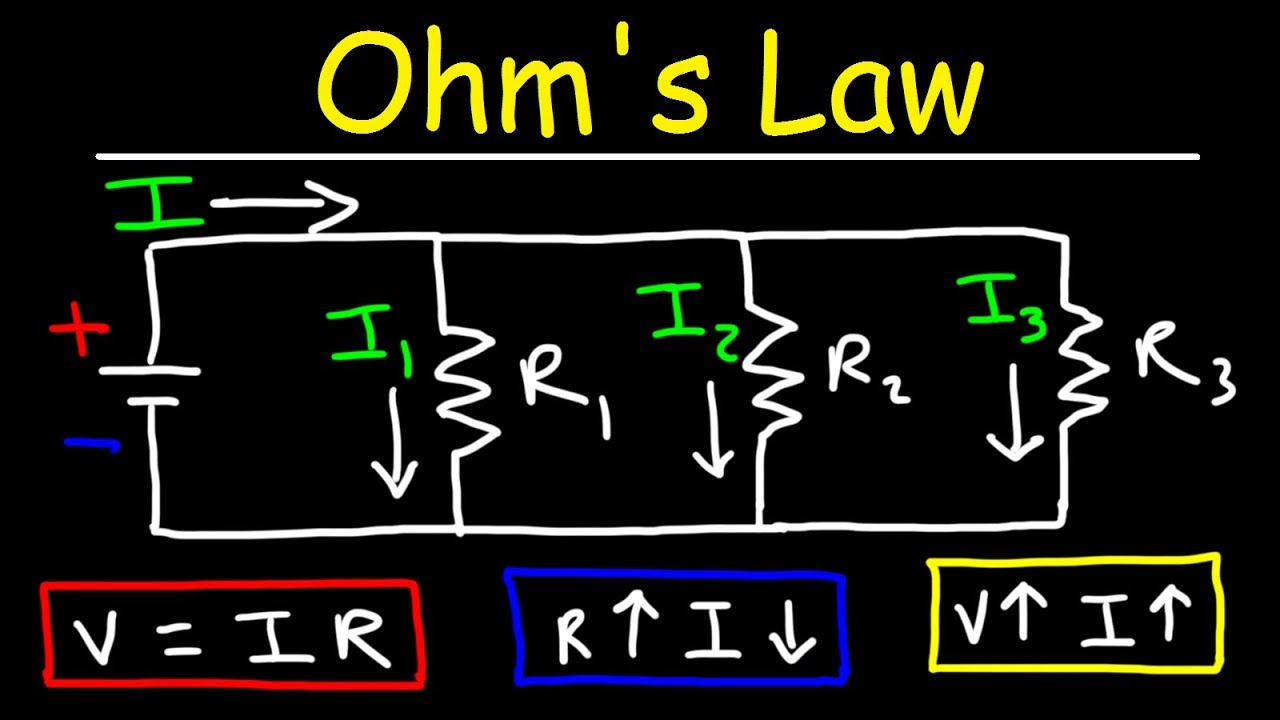
- 🔄 The voltage across a resistor is determined by the current through it and the resistor's resistance (Ohm's Law: V = IR).
- ⏩ The direction of travel in a loop relative to the current determines whether there is a voltage rise or drop across a resistor.
- 🔁 Traveling in the opposite direction of current through a resistor results in a voltage rise, not a drop.
- 💡 The two Kirchhoff laws (KCL and KVL) are essential tools for analyzing electrical circuits by balancing currents and voltages in nodes and loops.
Q & A
What is Kirchhoff's first law?
-Kirchhoff's first law, also known as the Current Law, states that for any node, the sum of all currents entering the node equals the sum of all currents leaving the node. This principle is based on the conservation of charge.
Can you provide an example of Kirchhoff's first law?
-In a circuit with three branches connected to a node, if current I1 enters the node and currents I2 and I3 leave the node, Kirchhoff's first law states that I1 = I2 + I3. This ensures that the total current entering the node equals the total current leaving it.
What analogy is used to explain Kirchhoff's first law?
-An analogy of cars at an intersection is used. The number of cars entering the intersection must equal the number of cars leaving, unless the cars disappear. Similarly, the currents entering and leaving a node must be equal.
What does Kirchhoff's second law state?
-Kirchhoff's second law, also known as the Voltage Law, states that for any closed loop in a circuit, the sum of all the voltages (voltage rises and voltage drops) must add up to zero. This is based on the conservation of energy.
How does the direction of current affect the voltage across a resistor?
-When traveling in the same direction as the current across a resistor, a voltage drop occurs, and it's considered negative. When traveling in the opposite direction of the current, a voltage rise occurs, and it's considered positive.
How do you calculate the voltage drop across a resistor?
-The voltage drop across a resistor is calculated using Ohm's Law, which is the current (I) in the circuit multiplied by the resistance (R) of the resistor, i.e., V = I * R.
What happens when you travel around a closed loop in a circuit?
-As you travel around a closed loop, the sum of all voltage rises and voltage drops must equal zero. This is in line with Kirchhoff's second law.
Why must the sum of voltages around a closed loop equal zero?
-The sum of voltages must equal zero because energy is conserved. As you move through the circuit, energy gained from sources (like batteries) must be equal to the energy lost across resistors or other components.
How do you handle voltage when traveling in the same direction as the current?
-When traveling in the same direction as the current, the voltage across a resistor is a drop, and this is counted as a negative value in Kirchhoff's voltage law.
What is the importance of understanding the direction of current in Kirchhoff's laws?
-Understanding the direction of current is crucial to applying Kirchhoff's laws correctly, especially when determining whether to add or subtract voltages in a loop and correctly interpreting current flows in and out of nodes.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)