ANGLES IN A UNIT CIRCLE || PRE-CALCULUS
Summary
TLDRThis educational video lesson delves into the concept of angles in a unit circle, explaining the geometric definition and its measurement in degrees. It covers the impact of direction of rotation on angle measurement, distinguishing between clockwise and counter-clockwise rotations. The video also instructs viewers on converting angle measures from decimal degrees to degrees, minutes, and seconds, and vice versa, using practical examples to clarify the process.
Takeaways
- 📐 Angles in a unit circle are discussed with a focus on geometry and trigonometry perspectives.
- 🔄 An angle is defined as the amount of rotation needed to move from the initial side to the terminal side.
- 👉 The direction of rotation affects angle measurement, with counter-clockwise being positive and clockwise being negative.
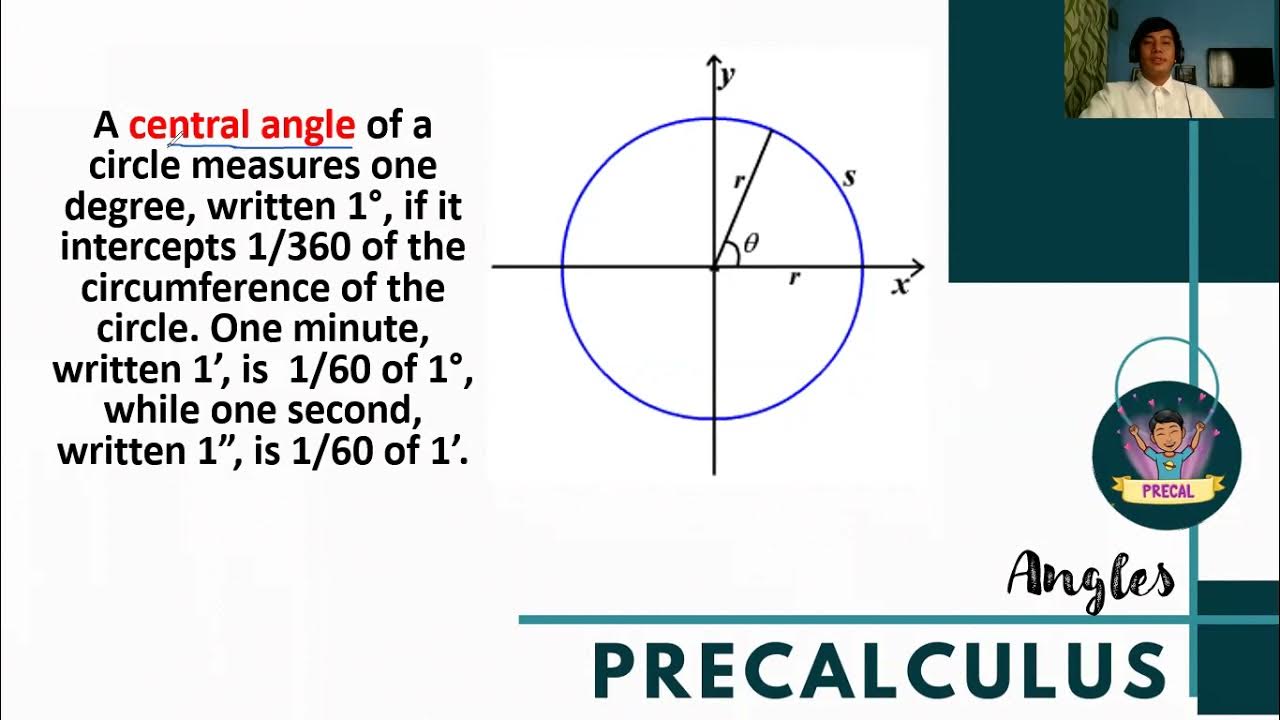
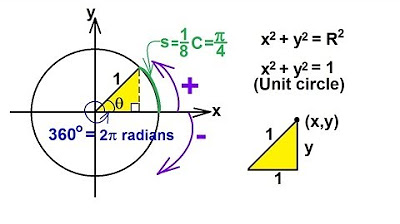
- 🌀 A full rotation (360 degrees) is equivalent to 0 degrees, illustrating the cyclical nature of angles.
- 🔢 The degree measure system, developed by Babylonians around 2000 BC, uses a sexagesimal (base-60) numeral system.
- ⏱️ One degree is equivalent to 60 minutes, and one minute is equivalent to 60 seconds.
- 📉 The script provides examples of converting decimal degrees to degrees, minutes, and seconds.
- 📈 It also demonstrates converting degrees, minutes, and seconds back to decimal degrees.
- 🔄 The process of converting between these units involves multiplying by 60 to go from degrees to minutes or from minutes to seconds.
- 📚 The tutorial is educational, aiming to teach viewers how to work with angles and their measurements.
- 🎓 The video concludes with a prompt for viewers to like, subscribe, and hit the bell button for more educational content.
Q & A
What is the definition of an angle in geometry?
-An angle is defined as the union of two non-collinear rays which have the same endpoint.
How does the definition of an angle in trigonometry differ from the geometric definition?
-In trigonometry, an angle is viewed as the amount of rotation generated when a ray is rotated about its endpoint, and it requires labeling the sides of the angle as initial and terminal.
What are the initial and terminal sides of an angle?
-The initial side is the position of the ray at the start, and the terminal side is the position of the ray at the end of its rotation.
How does the direction of rotation affect angle measures?
-Counter-clockwise rotation results in positive angle measures, while clockwise rotation results in negative angle measures.
What is the significance of a full rotation in terms of degrees?
-A full rotation is equivalent to 360 degrees.
How are degrees, minutes, and seconds related to each other in angle measurement?
-One degree is equal to 60 minutes, and one minute is equal to 60 seconds.
How can you convert a decimal degree measure to minutes and seconds?
-First, separate the whole number of degrees from the decimal. Then, multiply the decimal part by 60 to convert it to minutes. If there's a decimal in the minutes, multiply that decimal by 60 to convert it to seconds.
What is the final result when converting 22.4 degrees to degrees, minutes, and seconds?
-The final result is 22 degrees 24 minutes.
How do you convert 14.21 degrees to degrees, minutes, and seconds?
-First, convert the 0.21 degrees to minutes by multiplying by 60, resulting in 12.6 minutes. Then, take the decimal part of the minutes (0.6) and convert it to seconds by multiplying by 60, resulting in 36 seconds. The final answer is 14 degrees 12 minutes 36 seconds.
How can you convert a degree measurement in minutes and seconds to decimal degrees?
-Convert the minutes to a fraction of a degree by dividing by 60, and the seconds to a fraction of a degree by dividing by 3600 (60 seconds per minute and 60 minutes per degree). Then, add these fractions to the whole number of degrees.
What is the result when converting 31 degrees 12 minutes and 54 seconds to decimal degrees?
-First, convert the 54 seconds to minutes by dividing by 60, which gives 0.9 minutes. Then add this to the 12 minutes to get 12.9 minutes. Convert this to degrees by dividing by 60, which gives approximately 0.215 degrees. Add this to the 31 degrees to get a final result of approximately 31.215 degrees.
How is a negative angle measured in terms of degrees, minutes, and seconds?
-A negative angle is measured by converting the minutes and seconds to a decimal form and then subtracting that from the degrees. For example, -5 degrees 48 minutes 41 seconds is converted to -5.81 degrees by first converting 41 seconds to 0.68 minutes and then adding that to 48 minutes to get 48.68 minutes, which is then converted to 0.81 degrees and subtracted from -5 degrees.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)