Integración por fracciones parciales | Los cuatro casos Introducción
Summary
TLDREste vídeo ofrece una introducción a las integrales por fracciones parciales, enfocándose en el caso donde el grado del numerador es menor que el del denominador. Se explica la importancia de la factorización en la resolución de integrales y se presentan cuatro posibles respuestas dependiendo de los factores lineales y cuadráticos irreducibles del denominador. El vídeo invita a los espectadores a repasar la factorización y a explorar más ejemplos en futuras lecciones.
Takeaways
- 📚 Este video es una introducción a las integrales por fracciones parciales.
- 🔢 Se enfatiza que el grado del numerador debe ser menor que el del denominador para usar fracciones parciales.
- 🎓 Se explica que el grado del denominador se determina por el exponente máximo de x en la fracción.
- 📐 Se menciona que si el grado del numerador es mayor, se requiere una división antes de aplicar fracciones parciales.
- 📘 Se destaca la importancia de la factorización del denominador para resolver integrales de este tipo.
- 🔄 Se menciona que los factores pueden ser lineales o cuadráticos irreducibles y que deben diferenciarse.
- 🔢 Se describe que los factores lineales son aquellos donde x está elevado a la primera potencia.
- 🔄 Se indica que los factores cuadráticos irreducibles son trinomios de la forma x^2 + n, donde n es un número.
- 📝 Se sugiere revisar el curso de factorización si el espectador no está familiarizado con el proceso.
- 👨🏫 Se invita a los espectadores a suscribirse, comentar, compartir y dar like al vídeo si les gustó el contenido.
Q & A
¿Qué es una integral por fracciones parciales?
-Una integral por fracciones parciales es una técnica para integrar funciones racionales, es decir, fracciones donde tanto el numerador como el denominador son polinomios. Consiste en descomponer la fracción en una suma de fracciones más simples que pueden integrarse fácilmente.
¿Cuándo se dice que el grado del numerador es menor que el grado del denominador?
-El grado del numerador es menor que el grado del denominador cuando el exponente máximo del numerador es menor que el exponente máximo del denominador en la fracción.
¿Qué sucede si el grado del numerador es mayor que el grado del denominador?
-Si el grado del numerador es mayor que el grado del denominador, la integral puede resolverse mediante la división del numerador entre el denominador y luego integrar la fracción resultante.
¿Por qué es importante factorizar el denominador en integrales por fracciones parciales?
-Es importante factorizar el denominador para poder identificar el tipo de fracción parcial que se va a usar y para poder aplicar las técnicas de integración adecuadas. Además, permite observar qué tipo de solución se va a realizar.
¿Cuáles son los cuatro tipos de factores que pueden aparecer en el denominador de una fracción racional?
-Los cuatro tipos de factores son: 1) Factores lineales diferentes, 2) Factores lineales que se repiten, 3) Factores cuadráticos irreducibles que no se repiten y 4) Factores cuadráticos irreducibles que se repiten.
¿Qué son los factores lineales?
-Los factores lineales son aquellos donde el exponente de la variable es 1, es decir, el factor tiene la forma x^1.
¿Cómo se reconocen los factores cuadráticos irreducibles?
-Los factores cuadráticos irreducibles se reconocen porque están en la forma x^2 + n, donde n es un número, y no se pueden factorizar más.
¿Qué significa que un factor cuadrático se repita en el denominador?
-Un factor cuadrático se repite si aparece más de una vez en el denominador elevado a una potencia. Por ejemplo, (x^2 + 4)^2 significa que el factor cuadrático x^2 + 4 se repite dos veces.
¿Cuál es la estrategia para factorizar un trinomio de la forma x^2 + bx + c?
-Para factorizar un trinomio de la forma x^2 + bx + c, se puede utilizar la división sintética o buscar dos números que multipliados den c y sumados den b.
¿Por qué es útil conocer las técnicas de factorización en integrales por fracciones parciales?
-Conocer las técnicas de factorización es útil porque permite simplificar el denominador y, por ende, facilitar el proceso de integración por fracciones parciales.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

¿Cómo identificar a que tipo de fracciones parciales corresponde una integral?
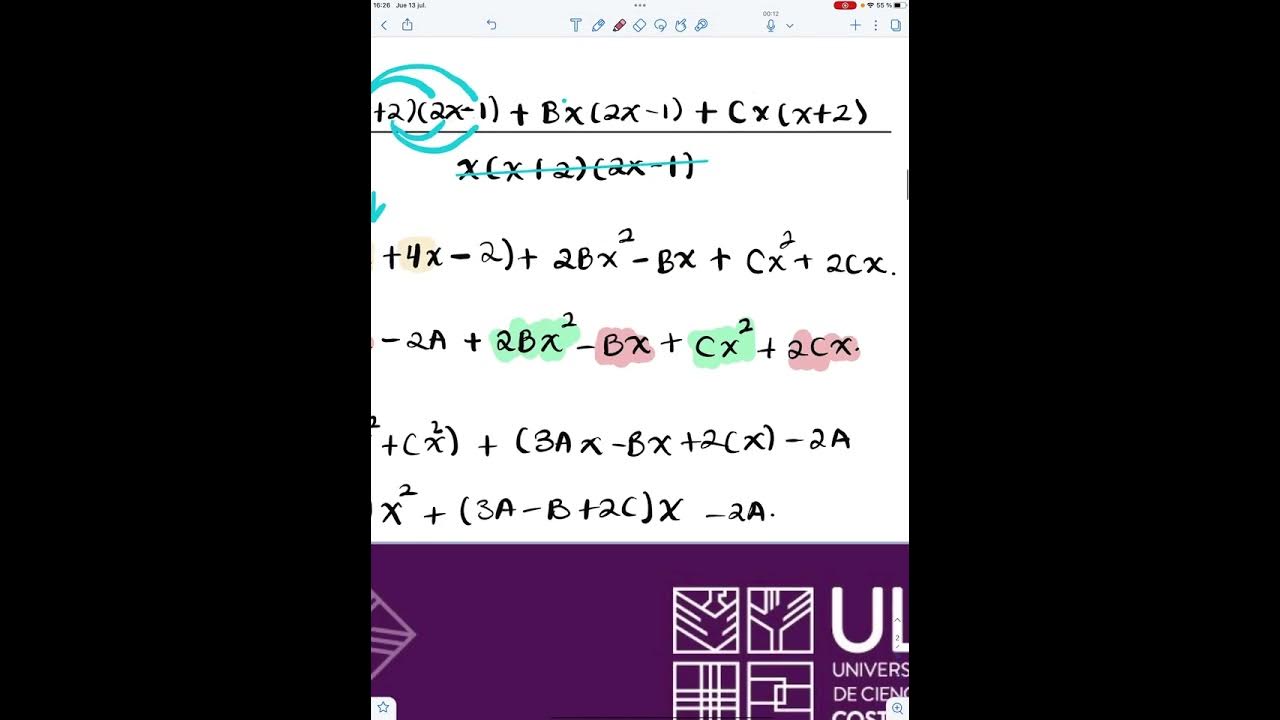
Fracciones parciales caso 1

Asíntotas verticales, horizontales y oblicuas de una función racional

Integral por descomposición en fracciones simples, integrales racionales

resta de fracciones

Racionalización de denominadores (CASO 2)
5.0 / 5 (0 votes)
