DIVISION OF POLYNOMIALS USING LONG DIVISION || GRADE 10 MATHEMATICS Q1
Summary
TLDRThis instructional video script outlines the process of dividing polynomials using long division. It guides viewers through each step, starting with arranging polynomials by decreasing exponents and inserting zeros for missing terms. The tutorial demonstrates dividing the first term, multiplying the partial quotient by the divisor, subtracting from the dividend, and repeating until complete. Examples are provided, including dividing \(x^3 - 4x^2 + 3x - 6\) by \(x - 2\), and \(3x^5 + 3x^4 - x^3 + 3x^2\) by \(x^2 + 1\), with each step explained in detail. The script concludes with a prompt to like, subscribe, and stay updated for more educational content.
Takeaways
- 📚 Long division is a method used to divide polynomials.
- 🔢 The process involves arranging the dividend and divisor in decreasing order of exponents, and inserting zeros where necessary.
- ✅ Begin by dividing the first term of the dividend by the first term of the divisor.
- 🔄 Multiply the partial quotient by the divisor and subtract the result from the dividend.
- 🔽 Bring down the next term in the dividend and repeat the process until all terms have been processed.
- 📉 An example given in the script is dividing x^3 - 4x^2 + 3x - 6 by x - 2.
- 🔗 Each step in the division process is explained with a focus on exponents and coefficients.
- 📈 The script demonstrates how to handle negative terms and remainders in polynomial division.
- 📝 The final answer includes the quotient and the remainder, if any.
- 🎓 The video aims to educate viewers on polynomial division, encouraging practice and further learning.
- 👍 The presenter invites viewers to like, subscribe, and stay updated for more educational content.
Q & A
What is the first step in polynomial long division?
-The first step is to arrange the dividend and divisor in decreasing power of exponents and insert zeros as coefficients for missing terms if necessary.
How do you divide the first term of the dividend by the first term of the divisor?
-You divide the highest power term of the dividend by the highest power term of the divisor using exponent subtraction. For example, in the division of x^3 by x, the result is x^2.
What do you do after dividing the first terms in polynomial long division?
-After dividing, you multiply the partial quotient by the entire divisor, and then subtract the result from the dividend.
Why is it important to subtract the results carefully in polynomial long division?
-Subtracting the results carefully is essential because any miscalculation will affect the accuracy of the remaining steps. It ensures that the new dividend is correct for the next step.
What happens if you encounter a missing term during polynomial division?
-If a term is missing in the polynomial, you must insert a zero as its coefficient to maintain consistency in the process of long division.
How do you handle remainders in polynomial long division?
-The remainder, if any, is expressed as a fraction with the remainder divided by the original divisor. For example, if the remainder is -8 and the divisor is x - 2, the remainder is written as -8/(x - 2).
What is the result of dividing x^3 - 4x^2 + 3x - 6 by x - 2?
-The quotient is x^2 - 2x - 1, and the remainder is -8. The final answer is x^2 - 2x - 1 + (-8)/(x - 2).
What does 'bring down the next term' mean in polynomial division?
-After each subtraction step, you bring down the next term from the dividend and continue the division process until all terms have been processed.
Why do you subtract the exponents when dividing terms in polynomial long division?
-You subtract the exponents because of the rules of exponents. When dividing like terms, you subtract the exponent of the divisor from the exponent of the dividend.
How do you handle division when the divisor has multiple terms, such as in 'divide by x^2 + 1'?
-In this case, you divide the first term of the dividend by the first term of the divisor, perform the multiplication of the quotient by the entire divisor, and continue the division process with the remaining terms.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Long Division With Polynomials - The Easy Way!
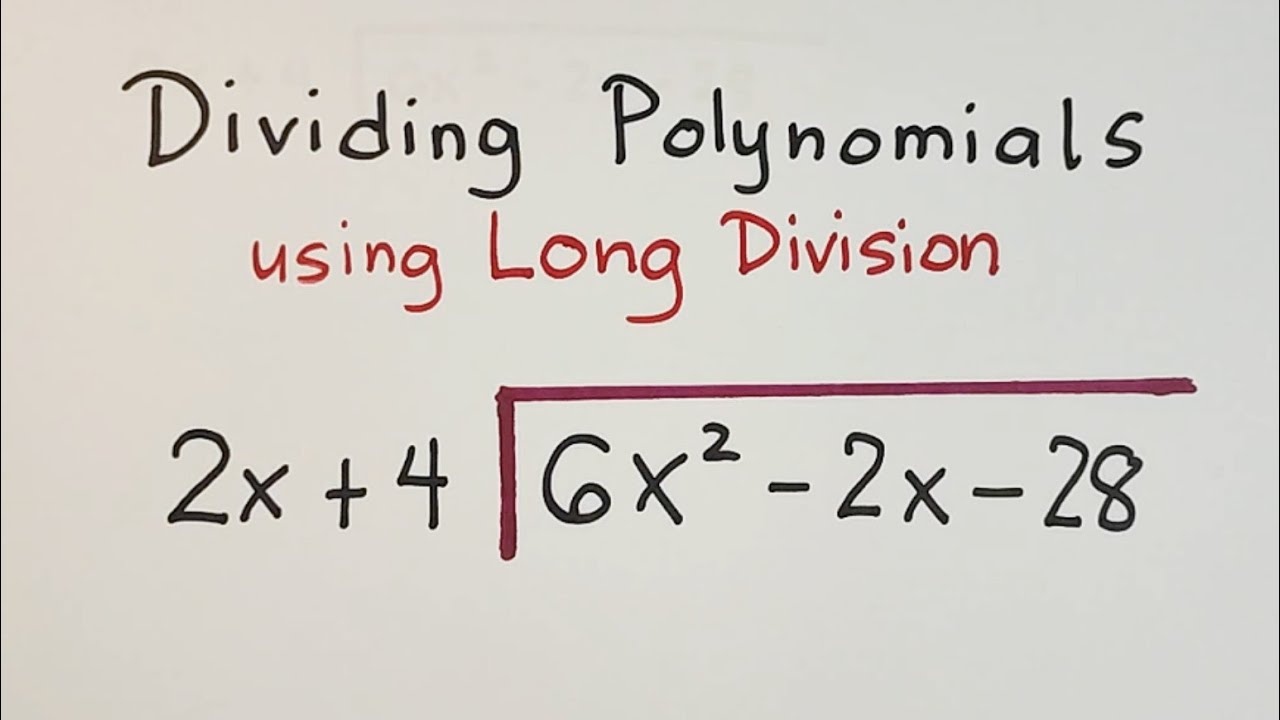
How to Divide Polynomials using Long Division - Polynomials

TAGALOG: Division of Polynomials - Long Division and Synthetic Division #TeacherA

How to Divide Polynomials Using LONG DIVISION | Math 10

Long Division | How to Divide Polynomials | Grade 10 Math @MathTeacherGon
Polynomials - Adding, Subtracting, Multiplying and Dividing Algebraic Expressions
5.0 / 5 (0 votes)
