CONVERTIR de BINARIO a DECIMAL - Ejercicio #5
Summary
TLDREn este video se explica cómo convertir un número binario a decimal. Se sigue un proceso paso a paso: primero se enumeran los dígitos del número binario, luego se crea una tabla de potencias de 2 hasta el último dígito. A continuación, se asigna a cada dígito su correspondiente valor de potencia de 2, y finalmente, se realiza la suma de los valores donde se tiene un 1. El ejemplo dado es el número binario '1010011', que al aplicar el proceso se traduce a 83 en sistema decimal. El video termina con una invitación a ver más contenido relacionado.
Takeaways
- 📚 Aprender a convertir números binarios a decimales es el objetivo del video.
- 👉 El número binario dado es 1 0 1 0 0 1 1.
- 🔢 Se comienza enumerando los dígitos del número binario, empezando por la derecha.
- 📊 Se crea una tabla de potencias de 2, que varía desde 2^0 hasta 2^6.
- ✅ 2^0 es 1, 2^1 es 2, y así sucesivamente hasta 2^6 que es 64.
- 📝 Se asigna a cada dígito de la izquierda su correspondiente valor de potencia de 2.
- 🔄 Se realiza la suma de los productos de cada dígito y su valor correspondiente.
- 🚫 Los ceros no afectan la suma ya que multiplicados por cualquier número dan cero.
- 🔢 Solo se suman los valores donde hay un 1 en el número binario.
- 💡 La suma final es 64 + 16 + 2 + 1, que da un total de 83.
- 🔢 El número binario 1 0 1 0 0 1 1 equivale al número decimal 83.
- 👋 El video concluye con una invitación a ver más contenido relacionado.
Q & A
¿Qué es el sistema binario y cómo se relaciona con el sistema decimal?
-El sistema binario es un sistema numérico que utiliza solo dos dígitos: 0 y 1. Se relaciona con el sistema decimal porque es una forma de representar números, pero mientras que el decimal es base 10, el binario es base 2.
¿Cuál es el primer paso para convertir un número binario a decimal según el guion?
-El primer paso es enumerar todos los dígitos del número binario, iniciando desde la derecha a la izquierda, comenzando en 0.
¿Cómo se realiza la tabla de potencias del número 2 en el proceso de conversión binaria a decimal?
-Se crea una tabla que incluye las potencias de 2, comenzando en 2^0 y aumentando su exponente hasta el último dígito enumerado del número binario.
¿Cuál es el valor de 2^0 y cómo se utiliza en la conversión binaria a decimal?
-El valor de 2^0 es 1, y se utiliza multiplicando este valor por el dígito binario correspondiente en la posición que se está evaluando.
¿Cómo se determina el valor que corresponde a cada dígito en el número binario durante la conversión a decimal?
-Se multiplica el valor de la potencia de 2 correspondiente por el dígito binario (0 o 1) que se encuentra en esa posición.
¿Por qué solo se suman los productos donde hay un 1 en el número binario?
-Solo se suman los productos donde hay un 1 porque el 0 multiplicado por cualquier número da 0, por lo que no contribuye a la suma final.
¿Cuál es el resultado de la suma en el ejemplo del guion tras convertir el número binario 1 0 1 0 0 1 1 a decimal?
-El resultado de la suma es 83, que es el valor decimal del número binario 1 0 1 0 0 1 1.
¿Cómo se puede simplificar el proceso de conversión binaria a decimal si se conoce la posición de los dígitos?
-Se puede simplificar recordando que cada posición representa una potencia de 2 y sumando solo los valores de las posiciones con un 1.
¿Qué ocurre si el número binario tiene más de 7 dígitos en el ejemplo proporcionado?
-Si el número binario tiene más de 7 dígitos, se continuaría creando potencias de 2 hasta el último dígito y se seguiría el mismo proceso de multiplicación y suma.
¿Cómo se pueden aplicar los conceptos aprendidos en el video para convertir números binarios más largos o más cortos a decimal?
-Los mismos pasos se aplican, pero se crea una tabla de potencias de 2 hasta el último dígito del número binario, y se realizan las multiplicaciones y sumas correspondientes.
¿Por qué es útil aprender a convertir números del sistema binario al sistema decimal?
-Es útil porque el sistema binario es la base de la computación y la electrónica moderna, y la habilidad para convertir entre sistemas numéricos ayuda a entender y trabajar con tecnología.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Convertidor Binario a Decimal LabVIEW Parte 1

CONVERTIR UN NÚMERO DECIMAL A BINARIO - Super facil - Para principiantes
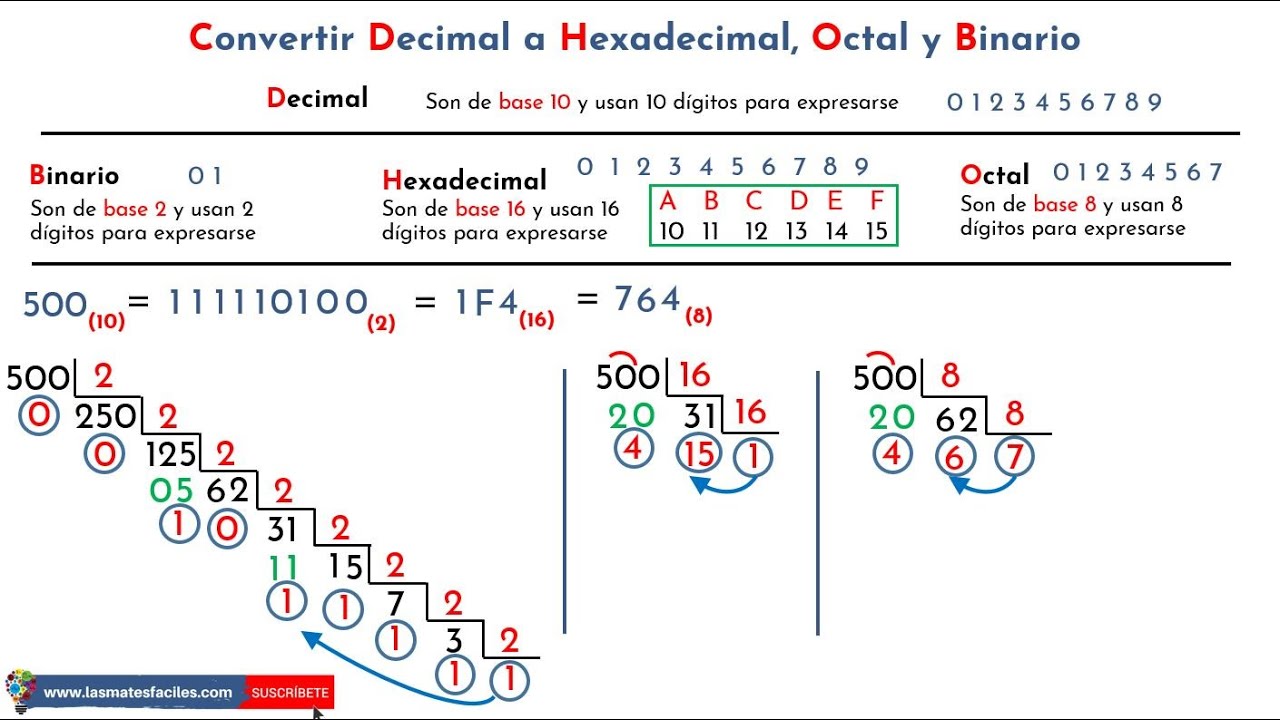
Convertir: Decimal a Binario - Decimal a Hexadecimal - Decimal a Octal - Ejemplos paso a paso!

Convertir Binario a Decimal
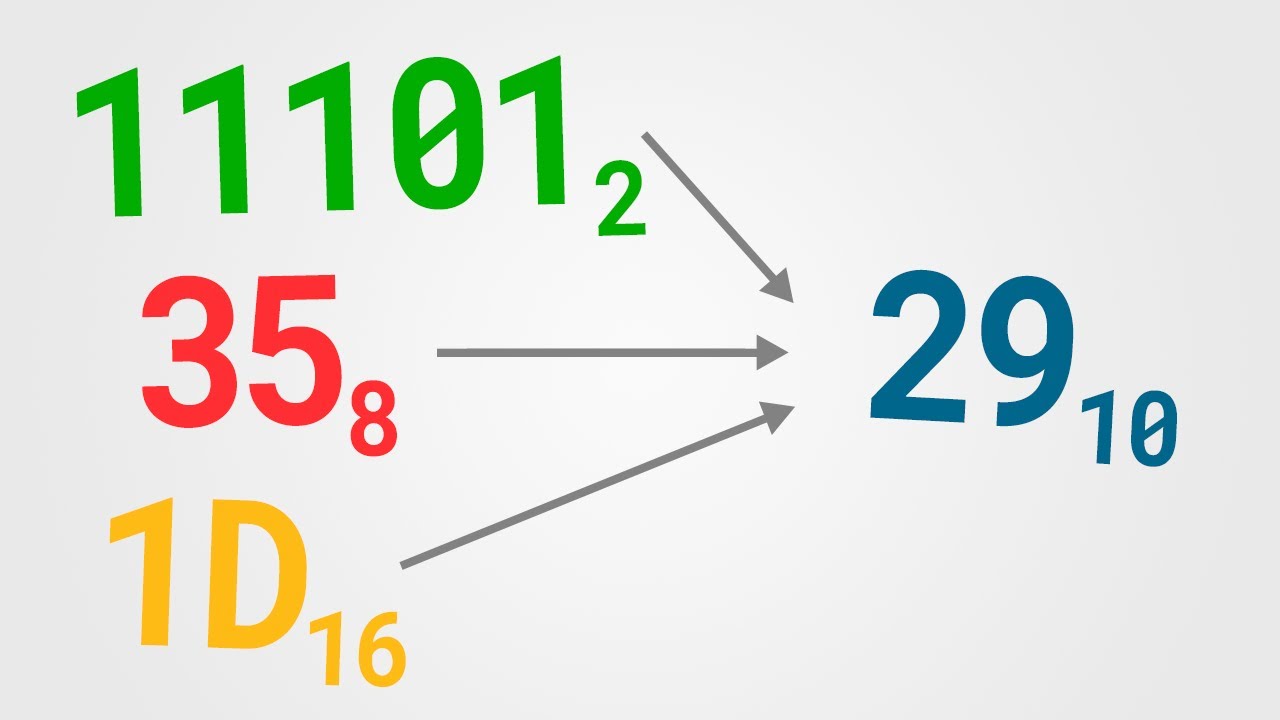
Conversiones entre sistemas de numeración (Binario, octal y hexadecimal a decimal)

Pasar de Notación Científica a Decimal | Ejemplo 1
5.0 / 5 (0 votes)
