Statistics-Left Skewed And Right Skewed Distribution And Relation With Mean, Median And Mode

Summary

In this informative video, Krishnak discusses common examples of right and left skewed distributions, such as wealth distribution and human lifespan, and explains their characteristics. He also clarifies the relationship between mean, median, and mode in these distributions, noting that in right skew, mean > median > mode, while in symmetrical distributions like normal distribution, mean ≈ median ≈ mode, and in left skew, mode > median > mean. Krishnak emphasizes the importance of practical knowledge for better understanding and explanation of these concepts.

Takeaways

• 📚 The video discusses a statistical question related to skewness in data distributions that was asked in an interview.
• 📈 The script explains the concept of right skew distribution, where the right tail of the data distribution is elongated, compared to the left.
• 💰 Wealth distribution is given as a classic example of a right skew distribution, highlighting the few extremely wealthy individuals compared to the majority with less wealth.
• ✍️ The length of comments on the speaker's YouTube channel is used as another example of a right skew distribution.
• 📊 The script contrasts right skew distribution with symmetrical (normal) distribution, which includes examples like age, weight, and height distributions.
• 🌟 Machine learning algorithms often prefer data that follows a normal distribution, as it simplifies the modeling process.
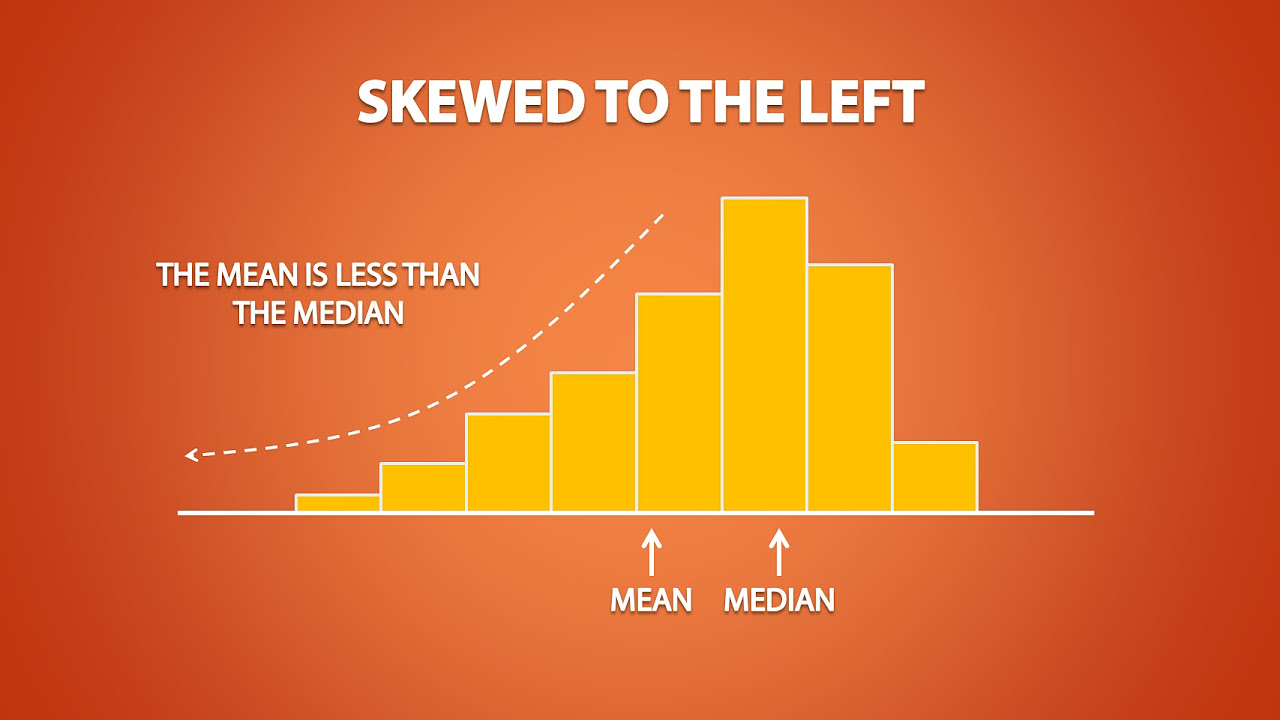
• 🔄 The left skew (or negative skew) distribution is also explained, with the lifespan of humans given as an example, where few live much longer than the average lifespan.
• 🔢 In a right skewed distribution, the mean is greater than the median, which in turn is greater than the mode.
• ⚖️ For symmetrical distributions, the mean, median, and mode are approximately equal, reflecting the balance of the data.
• 📉 In left skewed distributions, the mode is the highest, followed by the median, and then the mean, indicating the concentration of data towards the lower end.
• 🤓 The importance of understanding and being able to explain theoretical concepts with practical examples is emphasized for effective communication in interviews.

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is the concept of right skew distribution and left skew distribution, along with examples and the relationship between mean, median, and mode in these distributions.

What is a right skew distribution?

A right skew distribution, also known as a positively skewed distribution, is a type of distribution where the tail on the right side is longer or fatter than the left side, indicating that the data has a longer tail to the right.

Can you provide an example of a right skew distribution mentioned in the video?

One example of a right skew distribution mentioned in the video is wealth distribution, where a few extremely wealthy individuals like Elon Musk and Jeff Bezos represent the long tail on the right side of the distribution.

What is a left skew distribution?

A left skew distribution, also known as a negatively skewed distribution, is a type of distribution where the tail on the left side is longer or fatter than the right side, indicating that the data has a longer tail to the left.

Can you provide an example of a left skew distribution mentioned in the video?

The lifespan of human beings is given as an example of a left skew distribution, where there are fewer people living to very old ages compared to the average lifespan, creating a longer tail on the left side.

What is the relationship between the mean, median, and mode in a right skew distribution?

In a right skew distribution, the mean is greater than the median, and the median is greater than the mode. This is because the long tail on the right side pulls the mean to a higher value than the median.

What is the relationship between the mean, median, and mode in a left skew distribution?

In a left skew distribution, the mode is the highest, followed by the median, and then the mean. This is because the long tail on the left side pulls the mean to a lower value than the mode.

What is a symmetrical distribution and what is an example mentioned in the video?

A symmetrical distribution is one where the right and left sides of the distribution are mirror images of each other. An example mentioned in the video is the normal distribution, which is often seen in features like age, weight, and height in datasets.

What is the relationship between the mean, median, and mode in a symmetrical distribution?

In a symmetrical distribution, the mean, median, and mode are approximately equal, as the distribution is balanced with no skew to either side.

Why is it important to understand the relationship between mean, median, and mode in different types of distributions?

Understanding the relationship between mean, median, and mode in different distributions is important because it helps in interpreting the data correctly. It can indicate the presence of outliers, the central tendency, and the skewness of the data, which are crucial for data analysis and decision-making.

How can one remember the relationship between mean, median, and mode in different distributions?

One can remember the relationship by visualizing the distribution diagrams and associating the positions of mean, median, and mode with the direction of the skew. For right skew, mean > median > mode; for symmetrical, mean ≈ median ≈ mode; for left skew, mode > median > mean.