Radius & diameter from circumference | High School Geometry | High School Math | Khan Academy
Summary
TLDRThis educational video explains how to determine the radius and diameter of a circle given its circumference. It uses the formula C = 2πr to show that if the circumference is 49π, the radius is 24.5 units. Similarly, if the circumference is 1600π, the diameter is 1600 units, highlighting the fundamental role of pi in these calculations.
Takeaways
- 📏 The circumference of a circle is given as 49 pi, and the task is to find the radius.
- 🔍 A circle is drawn to visualize the problem, emphasizing the relationship between the radius and the circumference.
- 📐 The formula for the circumference of a circle is 2πr, where r is the radius.
- 🔢 Pi (π) is defined as the ratio of the circumference to the diameter of a circle.
- 🔍 The diameter of a circle is twice the radius (2r), and thus the circumference is π × 2r.
- 🔧 To solve for the radius, substitute the given circumference (49 pi) into the formula and solve for r.
- 🧩 After substituting, the equation becomes 49π = 2πr, and dividing both sides by 2π gives r = 24.5.
- 🌐 Another example is given with a circumference of 1600 pi, and the task is to find the diameter.
- 🔗 The relationship between the circumference and the diameter is used again, with the formula C = πD, where C is the circumference and D is the diameter.
- 📉 By dividing 1600 pi by pi, the diameter is found to be 1600 units, assuming the units are consistent.
- 🌟 Circles and the concept of pi are highlighted as fundamental and recurring in mathematics.
Q & A
What is the given circumference of the first circle mentioned in the transcript?
-The given circumference of the first circle is 49 pi.
How is the circumference of a circle related to its radius?
-The circumference of a circle is equal to two pi times the radius (C = 2πr).
What equation is used to find the radius when the circumference is known?
-The equation used is C = 2πr. By substituting the known circumference, we can solve for the radius.
How is the radius calculated from the given circumference of 49 pi?
-By setting 49 pi equal to 2πr and dividing both sides by 2π, the radius is found to be 24.5 units.
What is the diameter of a circle in terms of its radius?
-The diameter of a circle is twice the radius (d = 2r).
What is the given circumference of the second circle mentioned in the transcript?
-The given circumference of the second circle is 1600 pi.
How is the circumference related to the diameter?
-The circumference is equal to pi times the diameter (C = πd).
What equation is used to find the diameter when the circumference is known?
-The equation used is C = πd. By substituting the known circumference, we can solve for the diameter.
How is the diameter calculated from the given circumference of 1600 pi?
-By setting 1600 pi equal to πd and dividing both sides by π, the diameter is found to be 1600 units.
Why is the number pi significant in the context of circles?
-The number pi is significant because it is the ratio between the circumference and the diameter of a circle, a fundamental constant in mathematics.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

How to Calculate Circumference of a Circle (Step by Step) | Circumference Formula
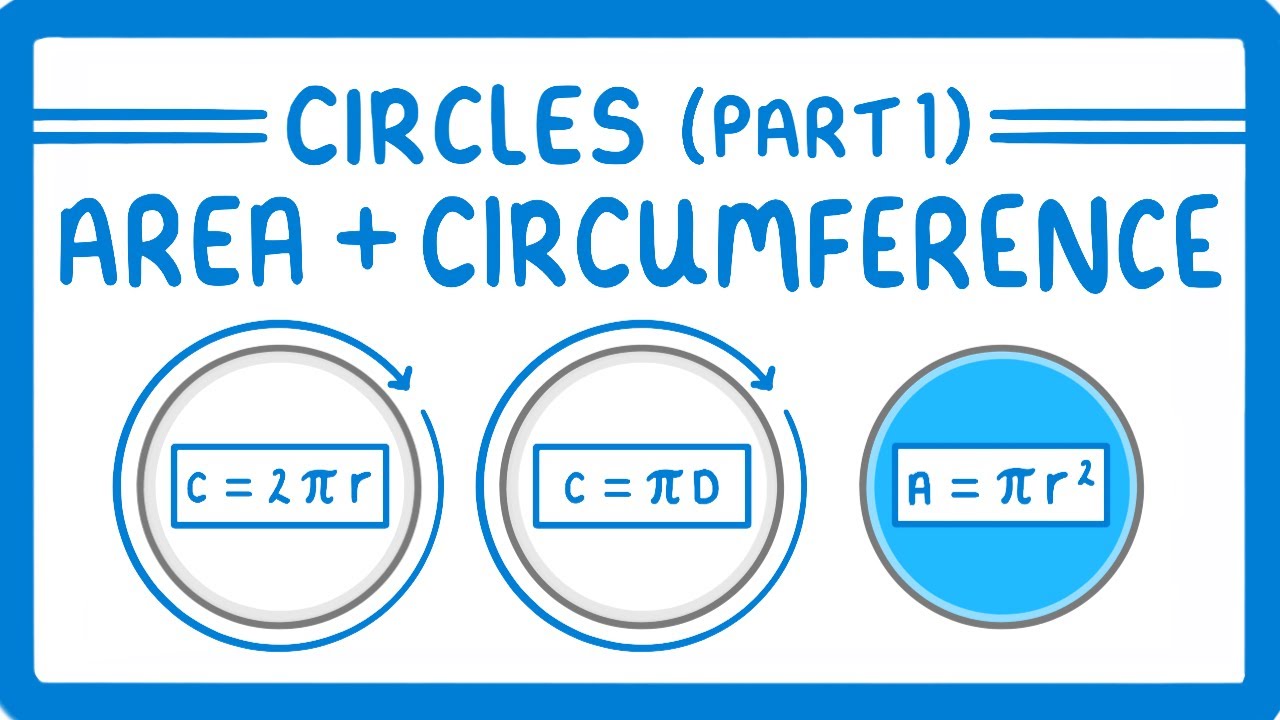
GCSE Maths - How to find the Area and Circumference of a Circle (Circles Part 1) #106

Cara Mencari Keliling dan Luas Lingkaran Jika Jari-jari dan Diameter Diketahui

Lingkaran dan Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka

Review on Circles
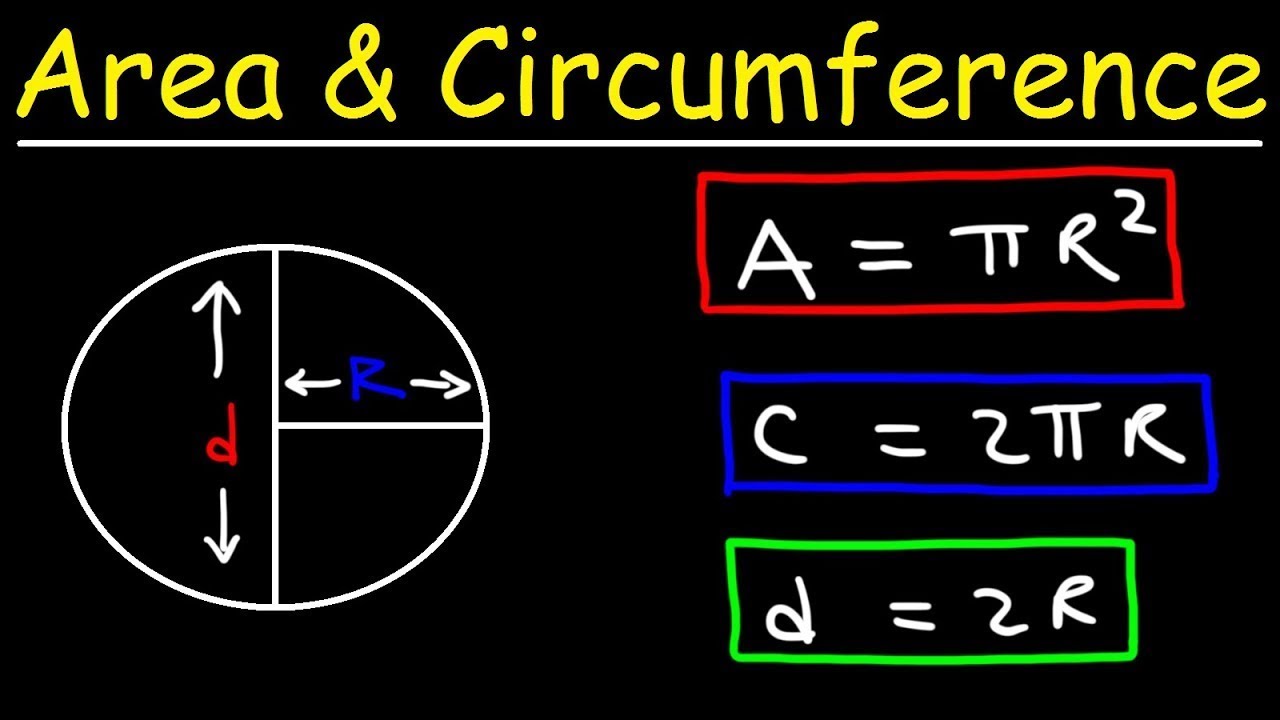
Circles - Area, Circumference, Radius & Diameter Explained!
5.0 / 5 (0 votes)
