GCSE Maths - How to find the Area and Circumference of a Circle (Circles Part 1) #106
Summary
TLDRIn this educational video, viewers learn how to find the circumference and area of a circle by understanding key terms such as circumference, diameter, and radius. The video explains essential formulas, including A = πr² for area and C = 2πr or C = πd for circumference. Two practical examples illustrate the calculations using a radius of 4 cm and a diameter of 10 cm, showcasing the step-by-step process to arrive at the results. The video concludes with a call to action, encouraging viewers to like, subscribe, and visit their website for more resources.
Takeaways
- 😀 The circumference of a circle is the curved line forming its outer boundary.
- 😀 The diameter is a straight line passing through the center of the circle, connecting two points on its boundary.
- 😀 The radius is half the diameter, extending from the center of the circle to the circumference.
- 😀 Circumference is represented by 'C', diameter by 'D', and radius by 'r'.
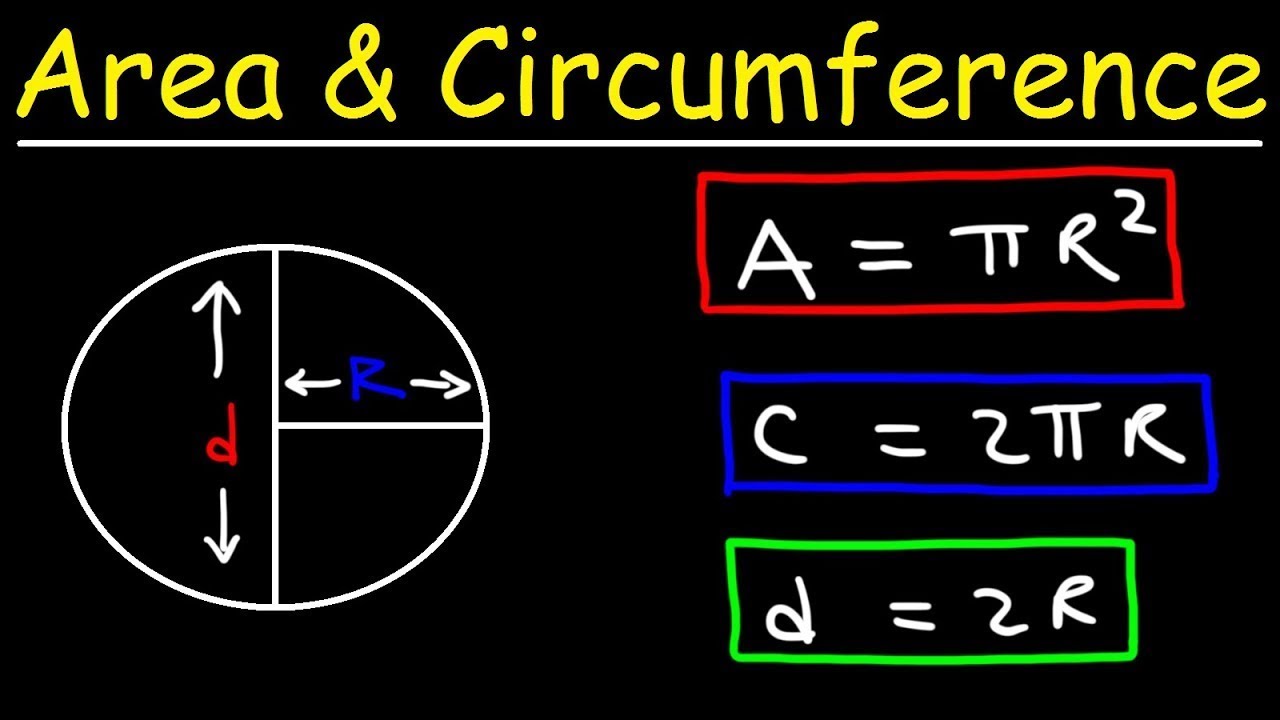
- 😀 The area of a circle is calculated using the formula A = πr².
- 😀 The circumference can be calculated with either C = 2πr or C = πd.
- 😀 Both formulas for circumference are equivalent, as diameter (d) is twice the radius (r).
- 😀 For a circle with a radius of 4 cm, the area is approximately 50.3 cm².
- 😀 The circumference for the same circle is approximately 25.1 cm.
- 😀 If given the diameter of 10 cm, the radius is calculated as 5 cm, leading to an area of 78.5 cm² and a circumference of 31.4 cm.
Q & A
What are the key terms associated with circles discussed in the video?
-The key terms are circumference, diameter, and radius.
How is the circumference of a circle defined?
-The circumference is the curved line that makes up the outside boundary of the circle.
What is the difference between the diameter and the radius?
-The diameter is a straight line that passes through the center of the circle, connecting two points on its boundary, while the radius is a straight line from the center to the circumference, which is half the diameter.
What is the formula for calculating the area of a circle?
-The formula for the area of a circle is A = πr², where r is the radius.
What are the two formulas for calculating the circumference of a circle?
-The two formulas for circumference are C = 2πr (using the radius) and C = πd (using the diameter).
If the radius of a circle is 4 cm, how do you calculate its area?
-To calculate the area, use the formula A = πr². Plugging in the radius: A = π × 4² = π × 16 ≈ 50.3 square centimeters.
How is the circumference calculated if the radius is 4 cm?
-Using the formula C = 2πr, the circumference is C = 2 × π × 4 = 25.1 centimeters.
What is the relationship between diameter and radius?
-The diameter is twice the length of the radius. If you have the radius, you can find the diameter by multiplying by 2.
What area does a circle with a diameter of 10 cm have?
-First, find the radius (which is 5 cm). Then use the formula A = πr²: A = π × 5² = 78.5 square centimeters.
How do you find the circumference of a circle when you know the diameter?
-Using the formula C = πd, for a diameter of 10 cm, the circumference is C = π × 10 = 31.4 centimeters.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Circles - Area, Circumference, Radius & Diameter Explained!

Cara Mencari Keliling dan Luas Lingkaran Jika Jari-jari dan Diameter Diketahui

Cara Menghitung LUAS dan KELILING Lingkaran

How to Calculate Circumference of a Circle (Step by Step) | Circumference Formula
Circumference and area of a circle - exact answers in terms of pi

Radius & diameter from circumference | High School Geometry | High School Math | Khan Academy
5.0 / 5 (0 votes)