Introduction to Limits (NancyPi)
Summary
TLDRIn this video, Nancy introduces the concept of limits in calculus, explaining what a limit is, how to read its notation, and how it appears on a graph. She demonstrates finding limits by approaching a point from the left and right, highlighting that the limit depends on y-values near the point rather than the function's value at that point. The video covers one-sided limits, limits at infinity, and cases where limits do not exist, using clear examples like holes, step functions, and asymptotes. Nancy emphasizes understanding the behavior around a point, providing a foundational guide to limits for beginners.
Takeaways
- 😀 A limit predicts the y-value a function is approaching as x approaches a specific point.
- 😀 The limit notation 'lim x→a f(x) = L' means y-values are approaching L as x approaches a.
- 😀 The answer to a limit is always a y-value, not an x-value.
- 😀 To find a limit, you must check values from both the left (x→a⁻) and right (x→a⁺) sides of the point.
- 😀 If the left-hand limit and right-hand limit are equal, the overall limit exists; if they differ, the limit does not exist (DNE).
- 😀 Holes or undefined points at x = a do not affect the limit; limits depend only on approaching values, not the actual function value at the point.
- 😀 One-sided limits allow you to analyze functions with jumps or discontinuities, using left-sided (x→a⁻) and right-sided (x→a⁺) limits.
- 😀 Limits at infinity examine the behavior of a function as x becomes very large or very negative, often approaching a horizontal asymptote.
- 😀 Even for normal continuous functions, the limit focuses solely on the y-value approached, not necessarily the function’s actual value at that point.
- 😀 The equal sign in limit notation signifies the value the function is approaching, not necessarily the exact value at that x-point.
Q & A
What is a limit in mathematics?
-A limit predicts the y-value that a function is approaching as x gets close to a specific point. It focuses on the behavior around the point, not necessarily the value at the point itself.
How do you read the limit notation \(\lim_{x \to a} f(x)\)?
-It is read as 'the limit of f(x) as x approaches a.' The answer to the limit is always a y-value that the function is approaching as x gets closer to a.
Why do we need limits if we can see the function's value at a point?
-Limits are useful when the function is undefined at a point, has a hole, or behaves differently around that point. They allow us to understand the function's approaching behavior even when the exact value is unclear.
What are left-hand and right-hand limits?
-The left-hand limit is the value y approaches as x comes toward a point from the left side, and the right-hand limit is the value y approaches as x comes toward the point from the right side.
How do you determine the overall limit from a graph?
-You check the left-hand and right-hand limits. If both limits are equal, the overall limit exists and equals that y-value. If they differ, the overall limit does not exist (DNE).
Can the limit exist at a point where the function is undefined?
-Yes. Even if a function has a hole at a point, the limit can exist if the y-values approaching the point from both sides converge to the same number.
What happens to the limit if a function has a defined value at a hole?
-The limit is unaffected by the defined value at the hole. The limit only depends on the values the function approaches around that point, not the function's actual value at the point.
What is a one-sided limit notation?
-A one-sided limit specifies the direction from which x approaches the point. A minus sign (\(x \to a^-\)) indicates approaching from the left, and a plus sign (\(x \to a^+\)) indicates approaching from the right.
How do limits work when x approaches infinity or negative infinity?
-As x approaches infinity or negative infinity, we observe the y-values the function is approaching. The function may approach a horizontal asymptote, giving a limit even though the function never actually reaches infinity.
Why is the equal sign used in limit notation if the function may not equal that value?
-The equal sign in limit notation indicates the y-value the function is approaching. It does not mean the function equals that value at the point, just that it gets arbitrarily close to it.
What is an example of a function where the overall limit does not exist?
-A step function with a jump, where the left-hand limit and right-hand limit at a point are different. For example, if the left limit is 3 and the right limit is 4, the overall limit at that point does not exist (DNE).
Does the limit depend on the function being continuous?
-No. Limits depend on the approaching behavior of y-values, not on the continuity of the function. Even discontinuous functions can have limits at certain points if left and right limits agree.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Limit of a Function using a Graph - Basic/Differential Calculus

04. Limites e Continuidade. | Cálculo I.

Limit Kalkulus Part 4 – Limit Tak Hingga & Asimtot Datar dan Tegak

Limit Kalkulus Part 1: Apa Itu Limit? Penjelasan Mudah & Visual!

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)
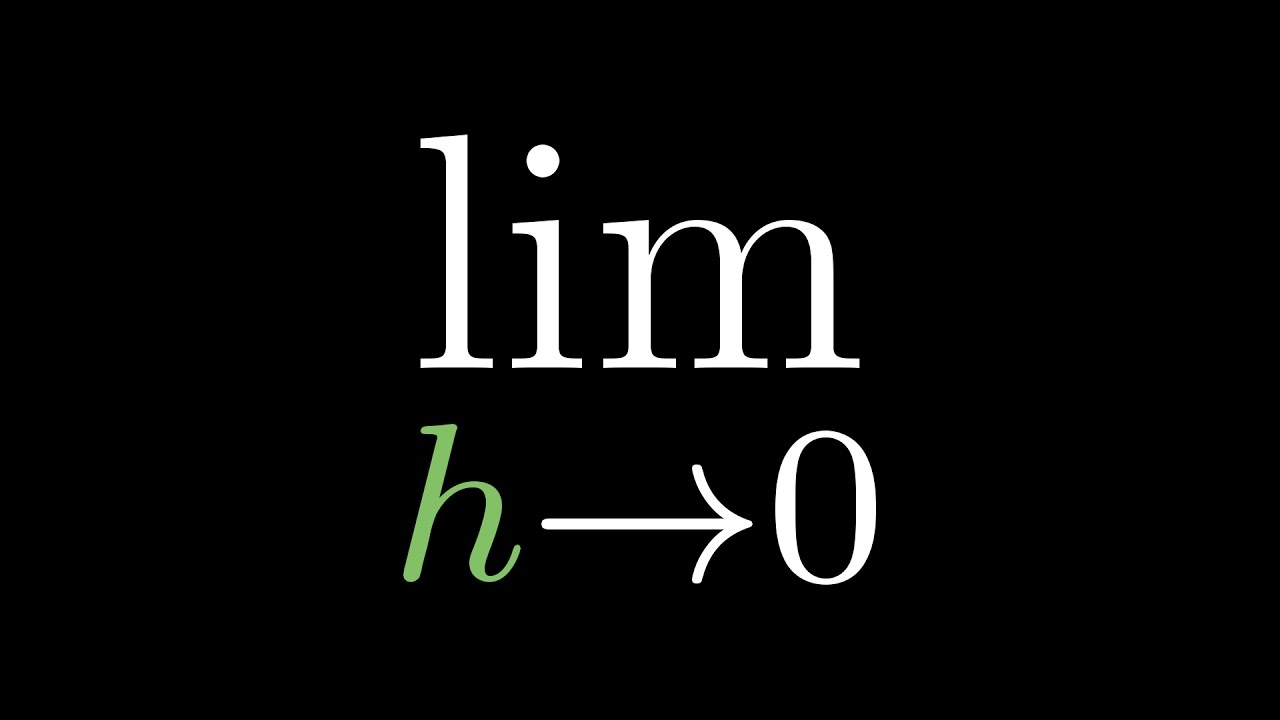
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
5.0 / 5 (0 votes)
