Introduction to Big-O

Summary

In this video, the concept of computational complexity is explored, focusing on Big O notation. It explains how Big O measures the worst-case time and space complexity of algorithms, helping programmers evaluate performance. The video covers different time complexities such as constant, logarithmic, linear, quadratic, and exponential, as well as common algorithm examples like binary search and merge sort. It also discusses why Big O ignores constants and emphasizes the behavior of algorithms as input sizes grow large. Key examples are given to show how these complexities manifest in practical scenarios, helping users understand algorithm efficiency.

Takeaways

• 😀 Big O notation is used to analyze the time and space complexity of algorithms, especially in the worst-case scenario.
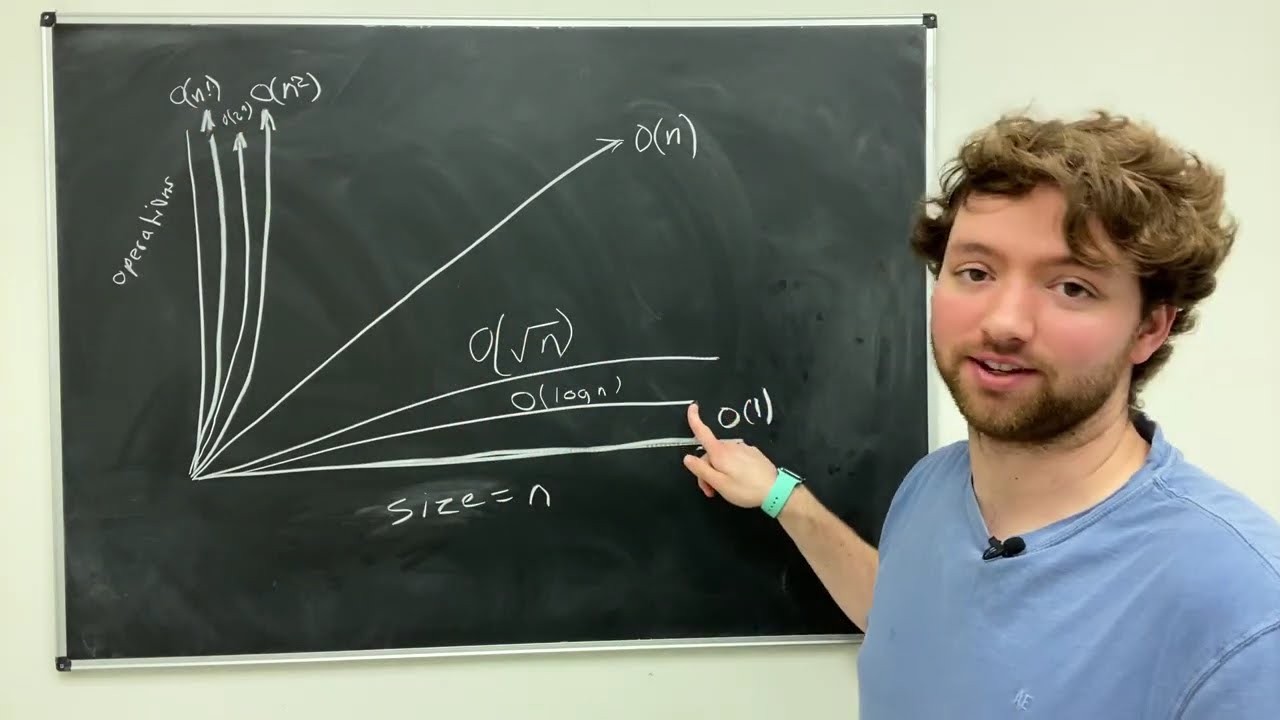
• 😀 Big O only concerns itself with the behavior of an algorithm as the input size grows very large (as n approaches infinity).
• 😀 Constants and multiplicative factors can be ignored in Big O notation, as they do not significantly impact performance for large inputs.
• 😀 When analyzing algorithms, Big O focuses on the largest term (dominant term) in the time or space complexity function.
• 😀 An algorithm with a constant time complexity (O(1)) will always run in the same amount of time regardless of input size.
• 😀 Linear time complexity (O(n)) means the algorithm's running time increases proportionally with the size of the input.
• 😀 Quadratic time complexity (O(n²)) means the algorithm performs an action for each pair of input elements, growing quickly as n increases.
• 😀 Logarithmic time complexity (O(log n)) means the algorithm reduces the problem size by half with each iteration, making it efficient for large inputs.
• 😀 Exponential time complexity (O(2^n)) grows extremely fast as input size increases, often making algorithms with this complexity impractical for large inputs.
• 😀 Binary search is an example of an algorithm with logarithmic time complexity, dividing the input in half each time to efficiently search for an item.
• 😀 Algorithms that involve nested loops or multiple stages can result in higher complexity, such as O(n³), O(n⁴), or even exponential time complexities in extreme cases.

Q & A

What is the main goal when analyzing algorithm performance?

The main goal is to understand how much time and space an algorithm requires to complete its computation. Programmers are primarily concerned with the algorithm’s time complexity and space complexity.

Why is Big O notation used in computational complexity?

Big O notation is used to standardize the way we talk about the time and space complexity of algorithms, focusing on the worst-case scenario. It allows us to describe how algorithms scale with input size.

What does Big O notation focus on when analyzing an algorithm's performance?

Big O notation focuses on the worst-case scenario of an algorithm's performance, specifically how it behaves as the input size grows arbitrarily large.

How does Big O notation relate to the worst-case scenario in sorting algorithms?

In a sorting algorithm, Big O notation refers to the worst-case scenario, which is when the input is arranged in the least favorable way for the algorithm, such as having the largest or smallest number at the end or beginning.

What does the term 'n' typically represent in Big O notation?

In Big O notation, 'n' typically represents the size of the input, such as the number of elements in a list or array.

Why are constants and multiplicative factors ignored in Big O notation?

Constants and multiplicative factors are ignored in Big O notation because they become insignificant as the input size grows infinitely large. The focus is on the scaling behavior of the algorithm.

What is an example of an algorithm with constant time complexity?

An example of an algorithm with constant time complexity (O(1)) is simply accessing an element in an array by its index or performing a basic arithmetic operation, which does not depend on the input size.

What is the time complexity of searching for an element in an unsorted list?

The time complexity of searching for an element in an unsorted list is O(n) because, in the worst case, every element needs to be checked until the target element is found.

How does the binary search algorithm achieve logarithmic time complexity?

The binary search algorithm achieves logarithmic time complexity (O(log n)) by repeatedly dividing the search space in half, discarding one half of the array in each step, thus reducing the problem size exponentially with each iteration.

What is the time complexity of finding all subsets of a set?

The time complexity of finding all subsets of a set is O(2^n) because there are 2^n possible subsets of a set with n elements.