Unit 1 | Lesson 3: The Fibonacci Sequence (Mathematics in the Modern World)
Summary
TLDRIn this lesson, the Fibonacci sequence is introduced through a rabbit reproduction problem. The sequence, discovered by Leonardo Fibonacci, follows a pattern where each term is the sum of the two preceding ones. The lesson explains how Fibonacci applied this pattern to model rabbit populations, leading to the discovery of the Fibonacci numbers. The lesson also explores the Golden Ratio and its presence in nature, such as in sunflower seeds and snail shells. Finally, students are tasked with creating their own Fibonacci spiral artwork to demonstrate their understanding of the sequence and its aesthetic significance.
Takeaways
- 😀 The Fibonacci sequence was introduced by Leonardo of Pisa (Fibonacci), an Italian mathematician.
- 😀 Fibonacci’s real name was Leonardo, and he was also known as 'Leonardo of Pisa' due to his origins.
- 😀 The Fibonacci sequence is tied to a problem involving rabbits, where pairs of rabbits are placed in a pen and reproduce following certain rules.
- 😀 The problem outlined by Fibonacci involves rabbits that produce one male and one female pair every month, starting at one month old.
- 😀 The Fibonacci sequence is generated by adding the two previous terms to get the next one (e.g., 1, 1, 2, 3, 5, 8...).
- 😀 The Golden Ratio, or Fibonacci spiral, is derived from the Fibonacci sequence and can be represented visually through squares and spirals.
- 😀 The Fibonacci spiral is seen in nature, including sunflower seed arrangements, flower petals, and snail shells.
- 😀 The Golden Ratio has a value of approximately 1.618 and is considered a mathematical constant found in various fields like art and architecture.
- 😀 The Fibonacci sequence can be used to predict the growth of rabbit populations, forming a model of exponential growth.
- 😀 The activity encourages students to create original artwork highlighting the Fibonacci spiral, using any medium they are comfortable with.
- 😀 The lesson includes a grading rubric, focusing on accuracy, creativity, visual appeal, and effort, with a total of 100 points.
Q & A
What is the Fibonacci sequence?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It starts with 0 and 1, and the sequence looks like: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.
Why was the Fibonacci sequence separated from other number patterns like arithmetic and geometric sequences?
-The Fibonacci sequence is unique because it grows differently from arithmetic and geometric sequences, where each term is based on a fixed difference or ratio. The Fibonacci sequence adds the two previous numbers to generate the next, which makes it distinct and applicable to various natural phenomena.
Who is Fibonacci and how did he discover the Fibonacci sequence?
-Fibonacci, whose real name was Leonardo of Pisa, was an Italian mathematician. He discovered the Fibonacci sequence through a problem involving rabbits, where he wanted to determine how many pairs of rabbits would exist after one year, based on certain reproductive conditions.
What are the conditions of the Fibonacci rabbit problem?
-The conditions of the Fibonacci rabbit problem are: each pair of rabbits can reproduce once a month, producing exactly one male and one female offspring. Rabbits can only start reproducing when they are one month old.
How many pairs of rabbits did Fibonacci have after one year?
-After one year, Fibonacci had 89 pairs of rabbits, or 178 individual rabbits, based on the reproductive conditions set in the problem.
What is the Golden Ratio and how is it related to the Fibonacci sequence?
-The Golden Ratio is a constant approximately equal to 1.618. It is closely related to the Fibonacci sequence because as the numbers in the sequence increase, the ratio between consecutive numbers approximates the Golden Ratio.
What is the Fibonacci spiral and how is it formed?
-The Fibonacci spiral is formed by drawing squares with side lengths corresponding to the Fibonacci numbers (1x1, 2x2, 3x3, etc.). When these squares are arranged together, a spiral can be drawn within them, which forms a visual representation of the Golden Ratio.
Can you give examples of how the Fibonacci spiral appears in nature?
-The Fibonacci spiral appears in nature in the arrangement of sunflower seeds, the number of petals in flowers, and the shape of snail shells. These patterns follow the proportions defined by the Fibonacci sequence and the Golden Ratio.
What is the objective of the activity given at the end of the lesson?
-The activity's objective is for students to create a drawing that illustrates the Fibonacci spiral. Students are expected to use Oslo paper, emphasize the spiral, and ensure their artwork is original, visually appealing, and neatly done.
What are the grading criteria for the Fibonacci spiral activity?
-The activity is graded based on three criteria: accuracy of the Fibonacci spiral (40%), creativity and visual appeal (40%), and effort and completeness (20%).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

THE FIBONACCI SEQUENCE AND THE GOLDEN RATIO || MATHEMATICS IN THE MODERN WORLD

GEC104 Video Lecture 1 - Mathematics in our World (Part 2): Fibonacci Sequence and Golden Ratio

The Mind-Blowing Mathematics of Sunflowers - Instant Egghead #59

Fibonacci and the Golden Mean
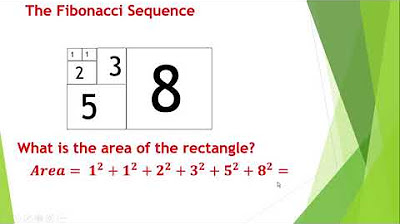
Fibonacci Sequence

EMODULE 1.2 - The Fibonacci Sequence
5.0 / 5 (0 votes)
