Matriks Matematika Wajib Kelas 11 Bagian 3 - Determinan Matriks Ordo 2x2 dan 3x3 dengan cara Sarrus
Summary
TLDRIn this educational video, the host explains how to calculate the determinant of 2x2 and 3x3 matrices. For 2x2 matrices, the process involves multiplying the main diagonal elements and subtracting the product of the side diagonal elements. For 3x3 matrices, the Sarrus method is used to visualize and compute the determinant. The video also covers important matrix properties like the determinant of the transpose, inverse, and scalar multiples of matrices. The host emphasizes the usefulness of these concepts in practical applications like university entrance exams.
Takeaways
- 😀 The determinant of a matrix is only defined for square matrices (matrices with equal numbers of rows and columns).
- 😀 The determinant of a 2x2 matrix can be calculated by multiplying the elements of the main diagonal and subtracting the product of the elements of the other diagonal.
- 😀 For a 3x3 matrix, the determinant can be calculated using the Sarrus method, which involves summing the products of the diagonals and subtracting the products of the side diagonals.
- 😀 A matrix is called singular if its determinant is zero, and non-singular if its determinant is not zero.
- 😀 The determinant of the transpose of a matrix is the same as the determinant of the original matrix.
- 😀 The determinant of the inverse of a matrix is equal to the reciprocal of the determinant of the original matrix.
- 😀 The determinant of the product of two matrices is the product of their determinants.
- 😀 Raising a matrix to a power is equivalent to raising its determinant to the same power.
- 😀 For a matrix multiplied by a constant scalar, the determinant is the constant raised to the power of the matrix's order, multiplied by the determinant of the matrix.
- 😀 Determinants are frequently used in problems related to selection exams, such as PTN or independent selection exams, due to their properties.
- 😀 The video provides a series of practical examples for calculating the determinant of both 2x2 and 3x3 matrices, along with applying determinant properties.
Q & A
What is the determinant of a matrix and how is it written?
-The determinant of a matrix is a scalar value that can be calculated from the elements of a square matrix. It is written as 'det(A)' or sometimes with absolute value signs, such as |A|.
How do you calculate the determinant of a 2x2 matrix?
-To calculate the determinant of a 2x2 matrix with elements 'a', 'b', 'c', and 'd' arranged as follows: [a, b; c, d], the formula is det(A) = ad - bc. This is the product of the main diagonal elements minus the product of the off-diagonal elements.
What is the determinant of a matrix if the matrix is given as [3, 5; 4, 7]?
-For the matrix [3, 5; 4, 7], the determinant is calculated as (3 * 7) - (5 * 4) = 21 - 20 = 1.
How do you calculate the determinant of a 3x3 matrix?
-To calculate the determinant of a 3x3 matrix, we use the Sarrus method. First, write the first two columns of the matrix again next to the original matrix. Then, calculate the sum of the products of the diagonals going from left to right and subtract the sum of the products of the diagonals going from right to left.
What is the determinant of the 3x3 matrix [1, 0, 2; 3, 1, -1; -2, 1, 3]?
-Using the Sarrus method for the matrix [1, 0, 2; 3, 1, -1; -2, 1, 3], the determinant is calculated as (1 * 1 * 3) + (0 * -1 * -2) + (2 * 3 * 1) - (2 * 1 * -2) - (1 * -1 * 3) - (0 * 3 * 1) = 3 + 0 + 6 - (-4) - (-3) - 0 = 3 + 0 + 6 + 4 + 3 = 16.
What is a singular matrix?
-A singular matrix is a square matrix whose determinant is zero. This means it does not have an inverse.
What is a non-singular matrix?
-A non-singular matrix is a square matrix whose determinant is not zero. Such a matrix has an inverse.
What is the property of the determinant of the transpose of a matrix?
-The determinant of the transpose of a matrix is the same as the determinant of the original matrix. In other words, det(A^T) = det(A).
How do you calculate the determinant of the inverse of a matrix?
-The determinant of the inverse of a matrix is the reciprocal of the determinant of the original matrix. That is, det(A^(-1)) = 1 / det(A).
What is the relationship between the determinant of the product of two matrices and the individual determinants?
-The determinant of the product of two matrices is equal to the product of their individual determinants. That is, det(A * B) = det(A) * det(B).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
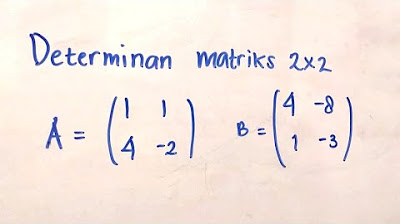
Menentukan Determinan Matriks ordo 2x2 | Matematika SMA

Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial

Cara Menentukan Determinan dan Invers Matriks

Matriks Matematika Wajib Kelas 11 - Invers Matriks Ordo 2x2 dan Ordo 3x3 dan Sifat-sifatnya

MATRIKS RUANG VEKTOR | MENCARI DETERMINAN DENGAN METODE OBE

Inverse Matrices and Their Properties
5.0 / 5 (0 votes)
