Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
Summary
TLDRThis video tutorial explains how to find the determinant of both 2x2 and 3x3 matrices. The instructor starts by covering the basics of calculating the determinant for a 2x2 matrix, providing examples for practice. Next, the video moves on to the more complex 3x3 matrix, breaking it down step by step into smaller 2x2 matrices and demonstrating the calculation process through multiple examples. The video ends by encouraging viewers to explore more mathematical content on the creator's channel for further learning.
Takeaways
- 🔢 The video focuses on finding the determinant of both 2x2 and 3x3 matrices.
- ➗ For a 2x2 matrix, the determinant is calculated using the formula: determinant = (a * d) - (b * c).
- 🧮 Example 1 for a 2x2 matrix: With values [3, 5, -4, 7], the determinant is calculated as 41.
- 📝 A second example for a 2x2 matrix is provided, with values [-7, 4, 8, -3], resulting in a determinant of 1.
- 🔍 For a 3x3 matrix, you break it down into 2x2 matrices using cofactor expansion along the first row.
- ➖ The formula for a 3x3 matrix involves alternating signs and removing rows and columns to find the 2x2 matrices.
- 📊 Example 1 for a 3x3 matrix: With values [2, 4, -3, 5, 7, 6, 8, 1, 9], the determinant is calculated as -441.
- 🔢 Another example for a 3x3 matrix: With values [5, 7, 8, 4, -3, 6, 1, 7, 9], the determinant is calculated as -29.
- 📈 The video provides step-by-step breakdowns of how to simplify and evaluate the matrices.
- 📚 The video ends by encouraging viewers to explore more topics such as algebra, chemistry, and physics by visiting the speaker’s channel and playlists.
Q & A
What is the basic formula for finding the determinant of a 2x2 matrix?
-The determinant of a 2x2 matrix is calculated as: det(A) = a * d - b * c, where the matrix is represented as [[a, b], [c, d]].
How do you find the determinant of the matrix [[3, 5], [-4, 7]]?
-Using the formula det(A) = a * d - b * c, for the matrix [[3, 5], [-4, 7]], the determinant is 3 * 7 - 5 * -4 = 21 + 20 = 41.
What steps should you take to find the determinant of a 3x3 matrix?
-To find the determinant of a 3x3 matrix, reduce the matrix into smaller 2x2 matrices by eliminating the first row and alternating columns, then apply the 2x2 matrix determinant formula and combine the results.
How do you simplify a 3x3 matrix into three 2x2 matrices?
-For each element in the first row, eliminate its corresponding row and column, then form a 2x2 matrix with the remaining elements. Repeat this for each element in the first row.
What is the determinant of the matrix [[-7, 8], [4, -3]]?
-The determinant of the matrix [[-7, 8], [4, -3]] is calculated as: -7 * -3 - 8 * 4 = 21 - 32 = -11.
What is cofactor expansion in the context of finding the determinant of a 3x3 matrix?
-Cofactor expansion refers to the process of expanding the determinant of a 3x3 matrix by breaking it down into 2x2 matrices and applying alternating signs to the elements of the first row.
How would you evaluate the determinant of the 3x3 matrix [[2, 4, -3], [5, 7, 6], [8, 1, 9]]?
-First, form three 2x2 matrices by eliminating rows and columns: det(A) = 2 * det([[7, 1], [6, 9]]) - 4 * det([[5, 1], [6, 9]]) + (-3) * det([[5, 7], [8, 1]]). Then calculate each determinant and combine.
What is the significance of alternating signs when calculating a 3x3 determinant?
-The alternating signs ensure that the cofactor expansion accounts for the orientation of each 2x2 submatrix in the original 3x3 matrix.
How do you approach finding the determinant of a matrix like [[5, 7, 8], [4, -3, 6], [1, 7, 9]]?
-Start by applying cofactor expansion along the first row: det(A) = 5 * det([[-3, 6], [7, 9]]) - 7 * det([[4, 6], [1, 9]]) + 8 * det([[4, -3], [1, 7]]), and then solve each 2x2 matrix.
What is the final determinant of the 3x3 matrix [[5, 7, 8], [4, -3, 6], [1, 7, 9]]?
-After calculating the 2x2 determinants and combining them with the appropriate signs, the determinant of the matrix is -29.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Matriks Matematika Wajib Kelas 11 Bagian 3 - Determinan Matriks Ordo 2x2 dan 3x3 dengan cara Sarrus

Matriks Matematika Wajib Kelas 11 - Invers Matriks Ordo 2x2 dan Ordo 3x3 dan Sifat-sifatnya

Cara Menentukan Determinan dan Invers Matriks

MATRIKS RUANG VEKTOR | MENCARI DETERMINAN DENGAN METODE OBE
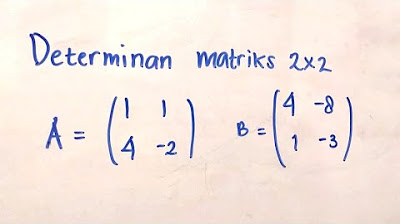
Menentukan Determinan Matriks ordo 2x2 | Matematika SMA

Inverse Matrices and Their Properties
5.0 / 5 (0 votes)