INTRODUCTION OF HYPERBOLA || PRE-CALCULUS 2
Summary
TLDRThis video provides an introduction to hyperbolas, explaining their standard equations and properties. It covers the forms of hyperbolas with horizontal and vertical transverse axes, with specific focus on the center, vertices, and foci. The lesson also delves into the concept of the conjugate axis and how to calculate key elements like the distance between the center and the foci. Additionally, the video discusses the graphing of hyperbolas, the fundamental rectangle, and the asymptotes, offering a visual guide for understanding their structure and behavior. It's an essential lesson for grasping the foundational elements of hyperbolas.
Takeaways
- 😀 The standard form of the hyperbola equation is x²/a² - y²/b² = 1, where the transverse axis is horizontal.
- 😀 When the transverse axis is vertical, the equation of the hyperbola changes to y²/a² - x²/b² = 1.
- 😀 The general equation of a hyperbola can also be written as (x - h)²/a² - (y - k)²/b² = 1 for horizontal transverse axis and (y - k)²/a² - (x - h)²/b² = 1 for vertical transverse axis.
- 😀 A hyperbola is defined by two fixed points called the foci, and the difference between the distances from any point on the hyperbola to the foci is constant.
- 😀 Unlike an ellipse, the sum of distances in a hyperbola is not constant; rather, the difference is.
- 😀 The hyperbola consists of two branches, which can open either horizontally (right or left) or vertically (up or down).
- 😀 The center of the hyperbola is the midpoint between the two vertices, which are located at the intersection of the transverse axis and the curve.
- 😀 The conjugate axis is perpendicular to the transverse axis and plays a role in defining the shape and orientation of the hyperbola.
- 😀 In a hyperbola with the equation x²/a² - y²/b² = 1, the distance from the center to the foci is given by c = √(a² + b²).
- 😀 The asymptotes of the hyperbola are the diagonals of the fundamental rectangle, and their equations are y = ±(b/a) * x.
- 😀 The lattice rectum, which helps define the curvature of the hyperbola, is determined by the formula b²/a for horizontal orientation and vice versa for vertical orientation.
Q & A
What is the standard equation of a hyperbola in its horizontal transverse axis form?
-The standard equation of a hyperbola in its horizontal transverse axis form is: x²/a² - y²/b² = 1.
What is the standard equation of a hyperbola in its vertical transverse axis form?
-The standard equation of a hyperbola in its vertical transverse axis form is: y²/a² - x²/b² = 1.
How does the transverse axis orientation affect the standard equation of a hyperbola?
-When the transverse axis is horizontal, the standard equation takes the form x²/a² - y²/b² = 1. When the transverse axis is vertical, the equation becomes y²/a² - x²/b² = 1.
What does the center of a hyperbola represent in its graph?
-The center of a hyperbola is the midpoint of the line segment joining its two vertices and is a key reference point for the graph.
How do the foci of a hyperbola differ from those of an ellipse?
-For a hyperbola, the constant relates to the difference between the distances from any point on the hyperbola to the two foci, whereas for an ellipse, the constant is the sum of these distances.
What are the branches of a hyperbola, and how do they open?
-A hyperbola has two branches, which can open either horizontally (right/left) or vertically (up/down), depending on the orientation of the transverse axis.
What is the meaning of the conjugate axis in a hyperbola?
-The conjugate axis is perpendicular to the transverse axis and helps define the rectangle that is fundamental to the graph of a hyperbola.
What is the formula to calculate the distance from the center to the foci of a hyperbola?
-The distance from the center to the foci of a hyperbola is calculated as c = √(a² + b²), where 'a' is the distance from the center to the vertex and 'b' relates to the conjugate axis.
What is the significance of the vertices in the graph of a hyperbola?
-The vertices of a hyperbola are the points where the hyperbola intersects the transverse axis, and they are crucial for determining the shape and orientation of the hyperbola.
How do the asymptotes of a hyperbola relate to its graph?
-The asymptotes of a hyperbola are straight lines that intersect at the center of the hyperbola, and their equations are given by y = ±(b/a)x, defining the boundary behavior of the hyperbola as it extends to infinity.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
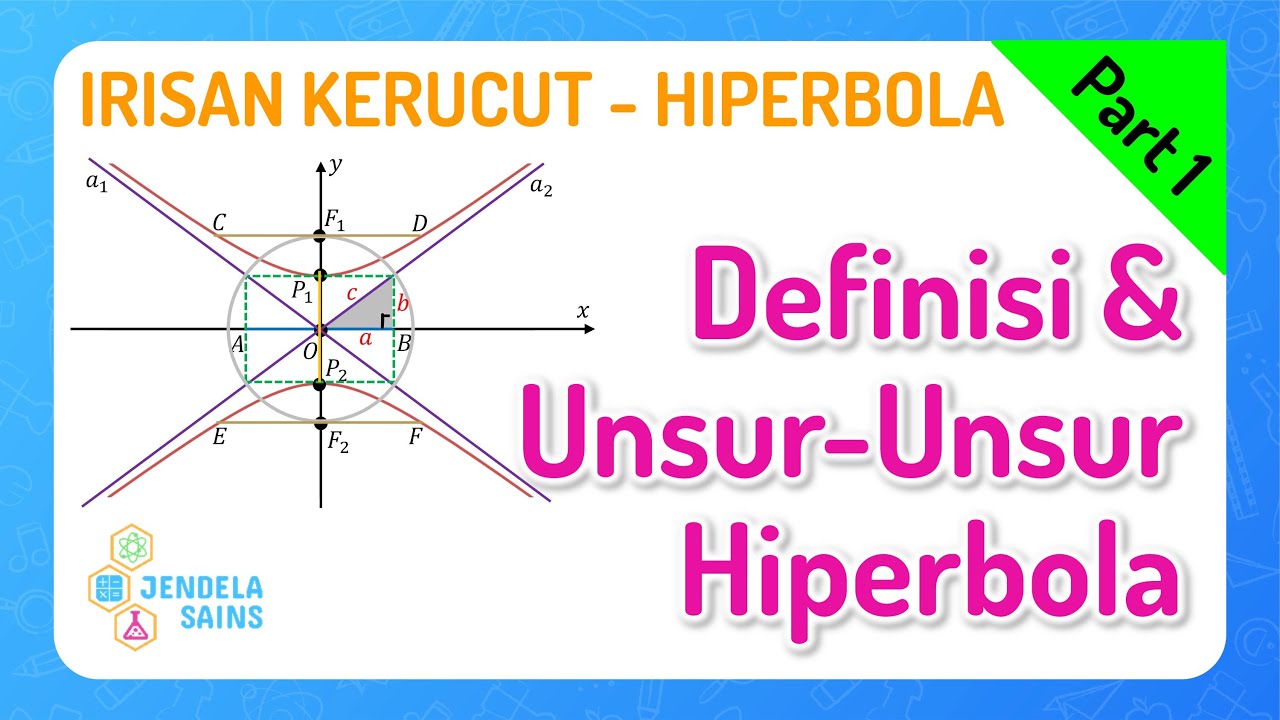
Irisan Kerucut - Hiperbola • Part 1: Definisi dan Unsur-Unsur Hiperbola

Conic Sections (Parabola, Ellipse & Hyperbola) All Important Formulas & Tricks for JEE Mains 2023

Conic sections: Intro to hyperbolas | Conic sections | Algebra II | Khan Academy

Illustrating Linear Equations in Two Vairables | Writing Linear Equations in Standard Form
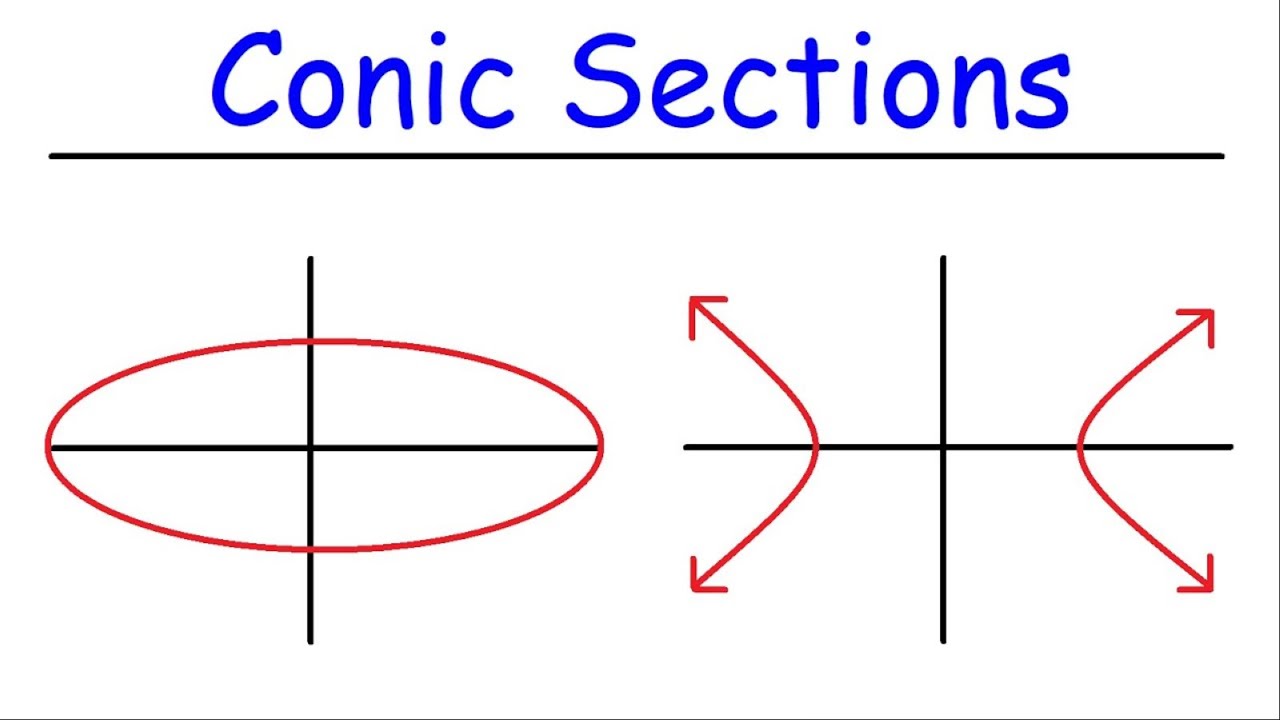
Conic Sections - Circles, Semicircles, Ellipses, Hyperbolas, and Parabolas

What are Conic Sections? | Don't Memorise
5.0 / 5 (0 votes)
