Conic sections: Intro to hyperbolas | Conic sections | Algebra II | Khan Academy

Summary

In this video, the speaker demystifies hyperbolas, contrasting them with other conic sections like circles and ellipses. He emphasizes the importance of understanding their equations and characteristics rather than relying solely on memorization. The speaker presents the standard forms of hyperbolas, explains how to derive their asymptotes, and discusses the direction in which they open. With visual illustrations, he clarifies that hyperbolas approach their asymptotes without touching them, providing an engaging and intuitive explanation of these mathematical concepts. Future videos promise to include numerical examples for further understanding.

Takeaways

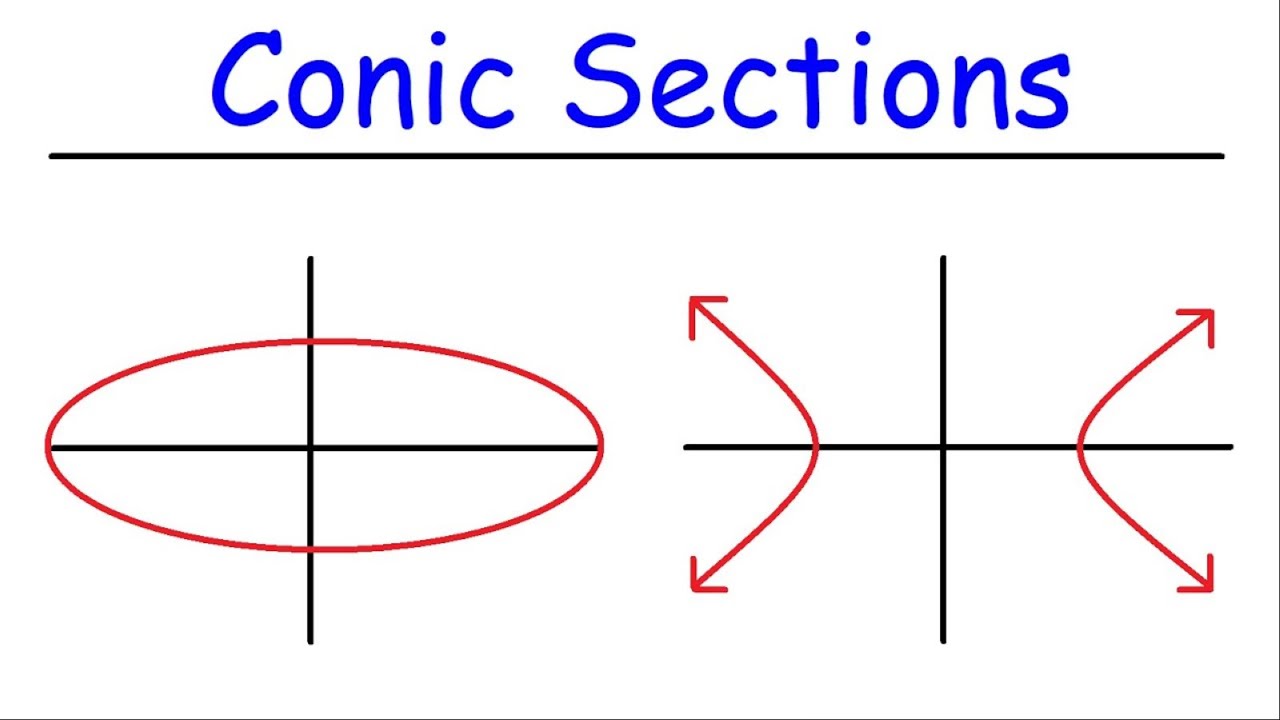
• 😀 Hyperbolas can be more confusing than other conic sections, such as circles and ellipses, due to their complex algebraic representations.
• 🌀 The standard equations for hyperbolas are different based on their orientation: horizontal hyperbolas have 'x' first, while vertical hyperbolas have 'y' first.
• 📏 Asymptotes are important lines that hyperbolas approach but never touch; they help define the shape of the graph.
• 🔍 To graph hyperbolas, it's crucial to determine if they open horizontally or vertically, based on their equation.
• 📊 The equations can be manipulated to express 'y' in terms of 'x' to find asymptotes and better understand the graph's behavior.
• 🚀 As 'x' approaches infinity, the behavior of the hyperbola approximates the asymptotes, which can be expressed mathematically.
• 👨‍🏫 It’s essential to re-derive formulas rather than just memorize them to avoid confusion during tests or practical applications.
• 💡 When graphing a hyperbola, start by plotting its asymptotes, which guide the placement of the hyperbola’s branches.
• 🔄 If 'y' can equal zero, the hyperbola opens left and right; if 'x' can equal zero, it opens up and down.
• 🔗 Understanding hyperbolas has real-world applications, including modeling phenomena in physics and telecommunications.

Q & A

What is the primary focus of the video?

The video focuses on understanding hyperbolas as one of the conic sections, comparing it to circles, ellipses, and parabolas.

How is the equation of a hyperbola different from that of a circle and an ellipse?

The hyperbola's equation includes a minus sign between the two squared terms, unlike the circle and ellipse which use a plus sign. Specifically, a hyperbola can be expressed as x²/a² - y²/b² = 1 or y²/b² - x²/a² = 1.

Why does the speaker prefer to derive the asymptotes rather than memorize formulas?

The speaker believes that memorizing formulas can lead to confusion and forgetting them over time. Instead, deriving the asymptotes helps reinforce understanding of their relationship to the hyperbola.

What are the asymptotes of a hyperbola, and how are they determined?

The asymptotes are lines that the hyperbola approaches but never touches. They are determined by the equations y = ±(b/a)x, derived from analyzing the behavior of the hyperbola as x approaches positive or negative infinity.

What indicates whether a hyperbola opens horizontally or vertically?

If the x² term is positive in the standard form of the hyperbola (x²/a² - y²/b² = 1), it opens horizontally. Conversely, if the y² term is positive (y²/b² - x²/a² = 1), it opens vertically.

What happens to the value of y as x approaches infinity for a hyperbola?

As x approaches infinity, y approximates ±(b/a)x, indicating that y becomes increasingly large and follows the slope of the asymptotes.

Can a hyperbola cross the y-axis, and what does that imply?

For the horizontal hyperbola (x²/a² - y²/b² = 1), it cannot cross the y-axis since y=0 leads to a contradiction. However, for the vertical hyperbola (y²/b² - x²/a² = 1), it can cross the y-axis.

How does the speaker plan to address potential confusion with hyperbolas?

The speaker plans to clarify concepts by providing practical examples and drawing hyperbolas, ellipses, and circles with actual numbers in future videos.

What is the significance of the terms 'a' and 'b' in the hyperbola's equation?

'a' represents the distance from the center to the vertices along the transverse axis, while 'b' represents the distance from the center to the vertices along the conjugate axis, impacting the shape and orientation of the hyperbola.

What educational approach does the speaker advocate for learning hyperbolas?

The speaker advocates for a conceptual understanding through derivation and visualization rather than rote memorization of formulas, emphasizing a deeper comprehension of the material.