Decision Tree using C4.5 Algorithm Solved Numerical Example | C4.5 Solved Example by Mahesh Huddar
Summary
TLDRThis video explains how to build a decision tree using the C4.5 algorithm, with a step-by-step approach. The presenter uses a dataset containing attributes like CGPA, interactiveness, practical knowledge, and communication skills, with a target class of job offers (yes/no). The video covers the calculation of essential metrics such as entropy, information gain, split info, and gain ratio for each attribute. It demonstrates the process of selecting the best attribute, starting with CGPA as the root node, and constructing the decision tree. The final decision tree is used to predict job offers based on the given attributes.
Takeaways
- 😀 The C4.5 decision tree learning algorithm is used to build a decision tree with a simple example.
- 😀 The dataset consists of four attributes: CGPA, interactiveness, practical knowledge, and communication skills, with the target class being whether a job offer is extended (Yes/No).
- 😀 The first step in building the decision tree is selecting the root node, which involves calculating the gain ratio for each attribute.
- 😀 The gain ratio is calculated by considering metrics like entropy, information gain, and split information.
- 😀 The entropy of the target class (job offer) is calculated using probabilities of 'Yes' and 'No' examples in the dataset.
- 😀 After calculating the entropy of the whole dataset, the next step is to calculate the entropy for each attribute to measure the effectiveness of each attribute in making decisions.
- 😀 The attribute with the highest gain ratio is chosen as the root node, and in this example, CGPA was selected due to its highest gain ratio.
- 😀 After selecting CGPA as the root, further branching is done by evaluating the possible values of CGPA (greater than or equal to 9, greater than or equal to 8, less than 8).
- 😀 At each level, further splits are made by calculating the gain ratio for the remaining attributes, such as interactiveness, practical knowledge, and communication skills.
- 😀 The decision tree is built recursively until a leaf node is reached where the data no longer requires further splitting, resulting in 'Yes' or 'No' as the final labels.
- 😀 The final decision tree provides a model for predicting job offers based on the values of the attributes, following the C4.5 decision tree learning algorithm.
Q & A
What is the purpose of the C4.5 algorithm in decision tree learning?
-The C4.5 algorithm is used to build a decision tree by selecting the most informative attributes at each node based on the concept of Information Gain and Gain Ratio, aiming to predict the target class (e.g., Job Offer in this case).
How do you calculate the entropy of a dataset in the C4.5 algorithm?
-The entropy is calculated using the formula: Entropy(S) = - Σ P(Ei) * log2(P(Ei)), where P(Ei) is the probability of each class (e.g., 'Yes' or 'No') in the dataset.
What does the term 'Gain Ratio' refer to in the C4.5 algorithm?
-The Gain Ratio is a metric used to select the most informative attribute by dividing the Information Gain of an attribute by its Split Information, helping to prevent overfitting by considering both the attribute's ability to classify and the diversity of the attribute's values.
Why is CGPA chosen as the root node in the decision tree?
-CGPA is chosen as the root node because it has the highest Gain Ratio compared to the other attributes (Interactiveness, Practical Knowledge, and Communication Skills), making it the most informative for splitting the dataset.
How is the Information Gain of an attribute calculated in the C4.5 algorithm?
-Information Gain is calculated by subtracting the entropy of the attribute from the entropy of the entire dataset: Information Gain = Entropy(Whole Dataset) - Entropy(Attribute).
What role does 'Split Info' play in the calculation of Gain Ratio?
-Split Info measures the intrinsic information of an attribute based on its possible values, helping to prevent attributes with many distinct values from dominating the decision tree. It is used in the denominator of the Gain Ratio formula.
What happens if an attribute’s value leads to all examples being of the same class in C4.5?
-If an attribute’s value leads to all examples being of the same class (e.g., all 'Yes' or all 'No'), the decision tree terminates at that point, and the class is assigned as the leaf node without further splitting.
Why are some branches of the decision tree not expanded further in the C4.5 algorithm?
-Some branches are not expanded further if they already lead to pure subsets (where all examples belong to the same class), meaning no further attribute-based splitting is needed.
How does the decision tree handle situations where multiple attributes have the same Gain Ratio?
-When multiple attributes have the same Gain Ratio, the C4.5 algorithm selects one of them arbitrarily, or based on a predefined order, to continue the tree-building process.
What is the final step after building the decision tree using C4.5?
-After building the decision tree, the final step is to use the tree to classify new examples based on the decisions made at each node, ultimately assigning a class (e.g., 'Yes' or 'No' for Job Offer).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Building Decision Tree Models using RapidMiner Studio
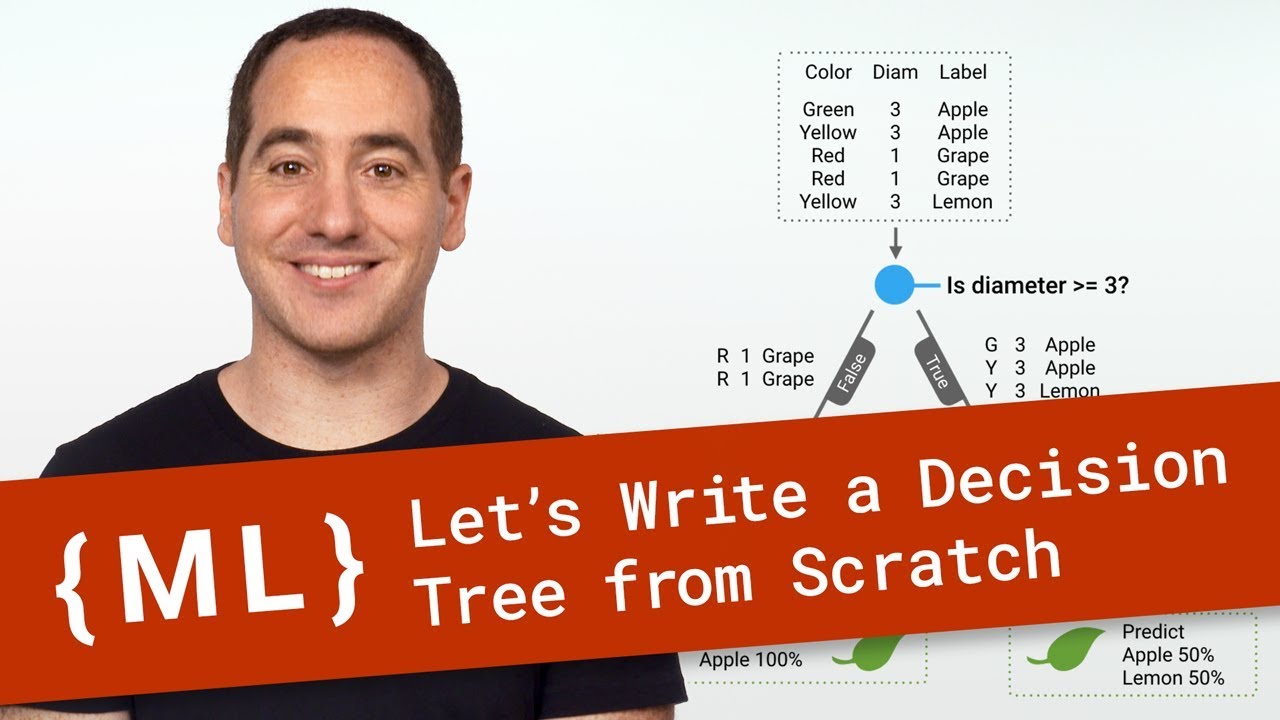
Let’s Write a Decision Tree Classifier from Scratch - Machine Learning Recipes #8

Decision Tree Solved | Id3 Algorithm (concept and numerical) | Machine Learning (2019)

Decision Tree Pruning explained (Pre-Pruning and Post-Pruning)

Learning Decision Tree
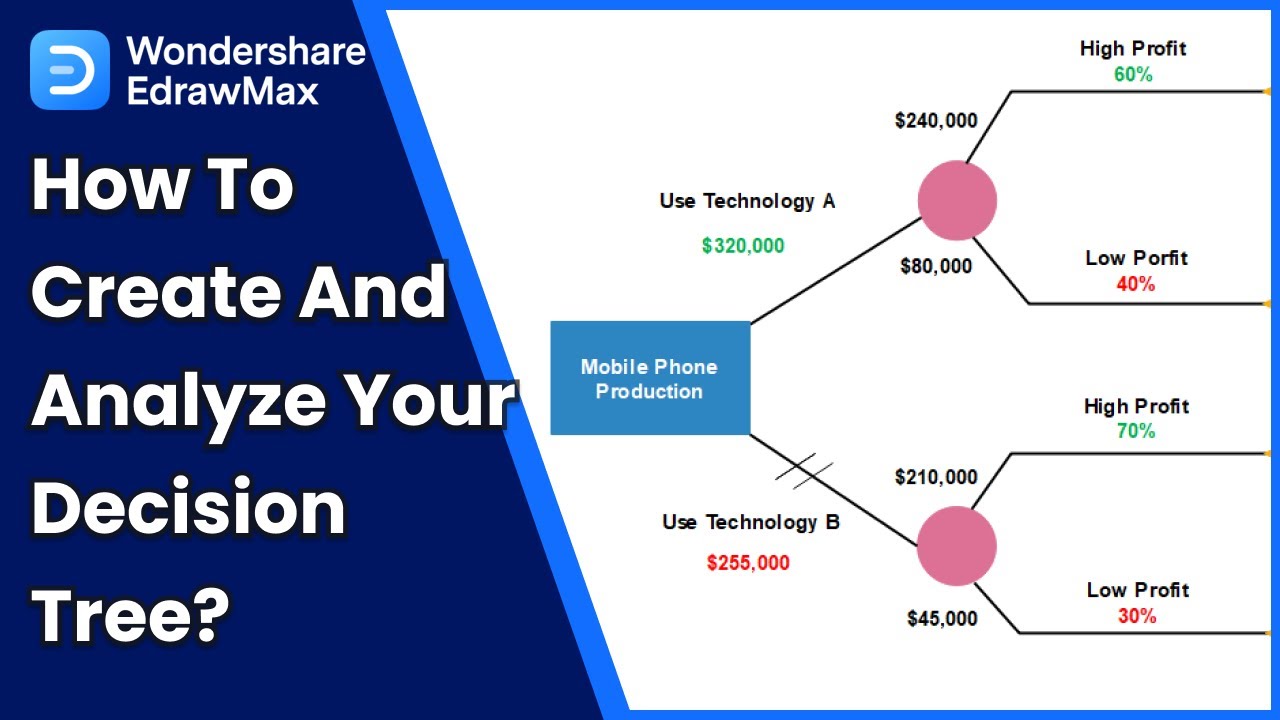
How to Create a Decision Tree | Decision Making Process Analysis
5.0 / 5 (0 votes)
