OPERASI VEKTOR | Penjumlahan, Pengurangan, dan Perkalian Vektor | Matematika Lanjut FASE F
Summary
TLDRIn this video, the topic of vector operations, specifically vector addition, subtraction, and multiplication, is explored for 10th-grade students in the MIPA program. The explanation covers both geometric and algebraic methods for these operations, with visual illustrations and step-by-step breakdowns of the calculations. Using examples like the movement of objects between different points (A to B to C), the video demonstrates how vectors can be combined or modified through simple mathematical principles. The video also includes practice problems to further solidify the concepts.
Takeaways
- 😀 Vectors are geometric quantities that have both magnitude and direction, and their operations like addition, subtraction, and multiplication are essential in mathematics.
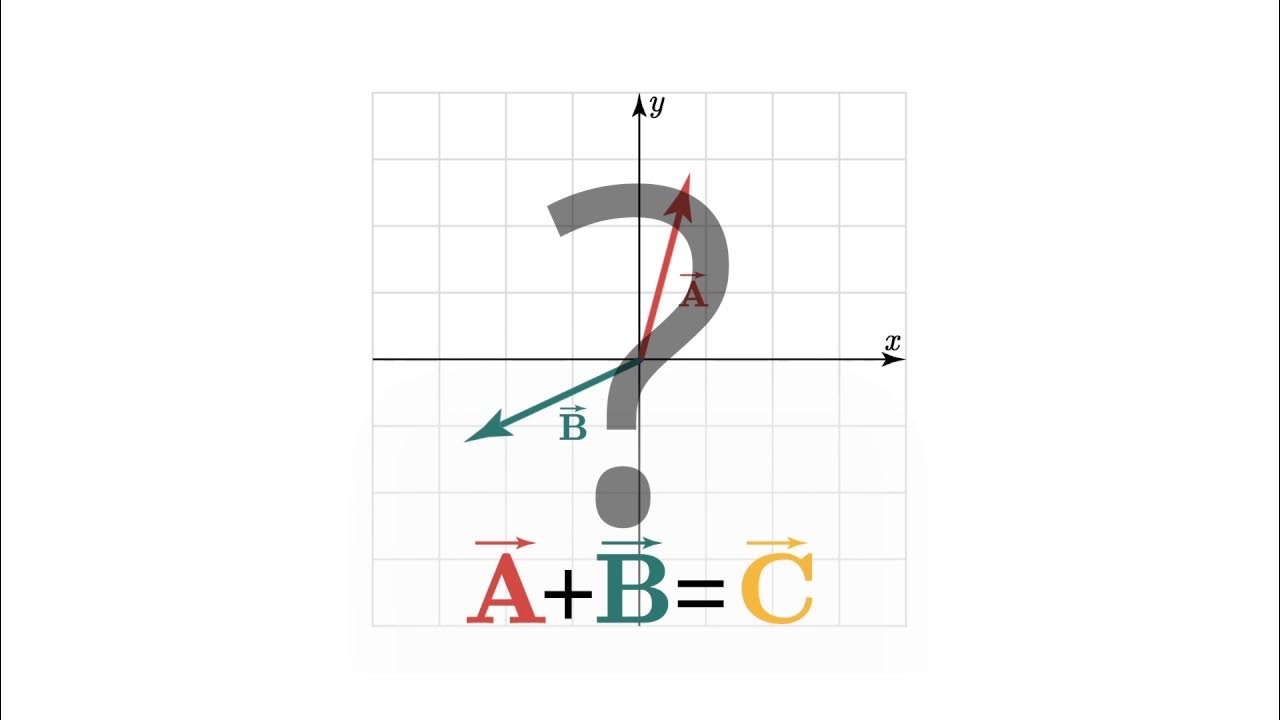
- 😀 Vector addition can be represented geometrically by connecting the tail of one vector to the head of another, forming a resultant vector.
- 😀 The commutative property holds for vector addition, meaning that vector A + vector B is the same as vector B + vector A.
- 😀 Vector subtraction is represented geometrically by reversing the direction of the second vector and then performing the addition.
- 😀 Unlike vector addition, vector subtraction is not commutative, meaning that vector A - vector B is not the same as vector B - vector A.
- 😀 Scalar multiplication of vectors changes the magnitude of the vector, but the direction depends on whether the scalar is positive or negative.
- 😀 Multiplying a vector by a positive scalar preserves its direction, while multiplying by a negative scalar reverses the direction.
- 😀 Analytically, vector addition and subtraction involve the addition or subtraction of their corresponding components (i.e., x, y, and z coordinates).
- 😀 In scalar multiplication, each component of the vector is multiplied by the scalar value.
- 😀 To solve vector problems, understanding both geometric and algebraic representations is crucial for applying vector operations correctly.
- 😀 Example problems help reinforce concepts, such as calculating the resultant vector of a parallelogram or finding values from specific vector equations.
Q & A
What is the main focus of the video?
-The video focuses on vector operations in mathematics, specifically vector addition, subtraction, and multiplication. It is aimed at students in class 10 MIPA.
How is vector addition explained geometrically in the video?
-Vector addition is explained geometrically by using the example of a ball moving from point A to point B and then from point B to point C. The resulting vector from A to C can be represented as the sum of the vectors AB and BC.
What is the key takeaway about the commutative property of vector addition?
-The video explains that vector addition is commutative, meaning that the order of addition does not affect the result. This is demonstrated by showing that vector U + vector V is the same as vector V + vector U.
What does the video say about vector subtraction geometrically?
-In vector subtraction, the direction of the vector being subtracted is reversed. The example uses vectors U and V, and the subtraction of vector V from vector U is illustrated by reversing the direction of vector V and then combining it with vector U.
How is vector multiplication by a scalar described in the video?
-Scalar multiplication is explained by showing that multiplying a vector by a scalar results in stretching or shrinking the vector. If the scalar is positive, the direction remains the same; if the scalar is negative, the direction is reversed.
Can you explain the algebraic method for vector addition mentioned in the video?
-In the algebraic method, if two vectors U and V are represented by their components (e.g., U = (a, b, c) and V = (d, e, f)), vector addition is done by adding the corresponding components: U + V = (a + d, b + e, c + f).
What is the difference between vector U - V and vector V - U, according to the video?
-Vector U - V is the result of subtracting vector V from vector U, while vector V - U is the opposite, with the directions reversed. The video emphasizes that vector subtraction is not commutative, meaning U - V is not equal to V - U.
What is the geometric representation of multiplying a vector by 2, as shown in the video?
-When a vector is multiplied by 2, it is effectively duplicated in the same direction. The video uses the example of vector 2U, where the vector U is drawn twice to show the effect of scalar multiplication.
What does the video say about the properties of a parallelogram in relation to vectors?
-In the context of a parallelogram, the video explains that the vector PQ (denoted as U) and vector PS (denoted as V) form a parallelogram. The diagonal from point O to point S represents the resultant vector, which is the sum of vectors U and V.
How is the question about determining vector SQ explained geometrically?
-To find vector SQ, the video suggests adding vectors SP and PQ. This is because the path from S to Q can be traversed by first moving along vector SP and then along vector PQ.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

03 02 Fisika Dasar 1- Operasi Vektor

Operasi Vektor Secara Analitik dan Geometri (Vektor Bagian 3) Matematika Peminatan Kelas 10

Vektor Matematika Kelas 10 : Konsep Dasar Vektor Matematika Peminatan Kelas 10 - Part 1

Vektor pada dimensi tiga | Vektor dimensi 3

Grandezas vetoriais x escalares - VETORES - Aula 1 - Prof. Marcelo Boaro
0.2 Vector Operators
5.0 / 5 (0 votes)
