03 02 Fisika Dasar 1- Operasi Vektor

Summary

This video script delves into vector operations, focusing on vector addition through graphical and analytical methods. It explains how to graphically add vectors by drawing and aligning their representations, emphasizing precision in depiction. The script also covers vector subtraction and the concept of scalar multiplication. Analytically, it introduces vector addition by components and the importance of direction in vector operations. Further, the script explores vector multiplication, including scalar-vector multiplication and the two types of vector-vector multiplication: dot product, resulting in a scalar, and cross-product, yielding another vector. The tutorial is designed to aid understanding in kinematics and dynamics, using clear examples and step-by-step explanations.

Takeaways

• 😀 The video script is a tutorial on vector operations, focusing on vector addition and multiplication.
• 📏 Two methods for vector addition are discussed: graphical and analytical, with an emphasis on precision in graphical representation.
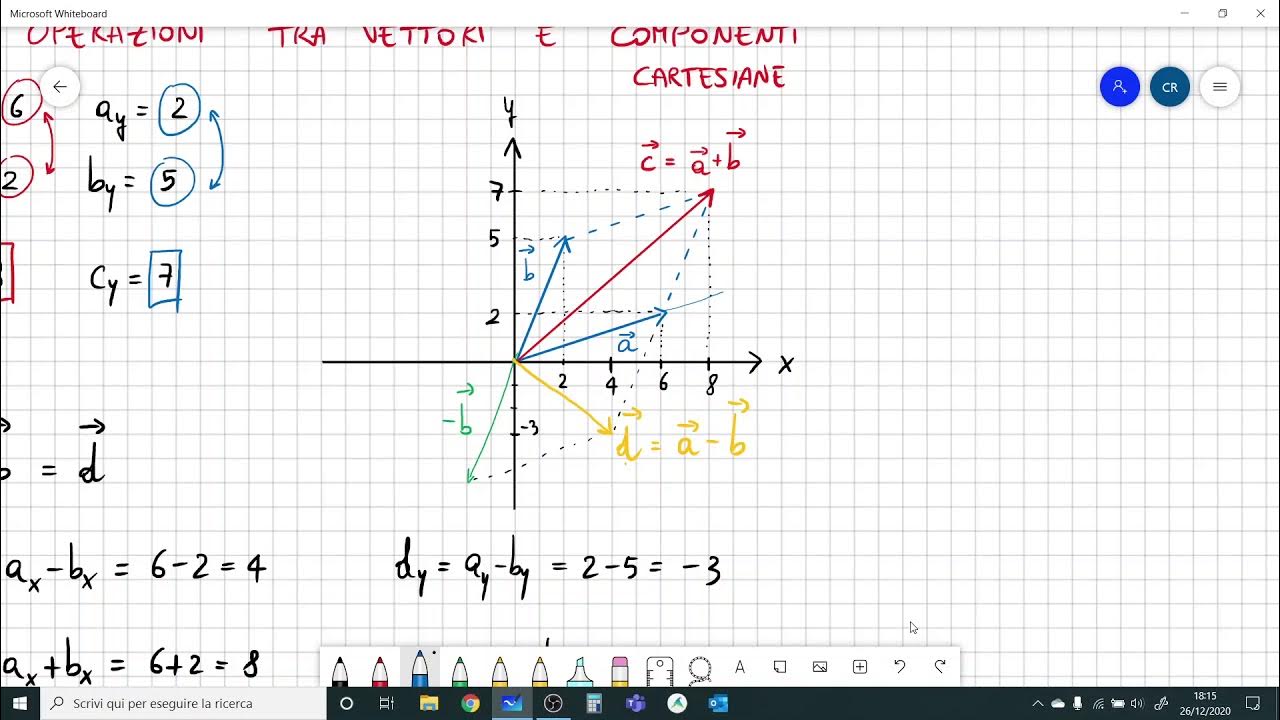
• 🖼️ The graphical method involves drawing vectors accurately according to their magnitude and direction without any analytical calculations.
• ✏️ Analytical addition of vectors requires understanding the components of vectors and performing calculations based on their projections onto the coordinate axes.
• 🔄 The script explains that vector addition is commutative, meaning the order of addition does not change the result.
• ➖ Subtraction of vectors is covered, illustrating that subtracting a vector is equivalent to adding its negative.
• 🔢 The tutorial highlights the importance of performing vector operations only on vectors with the same direction and clarifies common mistakes in vector addition.
• 📐 The script introduces vector multiplication, including scalar multiplication and the two types of vector-vector multiplication: dot product and cross product.
• 📉 For scalar multiplication, the tutorial shows how a vector is scaled by a constant factor, which can be positive, negative, or zero.
• 📌 The dot product is explained as a scalar result of the multiplication of two vectors, calculated as the product of their magnitudes and the cosine of the angle between them.
• 📚 The cross product is introduced as a vector result of the multiplication of two vectors, associated with rotation and the right-hand rule in three-dimensional space.

Q & A

What are the two methods discussed for vector addition?

The two methods discussed for vector addition are the graphical method and the analytical method.

What tools are required for the graphical method of vector addition?

For the graphical method of vector addition, tools such as a ruler, protractor, and graph paper are required.

How is the resultant vector found using the graphical method?

In the graphical method, the resultant vector is found by drawing vector B and then from the tip of vector B, drawing vector C. The resultant vector is then drawn from the initial point of vector B to the tip of vector C.

What property of vector addition is demonstrated when adding vector B and vector C in a specific order?

The property of commutativity is demonstrated when adding vector B and vector C, as the order in which they are added does not change the resultant vector.

How is the subtraction of vectors represented graphically?

The subtraction of vectors is represented graphically by reversing the direction of the vector being subtracted. For example, to subtract vector C from B, you would reverse the direction of vector C and add it to vector B.

What is the significance of the dot product in vector operations?

The dot product is significant in vector operations as it results in a scalar value, representing the product of the magnitudes of the vectors and the cosine of the angle between them.

What is the physical interpretation of the cross product in three-dimensional space?

The cross product in three-dimensional space is related to rotational systems or rotations and is often associated with the right-hand rule, which is used to determine the direction of the resulting vector.

How are the components of the cross product calculated in Cartesian coordinates?

In Cartesian coordinates, the components of the cross product are calculated using the determinant of a matrix formed by the unit vectors i, j, and k, and the corresponding components of the vectors being multiplied.

What is the result of the dot product when two vectors are orthogonal?

When two vectors are orthogonal (perpendicular), the result of the dot product is zero because the cosine of the angle between them is zero.

Why is it important to consider the direction of the vectors when performing vector operations?

The direction of the vectors is important in vector operations because it affects the outcome of operations like addition, subtraction, and the cross product, which depend on the relative orientation of the vectors.

Outlines

00:00

📐 Introduction to Vector Operations

This paragraph introduces the concept of vector operations, specifically focusing on vector addition. Two methods are mentioned for understanding vector addition: graphical and analytical. The graphical method involves precise drawing without any analytical calculations, requiring tools like a ruler and protractor. The analytical method is not described in detail in this paragraph but is implied to involve calculations. The paragraph emphasizes the importance of precision in drawing vectors for the graphical method and sets the stage for further exploration of vector operations.

05:02

🔍 Graphical Method for Vector Addition

The second paragraph delves into the graphical method of vector addition. It explains that this method involves drawing vectors accurately according to their magnitude and direction. The process involves drawing one vector, then starting from the tip of its arrow, drawing another vector to represent the addition. The resultant vector is drawn from the tail of the first vector to the tip of the second. The paragraph also discusses the commutative property of vector addition, where the order of addition does not change the result. It also touches on the concept of subtracting vectors graphically by reversing the direction of the vector being subtracted.

10:03

📐 Analytical Vector Addition and Scalar Multiplication

The third paragraph transitions into the analytical approach for vector addition and introduces scalar multiplication. It explains that analytical addition of vectors requires considering the components of vectors along the x and y axes. The paragraph provides an example of adding vectors A and B by projecting their components onto the x and y axes and then summing these components. The concept of scalar multiplication is also introduced, where a vector is multiplied by a scalar, resulting in a new vector. The paragraph emphasizes the rules for vector operations and the importance of understanding these for further studies in kinematics and dynamics.

15:05

🔢 Scalar Multiplication and Dot Product

This paragraph focuses on scalar multiplication and the dot product of vectors. It provides an example of scalar multiplication where a vector is multiplied by a constant, resulting in a new vector. The dot product is introduced as a multiplication operation between two vectors that results in a scalar. The paragraph explains that the dot product involves projecting one vector onto another and then multiplying this projection by the magnitude of the other vector. The properties of the dot product in a Cartesian coordinate system are discussed, including the orthogonality of the axes and the resulting products when vectors are perpendicular.

20:08

✖️ Cross Product and Its Applications

The fifth paragraph introduces the cross product, a vector multiplication operation that results in a vector perpendicular to the plane containing the two original vectors. It explains the geometric interpretation of the cross product and its relation to the right-hand rule. The paragraph provides examples of how to calculate the cross product in three-dimensional space and discusses the implications of the cross product in physics, such as its use in describing rotational movements and the concept of torque. The right-hand rule is emphasized as a method to determine the direction of the resulting vector from the cross product.

25:10

🚀 Summary of Vector Operations

The final paragraph summarizes the vector operations covered in the script, including graphical and analytical methods for vector addition, scalar multiplication, dot product, and cross product. It highlights the importance of understanding these operations for various applications in physics and engineering. The paragraph concludes by setting the stage for further learning in subsequent videos, promising more in-depth exploration of these concepts.

Keywords

💡Vector

A vector is a quantity that has both magnitude and direction. In the context of the video, vectors are fundamental as they are used to illustrate various operations such as addition, subtraction, and scalar multiplication. The script mentions vector addition graphically, where vectors are represented by arrows, and their addition is performed by placing the tail of one vector to the head of another.

💡Vector Addition

Vector addition is the process of combining two or more vectors to produce a resultant vector. The video explains two methods for vector addition: graphical and analytical. Graphically, it's done by 'head-to-tail' method, where one vector is drawn from the tip of the previous vector, as demonstrated with vectors B and C. Analytically, it involves breaking down vectors into their components and adding them together.

💡Scalar Multiplication

Scalar multiplication is the operation of multiplying a vector by a scalar, which is a numerical value that can change the magnitude of the vector but not its direction. The script provides an example of this with a vector A being multiplied by a scalar C, resulting in a new vector with the same direction but a magnitude scaled by C.

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two vectors and returns a scalar. It is defined as the product of the magnitudes of the two vectors and the cosine of the angle between them. The script explains that in a Cartesian coordinate system, the dot product can be calculated using the formula a.b = a_x * b_x + a_y * b_y + a_z * b_z, where a_x, a_y, a_z and b_x, b_y, b_z are the components of vectors a and b respectively.

💡Cross Product

The cross product is an operation on two vectors in three-dimensional space that results in a third vector which is perpendicular to the plane containing the two input vectors. The script mentions that the cross product is related to rotation and is consistent with the right-hand rule, which is used to determine the direction of the resulting vector.

💡Graphical Method

The graphical method is a technique used to solve mathematical problems by visually representing them. In the video, the graphical method is used to explain vector addition by drawing vectors as arrows on a coordinate system and then adding them by placing one vector's tail at the head of the other.

💡Analytical Method

The analytical method involves solving mathematical problems using formulas and calculations rather than graphical representations. The script contrasts this with the graphical method, showing how vectors can be broken down into their x, y, and z components and then added together using algebraic operations.

💡Commutative Property

The commutative property states that the order in which two operations are performed does not change the result. The video script mentions this property in the context of vector addition, noting that the order in which vectors are added does not affect the outcome, i.e., vector B + vector C is the same as vector C + vector B.

💡Orthogonal

Orthogonality in geometry means that two lines or vectors are perpendicular to each other. The script refers to the orthogonality of the x, y, and z axes in a Cartesian coordinate system, which is crucial for understanding how the dot product and cross product are calculated in three-dimensional space.

💡Right-Hand Rule

The right-hand rule is a common mnemonic for determining the orientation of a vector that is perpendicular to two other vectors. The script explains the cross product in the context of the right-hand rule, stating that if you align your fingers of your right hand in the direction of the first vector and curl them towards the second vector, your thumb will point in the direction of the cross product.

Highlights

Introduction to vector operations, focusing on vector addition.

Two methods for vector addition: graphical and analytical approaches.

Graphical method requires precision in drawing vectors without analytical calculations.

Tools needed for graphical vector addition include a ruler and protractor.

Procedure for graphical vector addition by drawing vectors and their sum.

Commutative property of vector addition is demonstrated.

Subtraction of vectors is analogous to adding a vector with the opposite direction.

Explanation of scalar multiplication with vectors.

Graphical representation of vector subtraction and scalar multiplication.

Analytical method for vector addition requires considering the direction of vectors.

Example of incorrect vector addition due to ignoring vector directions.

Correct approach to analytical vector addition with components in the same direction.

Introduction to vector multiplication, including scalar-vector and vector-vector products.

Scalar multiplication of a vector results in a new vector.

Dot product (scalar product) between two vectors results in a scalar.

Procedure for calculating the dot product using the angle between vectors.

Cross product (vector product) between two vectors results in another vector.

Cross product is related to rotation and the right-hand rule in three-dimensional space.

Calculating the cross product using components and the right-hand rule.

Summary of vector operations covered: addition, scalar multiplication, dot product, and cross product.

Anticipatory guidance for the next video part focusing on further vector operations.

Transcripts

Ayo kita kembali ke 1000 ya dari segala

sesuatu dengan topi Factor kali ini kita

masuk pada bagian kedua videonya yaitu

mengenai operasi vektor Oke sekarang

kita akan mempelajari mengenai operasi

vektor utama dari penjumlahan vektor nah

terjemahan factory ini nanti ada dua

metode yang bisa kita lakukan adalah

metode grafis dan analisis kita mulai

dari metode grafis m ini adalah sesuai

namanya grafis artinya sini kita hanya

menggambarkan tidak ada sedikitpun

perhitungan secara analitik yang akan

dilakukan jadi modalnya adalah

menggambar tentunya menggambarnya harus

presisi hatinya nanti kalau menggambar

vektor ini harus digambar sesuai dengan

ketentuannya ya minimal jika anda

mengerjakan vektor secara grafis Maka

Anda membutuhkan

Pa alat tulis ya alat bantu misalkan

penggaris dan busur derajat dan baiknya

dalam sebuah kertas milimeter blok Oke

kita coba saja di sini ya ini adalah

vektor B yang berwarna kuning dengan

besaran arah ketika gambar dan vektor C

berwarna biru dengan arah dan besar

seperti pada gambar sudah mulai ingin

menghitung berapa vektor b + c Seperti

apa Factor hasil akhirnya nanti akhirnya

adalah dalam bentuk panah juga di sini

ya the mulai b + c berarti kita model

vektor B Gambarkan ulang persis seperti

apa Contohkan disini Jika Anda coba

adalah tool ini berapa panjangnya berapa

sudutnya Anda replika ini ya membuat

replikanya berikutnya adalah ditambah C

maka Gambarkan vektor C dari mana

mulainya Mulailah dari ujung panah

Factor sebelumnya batik

Herbert tadi disini ujungnya kita

lanjutkan dengan vektor C

Hai Nah sudah kalian beetambah C berarti

Brahmana hasilnya hasilnya adalah Anda

tarik Garis dari titik pangkal Factor

awal ke titik ujung vektor akhirnya

seperti ini ini adalah vektor b + c

sebutan yang tidak penamaannya Oke

sekarang investor-state tambah b dengan

cara yang sama kita ke Jakarta pilihan

urutan ya cek dulu baru b maka mulailah

vektor C lanjutkan dengan vektor B dan

kita tarik Garis dari pangkal awal ke

ujung akhir itulah vektor C tambah b

Jika dilihat vektor b + c dengan vektor

set + B di sini memiliki panjang yang

sama dan arah juga yang sama artinya Apa

artinya adalah dan sifat komutatif

disini yaitu vektor B + vektor c itu

sama saja dengan cb34b artinya adalah

I am posisinya anda ubah-ubah tidak

mengubah bentuk akhirnya

Hai Nah sekarang bagaimana kalau di

kurang ya kalau dikurang semuanya telah

penjumlahan juga

di sini ya sekarang misalkan pengennya B

dikurang Ice

Ayo kita pahami dulu hal

Oh berarti kalau B digoreng isi

sebenarnya sama saja dengan b ditambah

minus C ya sama tematik ini berlakukan

karena plus kali min nanti Mimin juga

akhirnya jadi saya bertahan pada konsep

penjumlahan di sini ya oke batik B

ditambah minus C red-orange sudah punya

tapi saya enggak punya VLC berapa Nah

kalau saya punya vektor C seinto Victor

Bu minus c-nya caranya bagaimana tinggal

balikkan arah panahnya saja

Hai nanti kita lihat ini ya Konsep ini

ada di perkalian skalar dengan vektor

jadi kalau saya punya vektor c c ingin

punya Factor negatif c-nya Ya udah

berarti tinggal arah panahnya dibalik

saja nanti beta + C kita Gambarkan benya

Gambarkan ditambah minuse batik gambar

kan minus c dan hasil akhirnya seperti

Hai sekarang bagaimana kalau C minus B

berarti itu adalah C ditambah minus

di Desa Butuh kemana mis Band Seperti

apa vektornya tinggal balikan aja arah

panahnya ke dapat Factor minus B batik C

ditambah minus B kita kerjakan metodenya

yang biru peetamina cd-nya yang berwarna

orange berarti vektor C minus B itu yang

seperti ini sekarang kita lihat

dikurangi C dengan C kurangin D

panjangnya sama cuman panahnya kok

berlawanan Oh berarti simpulkan bahwa B

minus itu = negatif dari ceines Drift

oke Ini adalah cara menjumlahkan vektor

secara grafis jadi tidak ada perhitungan

analitik sedikitpun yang anda lakukan

full menggambar di sini tapi syaratnya

adalah harus presisi

Hai hey sekarang bagaimana kalau semen

menghitung vektor penjumlahannya secara

analitis Nah ada sebuah hal yang penting

untuk Diingat dan diikuti yaitu

penjumlahan itu hanya dapat dilakukan

pada vektor yang memiliki arah yang sama

hatinya kalau saya punya Factor satu

arahnya misalkan ke X1 arahnya kepiye

nanti Anggaplah itu dua makhluk yang

berbeda nggak bisa dijumlahkan oleh anda

yah

Hai ini contohnya ya

Oke siap punya vektor v = 2 I + vektor W

= 7 C Tentukan V tambah

Hai ini sangat mudah jika kita memegang

prinsip atas ini namun kenyataannya

seringkali menjumpai jawaban-jawaban

seperti ini berapakah V tambah W

vektornya = 92 plus 709 kehilangan aja

arahnya atau seperti ini 9 hitam +

Hai Kak ini mah sama-sama angka jumlah

in cuman Islam ajinya enggak boleh di

sebelah in kayak gini atau kayak gini

lagi yang lebih sering Oke lagi ya

hantam aja dua Ita maju jaya 9ij ini

semua jawaban salah kenapa vc nya sia

terjemah lakukan pada Ferrari yang

memiliki arah yang sama biar vektor v

arahnya yg ke sumbu X Metal W arahnya J

ke sumbu y Anggaplah mohawke hewan ini

ya Ini adalah kuda inilah gajah

G2 gajah Taqwa 7 Buddha yang bukan2 gak

kuda atau dua gajah laku 7 kuda tapi kan

tetep aja dua gajah ditambah 7 budaya

seni ayat2 gajah ditambah 7 udah berarti

kalau ada v = 2 x + 7 j&w nya tapi

hasilnya adalah jangan dilupakan karena

dia berbeda arahnya ya tetep pos

dipisahkan dengan tanda tambah Ini oke

Ya jadi contohnya misalkan ini saya

punya velg ditambah 5j minus 6 k dan

vektor H = 2 imej tambah 4K itu kan

g-plus Ha dan coba tuliskan Disini

Hai ye tambah h ini ringtonenya ini

Factor ha iya saya coba bedakan warnanya

ya untuk yang arahnya X atau arahnya yg

warna merah arah J atau arah y warna

biru dan arah Z atau k warnet hijau maka

menjumlahkannya Bagaimana bisa

dijumlahkan kalau akhir sama berarti

Yati hanya bisa dengan i-j dengan Je

kakak maka dipisahkan dengan ih saja

yo yah jadi kalau ada yg bahas hanyalah

satu ini disitu ya mesti paham Iya jadi

jangan bingung kalau ioc berapa angkanya

berarti

Hai berikutnya adalah yang joknya

j5 j&t minus 3j dan yang hanya minus 6

dan + 4 ya nanti satui tambah2 I

hasilnya adalah tiga i5j minus 3j

hasilnya adalah 2 j6 kata Mbah 4K

hasilnya adalah minus 2 kah maka Ini

hasilnya Jangan naze32 dua jangan sampai

3 plus 2 minus 233 ijc jangan ya Tapi

tetap begini karena lihat ya i-j-k dada

arah Harus Terpisah

The Key seperti itu cara menjumlahkan

vektor si analitis dalam bentuk vektor

satuan seperti ini ya

Hai bagaimana kalau yang ingin

dijumlahkan dalam bentuk panah tapi

ingin analitik itu yang kita bahas

berikutnya Hei sekarang kita masih ingin

menjumlahkan vektor secara analitis

namun sekarang berbeda dengan sebelumnya

ya tadi sebelumnya kita menunjukkan

Factor yang bentuknya itu dalam vektor

satuan dijkt setelah Bagaimana kalau

Factor ingin dijumlahkan itu bentuknya

dalam anak panas seperti ini

oh ya bisa kan saya punya Factor A8

besarnya a kecil dan arahnya gelas sudut

Alfa terhadap sumbu x positif bidang

datar dan ada vektor B yang berwarna

biru ini besar vektornya b kecil dan

arahnya adalah sudut beta terhadap sumbu

x negatif atau bidang datar

Hai nah sini menjumlahkan ini tanpa apa

gambar jadinya analitis ya maka caranya

adalah yang tadi kita telah pelajari di

video sebelumya itu Kita sesuaikan dulu

per komponennya jadi nanti jumlahnya itu

adalah istilahnya resultan vektor nya

jadi kalau aku tambah b berarti hasilnya

adalah resultan vektor a dan b senam

akan saja Factor er vektor resultan ya

oke maka caranya adalah kita harus

proyeksikan semua sudut semua Factor di

sini ya ini vektor a b c terhadap sumbu

x

Hai jadi hadaa pada arah X dan proyeksi

vektor a pada sumbu y a y kemudian by

juga sama vektor b proyeksinya dalam

sumbu-x bsdan dalam sumbu-y by apa nih

tanda pas negatifnya tak sini ya karena

proyeksi vektor a dalam arah X dia

berada disisi sumbu x positif maka X

nilainya positif

KYT ini ada di sumbu y positif kan ya

atau arahnya ke arah yang positif Mbak

sih positif sementara yang vektor B kita

disini proyeksi di sumbu x ya dia ada di

sumbu x negatif atau dia ke arah kiri

batu dia negatif ini pun sama iyanya ke

bawah ke sumbu y negatif mati dia

negatif hutan yang lainnya ya ya

Hai Ginanti ini akan berpengaruh

Hai Rati tinggal jumlahkan er adalah a

tambah b itu adalah ada aksi tambah aj6

c-nya adalah BSI + by Terjemahkan ingat

ini tadi aturannya hanya dilakukan pada

vektor yang terakhir sama berarti X

dengan x y dengan yeya ini dengan yang

ini aye dengan Bridge seperti ini ya

berarti er dalam arah X resultan dalam

arah x adalah a x + b x kita ingat ya

ekskul ini akan

Hai tadi batik Acos sudutnya a cos Alfa

ditambah yang BX berapa B cos beta ini

Kenapa negatif karena yang BX arahnya ke

kiri lihat ini ya merah kanan biru kiri

saling melawan kan mengurangi yang

sesungguhnya sama saja tadi kan kalau

komponen dia berarti shines Karya Bhakti

ini A3 Salva positif ya ditambah best

Chinese beta tapi negatif

Hai tinggal masukkan angkanya Maka nanti

hasil akhirnya dapat install sebagai

berikut jadi nanti saya telah vektor

resultan = sekon dalam arah XV tambah

resultan dalam arah

Hai seperti itu ya Ini adalah bagaimana

kita menjumlahkan vektor secara analitis

TNI nanti adalah konsep yang akan sangat

sering kita gunakan di materi materi

kinematika dinamika dan lain-lain

Hai hey berikutnya adalah sakitkah

memahami mengenai penjumlahan maka

operasi berikutnya adalah perkalian nah

perkalian vektor ini ada dua jenis nya

itu Perkalian antara vektor dengan

skalar dan Perkalian antara aktor dengan

vektor untuk perkalian vektor dengan

skalar nanti hasilnya adalah Factor kita

lihat contohnya ya sementara pekan

vektor-vektor ada dua jenis lagi yaitu

perkalian titik alias dot product yang

hasilnya nanti adalah skalar dan

perkalian silang atau cross-product yang

hasil nanti adalah Factor kita bahas

satu persatu perkalian ke kalian ini Nah

untuk perkalian vektor dengan skalar

sini contohnya adalah misalkan ada

vektor A dan itu axc Plus

JJ tambah Hz tak ingin dikalikan dengan

suatu konstanta salah satunya akan

kepada arahnya C c-nya bilangan riil di

boleh positif boleh negatif boleh

pecahan boleh bilangan bulat muat 03

silakan

Hai Nah maka Gimana hasilnya seperti ini

ya Jadi kalau ada konsultansi dikalikan

a.bac ABC dikalikan dengan ini semua IC

tambah y + z kaya mana 13 dibutuhkan

saja ya Bakti C kali aksi tambah C

kalian yay tambah cek Aliya Z k501uq

hasilnya gimana hasilnya Ya sudah hijrah

inilah hilangkan Maka hasilnya Factor

masih ada ijtihadnya contohnya Ini

misalkan ya P = 2 x + 10 j-min 6k

hitunglah minus setengah kali

Hai speknya Factor minus tengahnya

adalah skala rekan konstanta skalar ini

kalikan jadi mudah seperti ini kan ya

minus Tengah Kali P = berarti minus

Tengah Kali 2i plus-minus Tengah Kali

10j plus-minus setengah kali min 6 Kak

Mbaknya pertama ini sekali 2 = min 1 Min

setengah kali 10 Min 5 misalnya 6 adalah

+ 3 Ini hasilnya BNI mi5 J + 3K inikan

Factor hasilnya

halo ah sesuaikan ya di mudahkan ya Nah

tadi contohnya ada vektor B

Hai berapa vitamin osb masa-masa dengan

the TV terbaik kali karmina sabtu nanti

hasilnya Factor juga tapi negatifnya

seperti itulah ya Eh salah kita beralih

pada operasi perkalian titik yah jadi

disini kita sudah mempelajari mengenai

perkalian antara vektor dengan skalar

sekarang Factor yaitu untuk jenis

perkalian titik alias dot product ya

simbol titik tersebut adalah ini titik

ini ya Nah jadi misalkan Saya punya

vektor a besarnya biru dan vektor B

berwarna kuning kemudian sudut yang

diapit oleh kedua faktor ini adalah

theta nilai

Hai Kakak jika sein mengawetkan serat

titik arah vektor a dengan b jadi a.de

itu kira-kira seperti ini ilustrasinya

ya jadi makna dari perkalian titik ini

adalah salah satu faktornya kita

proyeksikan terhadap vektor lainnya

contohnya adalah B ini Saya prediksikan

ke vektor A dan vektor a batik anite

tanya kesini proyeksi berarti adalah B

cos Teta dikalikan hasil proyeksi ini

dikalikan dengan besar vektor satunya

lagi itu adalah perkalian titik jadi

a.by hasilnya adalah a besarnya vektor a

di kalikan komponen vektor B pada peta

ah jadi abco Seta

Di mana kau yang dimasukkannya foto aja

sama saja sinilah Abby posted aja di

Kodam V Tentukan vektor p.v. Turki abad

type C cos Teta pi ini besarnya ya di

sini terlihat ya ini besar abis AB

coaster tak Hati Disini sudah tidak ada

lagi vektornya hasilnya adalah skalar

nanti hasilnya Hanya berupa angka tidak

ada lagi yg jdi situ

Hai nah

Hai dengan koordinat yang kita miliki

itu cartesian kita punya sebuah sifat

yang khas yaitu ketiga sumbu x y z ini

dia saling orthogonal atau saling tegak

lurus 90° antara masing-masing jadi

antara X dengan y tegak lurus antara X

dengan Z2 kurus antara j&t Tegal Rusia

Ketika anda melihat sudut dari sebuah

ruangan ke atas ke samping dan ke arah

Anda yah Nah di sini karena dia sendiri

kurus

Hai sudutnya sebelah jahat maka nilai

cos nya kan sama dengan nol nol itu ya

artinya apa kalau saya mengalihkan

serat.id antara arah X dengan arah y

Berarti antara I dengan J berapa

hasilnya batik klo sekali Katie dengan

j-batik kan nanti ini besar Nyai kali

besarnya J kembar nya Sabtu ya 1 Andrea

batik satu kali satu kos hijrah Saputra

Jati kos nol berapapun dikalikan 0 = 0

Jadi kalau id gmail.com berapa karena

dia sama Project glass sudutnya hasilnya

adalah nol juga

Hai J dengan Kak sama juga akan Karena

dia sudah kurus Maka hasilnya adalah nol

ingat ya kalau tegak lurus Batita tanya

90-cos nyatanya batik cos60 sama dengan

nol Maka hasilnya pasti Enno gimana dong

kalau saya pengennya yg dengan

ismaya.com kalo yg dengan iman arahnya

sama ya kalau Esa maka media berhimpit

kalau dua garis berhimpit berapa

sudutnya berada sudutnya ya batin nol

sudutnya kalau nol mati kosno itu adalah

satu Nanti kalau nanti i.io J.Co k.ca

itu hasilnya adalah

waktu Kenapa karena antara I dengan

i-tech tanya nol antara jenenge juga

0.km #jawa kos 01 Makanya sini adalah

100 inilah nol ya qq.biz Dota J.Co itu

adalah nol contohnya ya gini ketulis

kehabisan Saya punya Factor kyj tambah

Siska dan telepon sama maka a.by nya

seperti ini gimana ngalirnya kali ini

semuanya ya berarti aksi.id BSI tambah

aksi.co byj + HID zk tambah aye z.co

j.p. BSI tambahan ydhj tambah ayu jqrak

dan seterusnya

Hai tapi ingat Halo Didot kan yang beda

tanda hasilnya nol maka hanya Ginanti

hasil akhirnya kau punya a.de maka sama

dengan hitungan AX caleb's tambah aye

kali BEJ + Z kali BZ Kenapa bisa begini

karena yang perkalian dot beda tandanya

beda arahnya hasilnya adalah nol Ini

sisanya Anda bisa langsung menggunakan

ini saja ya Jadi a.by ya xbx tambah aye

bye tambahan netizen ini adalah

perkalian dot yang hasilnya adalah skala

Oke sekarang kita masuk pada kertas

ilang atau Crash produk dengan simbol

ini ya simbol kali sama siapanya vektor

a

Hai ini vektor B yang biru Cetak adalah

sudut yang diapit oleh kedua kota ini

maka hackrospc itu hasilnya seperti ini

Hai besarnya a kali besarnya B sinus

sudut yang diapit nya kemudian arahnya

nanti ada arahnya adalah across B kita

bahas berlanjut ya Nah secara fisis

operasi cross-product ini adalah

berkaitan dengan sistem yang berputar

atau rotasi

lebih ini adalah anda biasanya kenal

yang namanya aturan tangan kanan kaidah

tangan kanan like Nurul ya Nah hal-hal

seperti itu

Hai yang anda temui ya oh

bersama-bersama fisika yang

ujung-ujungnya ada aturan tangan kanan

berarti secara matematis pasti ada

cross-product ini

Oh ya Jadi kalau saya a.cos kan dengan b

artinya saya dengan tangan kanan saya

arahkan saya putarkan tempat jadi saya

dari a ke b nah jempolnya itu adalah

mengarahkan hasil across banyak Kemana

arahnya ya itu arahnya oke nah Disini

Hai besarnya Bakti absinthe tak arahnya

across B ya Nah untuk koordinat kita xyz

tiga dimensi dari kita ingat bahwa dia

orthogonal harga harus ya derajat

berarti eh antara ini dengan JJ dengan

kakak dengan ini karena biasanya kita

harus Maka nanti nilainya ada sim-nya

sesepuh satu ya kemudian kalau saya

cross-country dengan i-j dengan JK

dengan Kawashima sing berarti sudutnya

0sid no adalah nol nyoba aku ya kalau

saya ikhlas dengan i0g Cross dengan j0k

dengan Kak

Hai Terus bagaimana kalau saya ikhlas

dengan J kemana arah hasilnya Eh pakai

ini kaidah tangan kanan tapi pastikan ya

kalo yg dengan J makan nanti kalau anda

paketan kalian coba Arahkan Pasti

jempolnya mengarah ke milik kalian ke

sumbu z dan Seterusnya saya bisa menekan

ini juga lebih mudahnya ya pijqt ini ada

arah panahnya ya imun jujju Kakao yg

bisa digunakan untuk menentukan arah

Jadi kalau ada yg Cross dengan J Maka

hasilnya adalah Kak je Cross dengan Kak

hasilnya adalah i

Hai Kak Ros dengan Ini hasilnya adalah C

Gimana kalau saya pengen j-cruise

jikalau singa-singa adalah Kak tapi

karena melawan panah Ini hasilnya

negatif jadi Jack Rossi hasilnya adalah

negatif karena melawan arah panah Jadi

kalau saya punya Kak Ros Jack hasilnya

adalah minus ir60 Lawan Arah panah itu

ya Ini percobaannya konsep punya hak

Veto sama b maka begini ya across B yang

menghitung sesuatu ya aksi Cross bxi

tambah X Cross Bridge + X Cross bz1 ya

akhirnya sekarang Age dengan BX aye

dengan byi dengan BZ Ajib dengan bxz

dengan Bridge dengan gadget

Hai tapi ingat yang sama di sini kalau I

dengan isi dengan jika dan Kasihilah

Hai xdx 0y dengan y0 z0 Tinggal dihitung

sisanya Seperti apa kalikan bagian

depannya Tentukan arahnya Oke seperti

itu ya perkalian silang

Hai hey dipakai ini asam pelajari

operasi vektor belajar penjumlahan

secara grafis menjumlah cerah analytic

kemudian perkalian vektor dengan skalar

perkalian vektor dengan Factor baik dot

maupun cross-product sudah anda pelajari

selain ini kita akan bertemu lagi di

video bagian 3 Terima kasih ya