Manual and Automatic PID Tuning Methods | Understanding PID Control, Part 6
Summary
TLDRIn this video, Brian explains PID controller tuning techniques using a mathematical model. He discusses methods like pole placement and loop shaping to adjust the PID controller for optimal system performance. With a linear model, graphical tools in MATLAB like the control system designer app help visually tune the controller. Brian highlights how to avoid pitfalls such as controller saturation and emphasizes the importance of tuning for nonlinear systems. By comparing the responses of different models, he shows how the right tuning can work across multiple system types, providing a deeper understanding of PID control methods.
Takeaways
- 😀 The video explores several methods for PID controller tuning using a mathematical model of the system.
- 😀 With a mathematical model, the PID controller gains can be tuned more systematically compared to manual tweaking.
- 😀 The PID controller operates in both time and S domain, where the focus is on adjusting two zeros and the gain to shape the system's behavior.
- 😀 The video distinguishes between two key PID tuning methods: pole placement and loop shaping.
- 😀 Pole placement involves determining the location of the system's closed-loop poles and adjusting the PID controller to achieve the desired behavior.
- 😀 Loop shaping utilizes frequency response tools like Bode plots to adjust the PID controller to achieve the desired frequency characteristics.
- 😀 Graphical tuning methods using Simulink and control system designer apps allow for real-time adjustment and visualization of PID controller behavior.
- 😀 A key caution is that an ideal PID controller tuning, based on a linear model, may lead to unrealistic performance when applied to nonlinear systems, resulting in saturation or other issues.
- 😀 Automatic PID tuning, provided by software tools, can optimize the controller for better performance while avoiding issues like saturation.
- 😀 The video demonstrates that tuning PID gains using a linearized model can be effective across different models, such as nonlinear models, if the tuning is done correctly.
- 😀 Finally, the video emphasizes that understanding various PID tuning methods enhances the ability to approach system control more effectively in real-world applications.
Q & A
What are the primary steps involved in tuning a PID controller using a mathematical model?
-The primary steps involve first developing a mathematical model of the physical system, then using this model to tune the PID controller by adjusting the proportional (KP), integral (KI), and derivative (KD) gains. These adjustments are made in either the time or frequency domain to achieve the desired system behavior.
Why is using a mathematical model crucial for tuning a PID controller?
-Using a mathematical model allows for more systematic and precise tuning of the PID controller, reducing trial-and-error and the risk of damaging physical hardware. It also provides a deeper understanding of how the PID controller interacts with the system dynamics.
What is the significance of the transfer function in the PID controller?
-The transfer function of the PID controller in the Laplace domain helps identify the location of poles and zeros that determine the system's behavior. By adjusting these, the controller can be fine-tuned to achieve desired performance characteristics such as stability, speed, and accuracy.
What is pole placement in the context of PID controller tuning?
-Pole placement refers to the process of selecting the desired location of the closed-loop poles in a control system. By using the PID controller to adjust the placement of poles, one can shape the system’s dynamic response to meet design specifications.
What role does the root locus play in PID controller tuning?
-The root locus plot helps visualize how the system's poles move as the controller’s gain is varied. By adjusting the placement of zeros and the gain, the root locus can be shaped to position the poles at desired locations, ensuring that the system behaves as intended.
What is loop shaping in PID controller design?
-Loop shaping is a method of adjusting the frequency response of the open-loop system using the PID controller. By manipulating the controller's zeros and gain, the open-loop Bode plot is shaped to achieve desired frequency characteristics, such as gain and phase margin.
How does graphical tuning in the Control System Designer app help with PID tuning?
-Graphical tuning in the Control System Designer app allows users to interactively adjust the zeros of the PID controller and observe the effects on the root locus plot and step response. This provides an intuitive way to understand how the controller parameters affect the system's behavior.
Why is it important to account for saturation in a PID controller?
-Saturation occurs when the controller commands values beyond the physical limitations of the system, such as voltage limits. If not managed, it can lead to performance degradation, such as slow response times or excessive control effort, as seen in the example where the system’s output exceeded the actuator’s capabilities.
What can go wrong when tuning a PID controller without considering actuator limitations?
-When actuator limitations, such as voltage saturation, are not considered during PID tuning, the controller may produce commands that are physically impossible to execute. This can result in a fast response in simulation, but poor real-world performance due to saturation or system instability.
How does automatic PID tuning compare to manual tuning methods?
-Automatic PID tuning offers a more efficient and less error-prone approach by adjusting controller gains based on system behavior. It ensures that the controller operates within the physical limits of the system, unlike manual tuning, where adjustments may inadvertently push the system into undesirable operating conditions.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

3 Ways to Build a Model for Control System Design | Understanding PID Control, Part 5
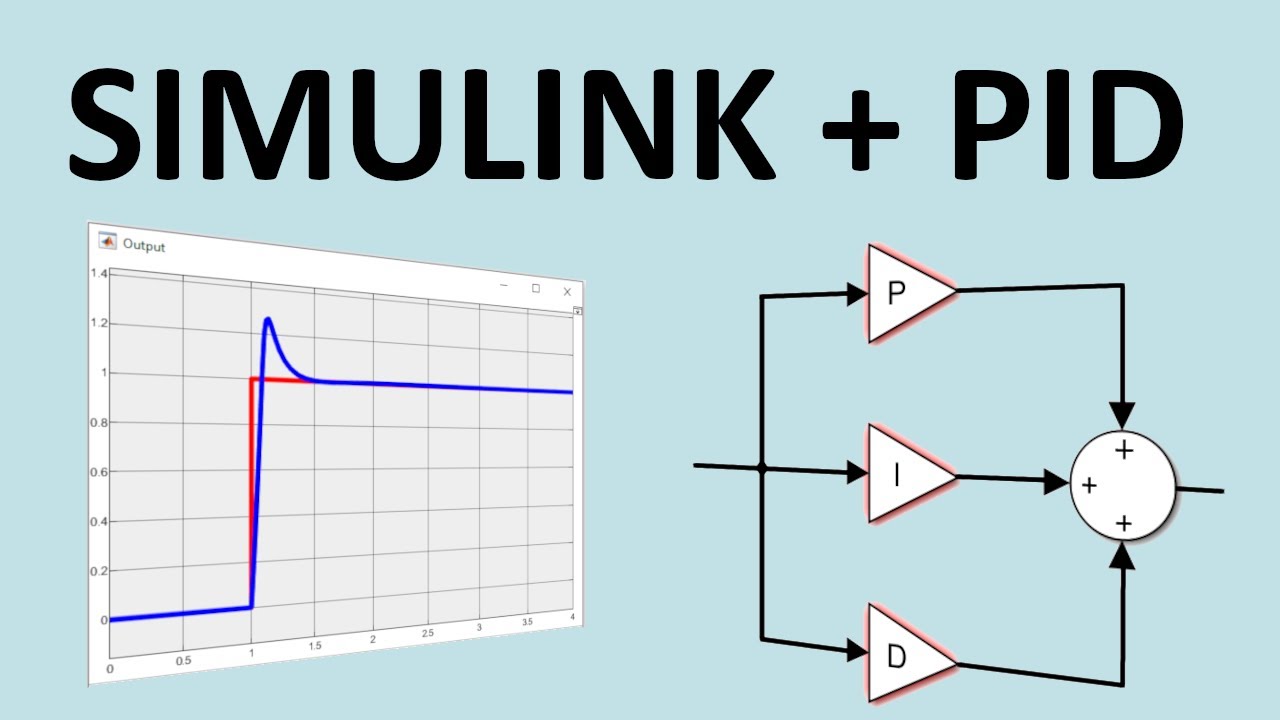
Simulink Control Systems and PID, Matlab R2020b
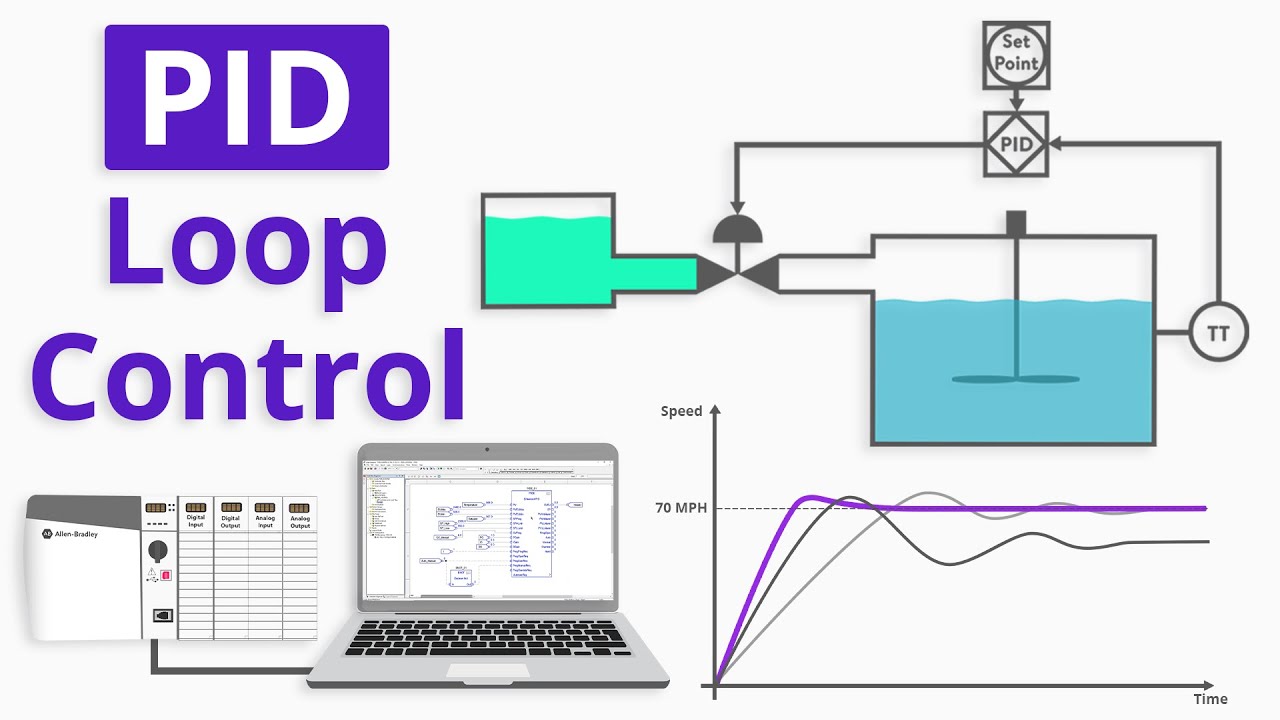
How to Program a Basic PID Loop in ControlLogix

A PID Tuning Guide | Understanding PID Control, Part 4

Tuning PID di Simulink

How To Implement Fuzzy Logic Control in MATLAB/SIMULINK ? (Part-3) | Dr. J. A. Laghari
5.0 / 5 (0 votes)
