Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie

Summary

This educational video explains the key properties and theorems related to right-angled triangles, starting with basic definitions like the legs (catetes) and hypotenuse, and progressing to more advanced concepts. It covers topics such as the properties of isosceles right-angled triangles, the important 30-60-90 theorem, the Pythagorean theorem, and the area of right-angled triangles. Additionally, it touches on concepts like medians and their relation to the hypotenuse, providing clear explanations and practical applications. The video is a valuable resource for students learning geometry, offering useful formulas and insights for solving triangle-related problems.

Takeaways

• 😀 Right-angled triangles have one 90° angle, with the two sides forming this angle called the 'catetes' (legs) and the longest side, opposite the right angle, called the 'hypotenuse'.
• 😀 In an isosceles right-angled triangle, the two legs (catetes) are congruent, and the acute angles opposite the legs are both 45°.
• 😀 If a right-angled triangle has an angle of 30°, the length of the leg opposite this angle is half the length of the hypotenuse (the 30-60-90 triangle theorem).
• 😀 The inverse of the 30-60-90 theorem states that if one leg is half the length of the hypotenuse, the angle opposite that leg must be 30°.
• 😀 The median corresponding to the hypotenuse in a right-angled triangle is always half the length of the hypotenuse.
• 😀 The inverse of the median theorem states that if a median is half the length of the hypotenuse, the triangle must be a right-angled triangle.
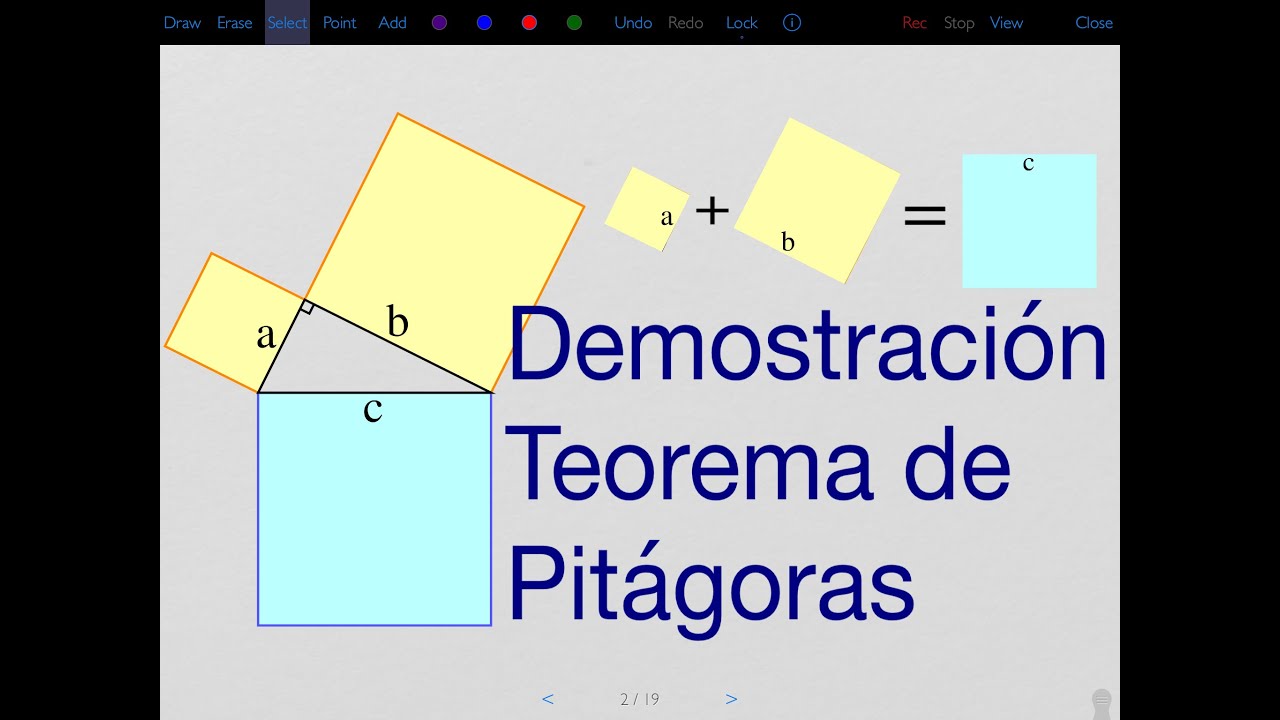
• 😀 The Pythagorean theorem states that in any right-angled triangle, the sum of the squares of the legs equals the square of the hypotenuse (a² + b² = c²).
• 😀 The inverse of the Pythagorean theorem helps determine whether a triangle is right-angled: if the sum of the squares of two sides equals the square of the third side, it is a right-angled triangle.
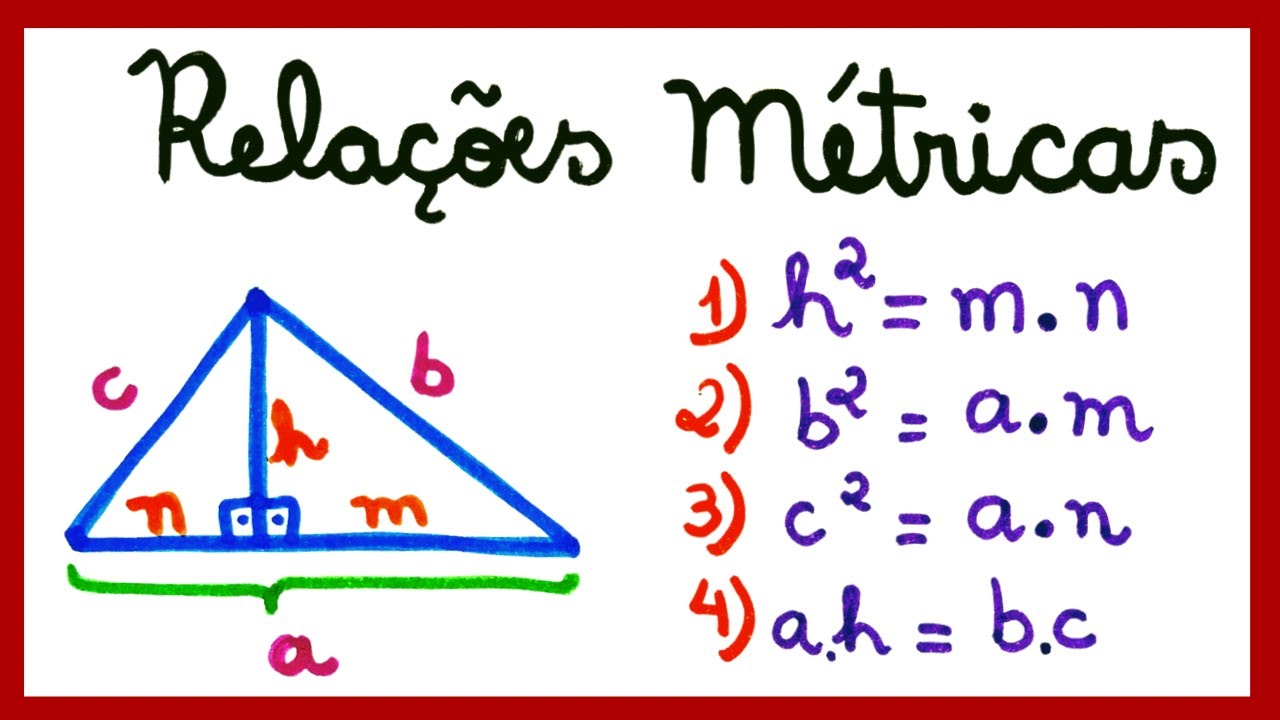
• 😀 The formula for the area of a right-angled triangle is base × height / 2, and this can be calculated using the lengths of the legs.
• 😀 The formula for the height of a right-angled triangle can be derived as one leg × the other leg / hypotenuse, providing a useful way to calculate the height based on the legs and hypotenuse.

Q & A

What is a right triangle?

A right triangle is a triangle that has one angle measuring exactly 90 degrees. This is called the right angle.

What are the legs and the hypotenuse in a right triangle?

In a right triangle, the legs are the two sides that form the right angle, and the hypotenuse is the longest side, which is opposite the right angle.

What is an isosceles right triangle?

An isosceles right triangle is a right triangle where the two legs are of equal length. In this type of triangle, the angles opposite the legs are each 45 degrees.

How can you calculate the angles of an isosceles right triangle?

In an isosceles right triangle, since the sum of all angles in a triangle is 180 degrees, and the right angle is 90 degrees, the remaining two angles must each be 45 degrees.

What does the 30-60-90 triangle theorem state?

The 30-60-90 triangle theorem states that in a right triangle with one angle of 30 degrees, the length of the side opposite the 30-degree angle is half the length of the hypotenuse.

What is the converse of the 30-60-90 triangle theorem?

The converse of the 30-60-90 triangle theorem states that if a right triangle has one leg half the length of the hypotenuse, the angle opposite that leg is 30 degrees.

What does the median theorem for right triangles state?

The median theorem for right triangles states that the length of the median drawn to the hypotenuse of a right triangle is equal to half the length of the hypotenuse.

How do you apply the median theorem in a right triangle?

To apply the median theorem, you need to draw a median from the right angle vertex to the hypotenuse. According to the theorem, the length of this median will be half the length of the hypotenuse.

What is the Pythagorean Theorem and how is it used?

The Pythagorean Theorem states that in a right triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse. It is used to find the length of any side in a right triangle if the lengths of the other two sides are known.

What is the formula for the area of a right triangle?

The formula for the area of a right triangle is (base × height) / 2, where the base and height correspond to the lengths of the two legs of the triangle.