RELATIVITAS KHUSUS - MATERI FISIKA KELAS 12 | Edcent.id

Summary

This video explains the concept of time dilation in Einstein's special relativity, focusing on the effects of relative velocity between observers. It demonstrates how time appears to pass differently for a stationary observer and a moving one. Using examples like the 'twin paradox,' where one twin travels at 0.6c in space and ages slower than the twin on Earth, and a pendulum in space, the video illustrates how velocities close to the speed of light impact the perception of time. The content is aimed at making these complex ideas accessible through practical examples and clear visual explanations.

Takeaways

• 😀 The video explains the concept of special relativity and time dilation.
• 😀 Time dilation occurs when an observer in motion experiences a different passage of time compared to an observer at rest.
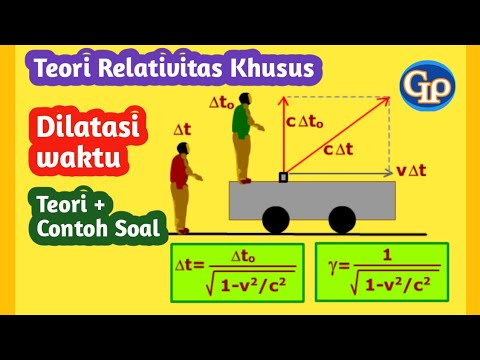
• 😀 The formula for time dilation is Δt = Δt₀ / √(1 - v²/c²), where Δt₀ is the time for the stationary observer, v is the speed of the moving observer, and c is the speed of light.
• 😀 The video uses the example of two twins, A and B, where one twin travels in space at 0.6 times the speed of light and returns to Earth.
• 😀 According to the calculations, twin A, who travels in space, will experience less aging than twin B, who remains on Earth.
• 😀 The relativistic time dilation effect means that twin A will only age 28 years, while twin B ages 35 years during the same period.
• 😀 The video emphasizes that according to special relativity, time flows differently for those moving at high speeds compared to those at rest.
• 😀 A second example explains the dilation of time observed by a pilot in space, who measures a period of 5 seconds for a pendulum with a 3-second period on Earth.
• 😀 The speed of the spacecraft is factored in when calculating the change in the pendulum’s period as observed by the pilot in space.
• 😀 The video concludes with a reminder to activate notifications for future educational videos and invites viewers to visit the website for more learning resources.

Q & A

What is the main topic of the video?

The main topic of the video is 'Time Dilation' as explained through Einstein's theory of special relativity.

What is time dilation?

Time dilation is the phenomenon where time appears to move slower for an observer moving at a high velocity relative to a stationary observer.

Which equation is used to calculate time dilation?

The equation used for time dilation is: Δt = Δt₀ / √(1 - v²/c²), where Δt is the time interval for the moving observer, Δt₀ is the time interval for the stationary observer, v is the velocity, and c is the speed of light.

How does time dilation affect two twins in the 'twin paradox'?

In the twin paradox, one twin travels at a high speed in space, and the other remains on Earth. The traveling twin ages more slowly than the twin who stays on Earth due to time dilation.

What was the velocity of the spaceship in the first example, and how did it affect the time observed by twin A?

The spaceship in the first example was traveling at 0.6 times the speed of light (0.6c). As a result, Twin A, who was traveling in space, experienced 28 years of aging, while Twin B on Earth experienced 35 years.

How do we calculate the age of Twin A when they return to Earth?

The age of Twin A is calculated by applying the time dilation formula. After 35 years for Twin B, the time experienced by Twin A is 28 years. Adding 28 years to the initial age gives Twin A an age of 63 years upon return.

Why does the traveling twin age slower than the stationary twin in the twin paradox?

The traveling twin ages slower because, according to the theory of special relativity, time passes more slowly for objects moving at high velocities relative to a stationary observer.

In the second example, how is the period of the pendulum affected by the velocity of the spaceship?

In the second example, the period of the pendulum on Earth is observed to be longer (5 seconds) by the pilot of a spaceship traveling at 0.8c, due to time dilation.

What is the relationship between the speed of light and the velocity of the spaceship in the second example?

In the second example, the velocity of the spaceship is 0.8 times the speed of light (0.8c). This is used to calculate the time dilation effect on the observed period of the pendulum.

Why do we convert the spaceship's velocity into a fraction of the speed of light (c)?

The velocity is converted into a fraction of the speed of light (c) to simplify calculations and ensure consistency with the units used in Einstein's theory of special relativity.