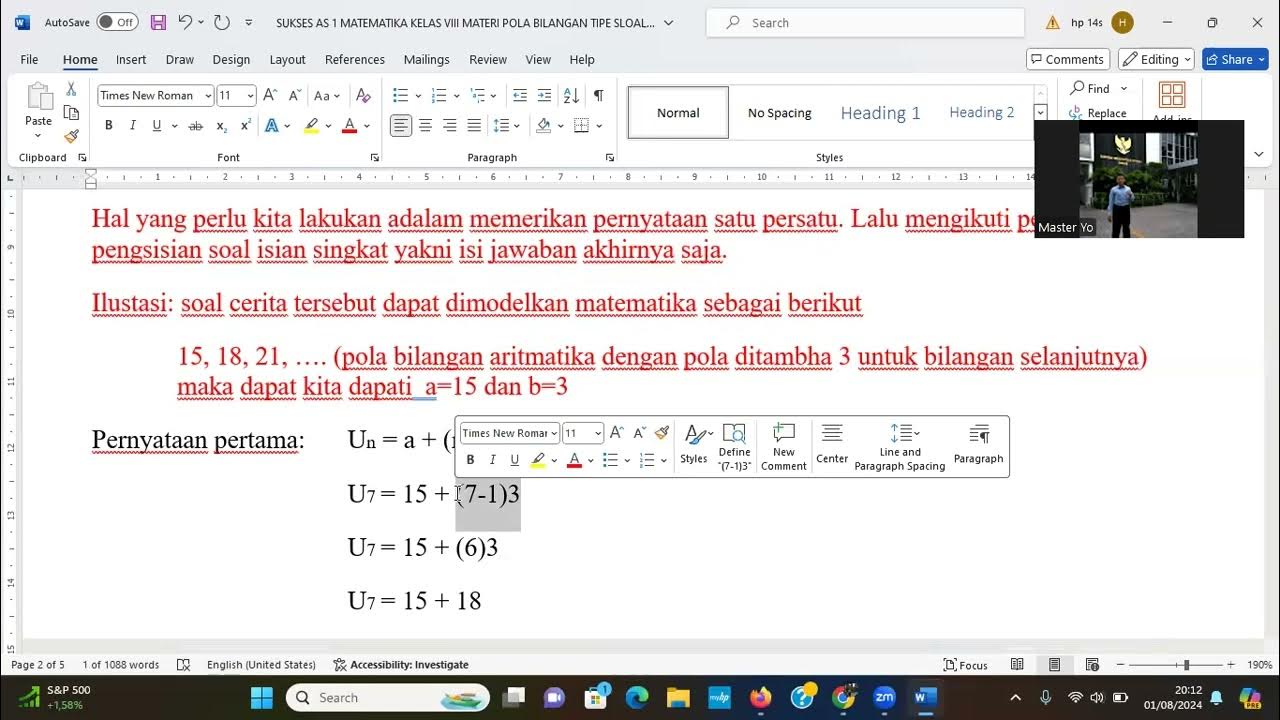
Aula 9 ano - Padrões Simétricos
Summary
TLDRThis educational video focuses on symmetrical patterns, their types, and their application in mathematics. The teacher reviews key concepts like symmetry, reflection, translation, and rotation, which are foundational in understanding geometric designs. Examples include mirror symmetry, translational symmetry (where patterns repeat in multiple directions), and rotational symmetry (where designs remain unchanged when rotated). The video encourages students to explore these concepts further through exercises in their textbooks, aiming to strengthen their understanding of symmetry in various forms.
Takeaways
- 😀 Symmetry patterns in mathematics refer to designs that repeat periodically in multiple directions, also known as mosaics.
- 😀 Symmetry involves harmony resulting from certain regular combinations and proportions.
- 😀 Reflection symmetry, also known as mirror symmetry, occurs when an object’s image is reflected in a mirror, creating identical halves on opposite sides of a line (axis of symmetry).
- 😀 Translational symmetry involves a pattern repeating itself by being moved along a certain distance in a particular direction.
- 😀 Examples of translational symmetry can be seen in mosaics, carpets, and wall designs, where the pattern repeats in a regular, shifting way.
- 😀 Rotational symmetry means that an object’s design remains unchanged as it rotates around an axis, like a sunflower’s petals that stay the same during a 360-degree rotation.
- 😀 In rotational symmetry, objects appear identical no matter how many times they are rotated in a full 360-degree turn.
- 😀 The teacher explains the three types of symmetry: reflection, translation, and rotation, using visual examples like flowers and patterns to demonstrate them.
- 😀 In a given example, the pattern shows all three types of symmetry: mirror symmetry, rotational symmetry, and translational symmetry.
- 😀 The importance of understanding these symmetrical concepts in geometry is highlighted as the students are encouraged to complete exercises on the topic.
Q & A
What are symmetric patterns in mathematics?
-Symmetric patterns, also known as mosaics, are flat drawings that repeat periodically in one or more directions. They are designs that exhibit regularity and can be classified under symmetry in mathematics.
What is symmetry, and how is it defined?
-Symmetry refers to harmony resulting from certain combinations and regular proportions. It implies that proportions within a design are consistent and regular, often involving identical or mirrored elements.
What is reflection symmetry, and how does it work?
-Reflection symmetry, also called mirror symmetry, occurs when one half of an object is a reflection of the other half. A line called the axis of symmetry divides the object into two identical parts that are mirror images of each other.
Can you explain the concept of translation symmetry?
-Translation symmetry happens when a pattern or image repeats itself at a certain distance in multiple directions. It is like shifting the image while keeping it the same, so it repeats seamlessly across a surface.
How is the movement of the Earth related to translation symmetry?
-The movement of the Earth around the Sun is an example of translation symmetry. Just as the Earth moves in a specific path, repeating its position over time, translation symmetry involves repeating patterns or images at a constant distance and direction.
What is rotational symmetry?
-Rotational symmetry refers to an object or pattern that remains unchanged when rotated around a central point. For example, a sunflower's petals exhibit rotational symmetry because their arrangement stays the same even when the flower is rotated.
How does rotational symmetry work in the case of a sunflower?
-In the case of a sunflower, the petals are arranged symmetrically, and their design remains the same regardless of the rotation. When the flower rotates through 360 degrees, the pattern of petals stays consistent, showcasing rotational symmetry.
What are the three types of symmetry discussed in the lesson?
-The three types of symmetry discussed are reflection symmetry (mirror symmetry), translation symmetry (repetition of patterns in a shifted direction), and rotational symmetry (unchanged design through rotation).
How can symmetry be observed in the example of a patterned design?
-In a patterned design, one can observe reflection symmetry (one side mirrors the other), translation symmetry (the design repeats in a shifted manner), and rotational symmetry (the design remains unchanged after rotation).
What is the importance of the axis of symmetry in reflection symmetry?
-The axis of symmetry is the dividing line that separates an object into two mirror-image halves. It is crucial in reflection symmetry because it ensures that the two sides of the object are identical when viewed from opposite directions.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)