DETERMINE LARGEST WEIGHT (W) WHICH CAN BE SUPPORTED BY TWO WIRES|SIMPLE STRESS|STRENGTH OF MATERIALS
Summary
TLDRIn this video, the presenter guides viewers through a solution to a problem involving simple stress and strength of materials. The problem asks for the largest weight that can be supported by two wires with given cross-sectional areas and stress limits. The presenter carefully explains how to calculate the forces and stresses acting on the wires using free body diagrams and equations, demonstrating each step with clear formulas and conversions. The final solution shows that the largest weight that can be safely supported by the wires is 33,462 Newtons. The video also includes shoutouts to viewers who support the channel.
Takeaways
- 😀 Shoutouts are given to viewers, including Daryl Mamaspas and Gerardo Gallopin Jr., with encouragement for others to comment for a chance to be featured.
- 😀 The problem involves determining the largest weight (W) that can be supported by two wires (AB and AC), considering their stress limits and cross-sectional areas.
- 😀 The stress limits for wires AB and AC are given as 100 MPa and 150 MPa, respectively, with corresponding cross-sectional areas of 400 mm² for AB and 200 mm² for AC.
- 😀 The solution requires constructing a free body diagram to clearly visualize the forces acting on the wires, including forces at different angles.
- 😀 Two key equations are derived from the horizontal and vertical force summations: equation 1 for the x-axis and equation 2 for the y-axis.
- 😀 In the x-direction, the force equilibrium equation involves forces in wire AB and AC, with the trigonometric components related to their respective angles.
- 😀 The y-direction equilibrium equation involves the vertical components of forces in wires AB and AC, with the unknown weight (W) to be solved for.
- 😀 Trigonometric functions like sine and cosine are used to simplify and isolate terms for solving the weight supported by the wires.
- 😀 The load supported by wire AC is calculated using stress formulas, converting units from MPa and mm² to N and m², with the final result of 33,462 N for wire AC.
- 😀 The weight supported by wire AB is calculated using similar steps, resulting in 54,640 N for wire AB, but the final supported weight is determined by the smaller value (33,462 N) to avoid exceeding the stress limit on wire AC.
- 😀 The process emphasizes the importance of not exceeding the maximum allowable stress, with the final weight being safely supported by the wire with the lower stress limit, which is wire AC in this case.
Q & A
What is the main topic of the video?
-The main topic of the video is solving a problem related to simple stress under the strength of materials, specifically determining the largest weight (W) that can be supported by two wires (AB and AC) given their stress limits and cross-sectional areas.
What are the stress limits for the two wires?
-The stress limit for wire AB is 100 megapascals, while the stress limit for wire AC is 150 megapascals.
What are the cross-sectional areas of the wires?
-The cross-sectional area of wire AB is 400 square millimeters, and the cross-sectional area of wire AC is 200 square millimeters.
Why is it important to construct a free body diagram?
-Constructing a free body diagram helps to visualize the forces acting on the wires, which is essential for setting up the equations that will be used to solve for the weight the wires can support.
How are the forces on the wires related to the weight (W) to be supported?
-The forces in wires AB and AC are components of the total weight (W) that needs to be supported. The forces are calculated by summing the horizontal and vertical components of the forces acting on the system.
What is the significance of the trigonometric functions in the equations?
-The trigonometric functions like sine, cosine, and tangent are used to resolve the forces into horizontal and vertical components based on the angles of inclination of the wires. This is crucial for solving the equations that determine the maximum weight the wires can support.
What is the formula used to calculate the load carried by wire AC?
-The load carried by wire AC is calculated using the formula: W = AC * (cos(45°) * tan(30°) + sin(45°)), where AC is the load at wire AC, and the formula incorporates the stress limits and cross-sectional area of wire AC.
How is the weight carried by wire AB calculated?
-The weight carried by wire AB is calculated by first isolating the load at AC in the horizontal and vertical force balance equations and then solving for the weight supported by wire AB, considering the stress and cross-sectional area limits of wire AB.
Why do we need to convert units in the calculations?
-Unit conversions are necessary to ensure that the stress is in newtons per square meter (Pa) and the cross-sectional area is in square meters, which are standard units for mechanical calculations. For instance, 1 megapascal (MPa) is converted to 1 million newtons per square meter, and square millimeters are converted to square meters.
What is the final value of the weight supported by the system, and why?
-The final weight supported by the system is 33,462 newtons. This value is chosen because it is the maximum load that can be supported without exceeding the stress limit in wire AC (150 MPa). If the weight were greater, it would exceed the allowable stress for wire AC.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
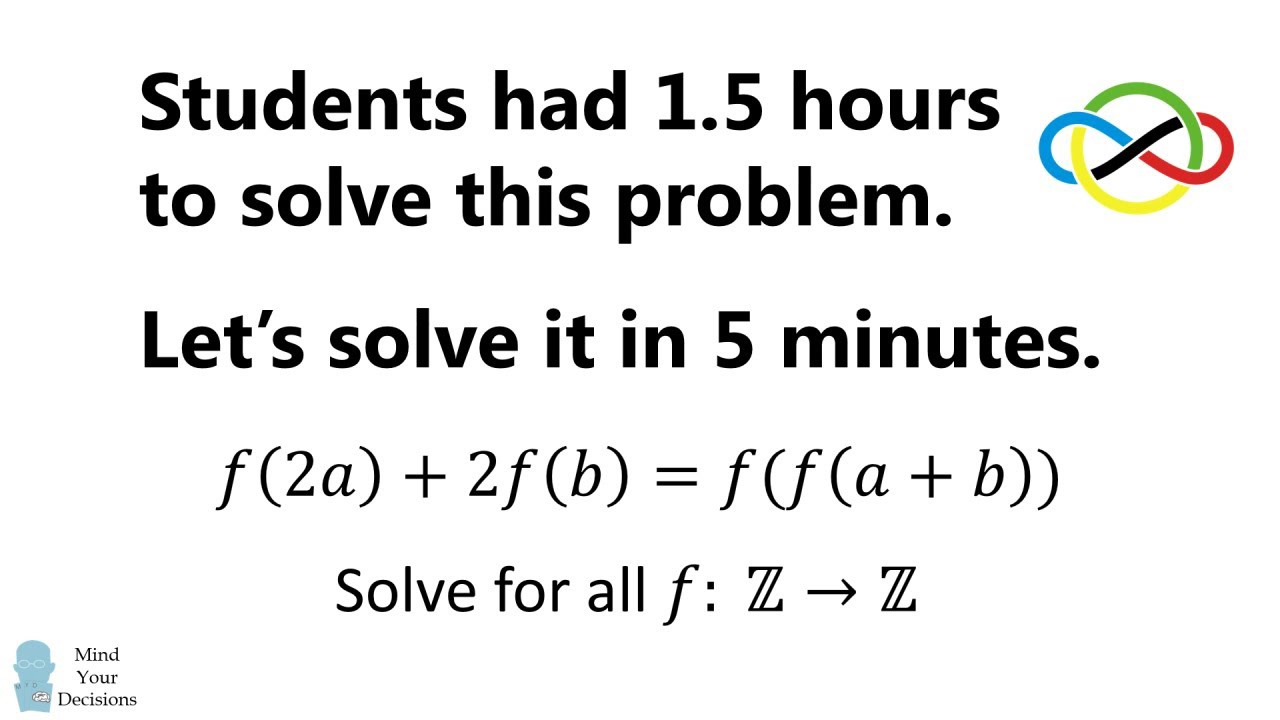
Solving An Insanely Hard Problem For High School Students

Determine internal resultant loading | 1-22 | stress | shear force | Mechanics of materials rc hibb

L3. Longest Substring Without Repeating Characters | 2 Pointers and Sliding Window Playlist

Codeforces Round 839 Div 3 | Problem D: Absolute Sorting Solution | 500 Likes Target | Newton School

Part 2

Can you ? Virtusa Important Coding Questions | Virtusa Online Assessment Test 2025 | Tekno UF
5.0 / 5 (0 votes)
