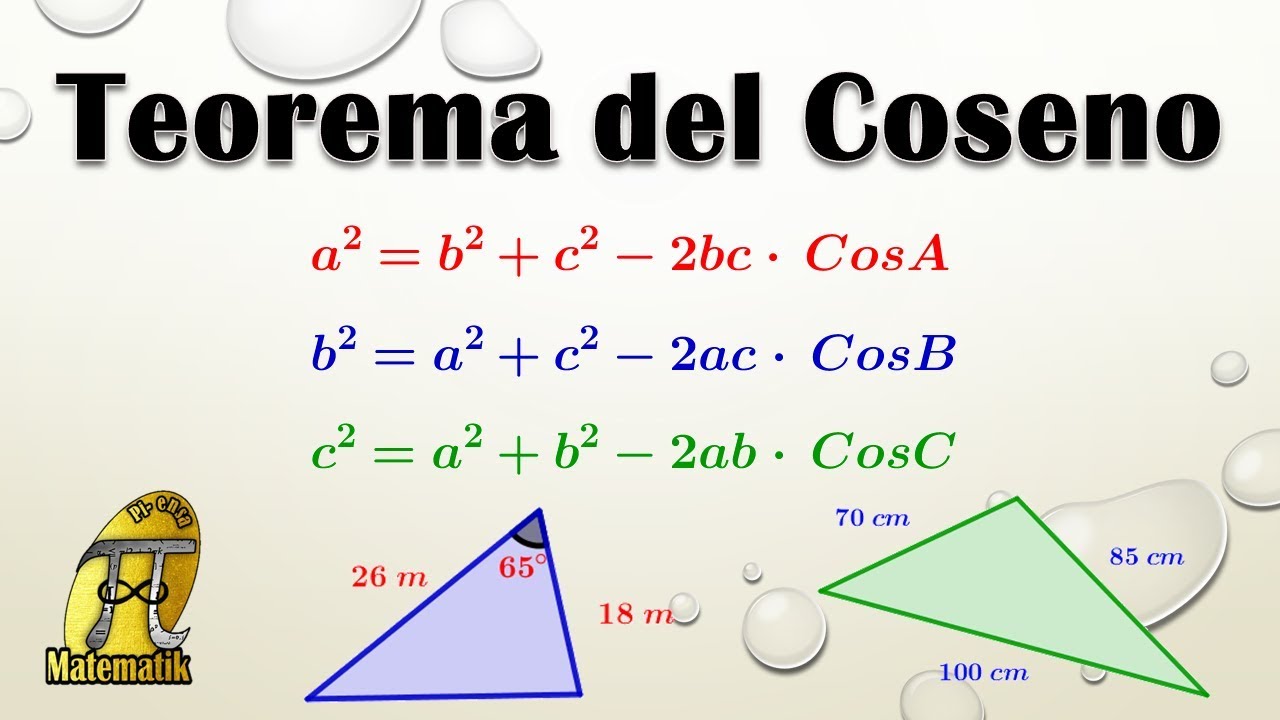
Teorema del coseno - Profesor Maan
Summary
TLDREn este video, el profesor explica de manera detallada el teorema del coseno y cómo se deriva del teorema de Pitágoras. A través de ejemplos prácticos, muestra cómo resolver problemas relacionados con triángulos no rectángulos, donde se conocen dos lados y el ángulo, o las tres longitudes. Además, proporciona estrategias para memorizar la fórmula y aborda tres tipos de problemas clásicos que se pueden resolver aplicando este teorema. El video también ofrece una reflexión sobre los diferentes resultados posibles en algunos problemas y cómo elegir la solución correcta según el contexto del triángulo.
Takeaways
- 😀 El teorema del coseno relaciona los tres lados de un triángulo con el ángulo entre dos de sus lados.
- 😀 Para derivar el teorema del coseno, se parte del teorema de Pitágoras en triángulos rectángulos y se usa trigonometría.
- 😀 La fórmula del teorema del coseno es: c² = a² + b² - 2ab * cos(θ), donde a, b son los lados adyacentes al ángulo θ y c es el lado opuesto.
- 😀 El teorema del coseno generaliza el teorema de Pitágoras, ya que este último es un caso particular cuando el ángulo es recto (90°).
- 😀 Para memorizar la fórmula del teorema del coseno, puedes compararla con la fórmula de la resta al cuadrado: (a-b)² = a² - 2ab + b².
- 😀 El teorema del coseno se usa en tres tipos de problemas: encontrar el tercer lado con dos lados y un ángulo, encontrar un ángulo con tres lados, y encontrar un lado con dos lados y un ángulo no incluido.
- 😀 Un ejemplo simple es usar el teorema del coseno para encontrar el tercer lado de un triángulo con lados a=3, b=2 y ángulo θ=60°.
- 😀 El coseno de 60° es 0.5, lo que facilita el cálculo en problemas del tipo 'buscar el tercer lado'.
- 😀 El teorema del coseno también permite calcular un ángulo interno de un triángulo cuando se conocen los tres lados.
- 😀 En problemas donde se obtiene más de una solución posible (como al resolver una ecuación cuadrática), se debe elegir la respuesta que tenga sentido físico, descartando las longitudes negativas.
Q & A
¿Qué es el teorema del coseno y cómo se deriva?
-El teorema del coseno es una fórmula que relaciona los tres lados de un triángulo cualquiera con uno de sus ángulos. Se deriva del teorema de Pitágoras aplicando triángulos auxiliares y usando identidades trigonométricas. La fórmula es: c² = a² + b² - 2ab * cos(θ), donde a y b son los lados adyacentes al ángulo θ y c es el lado opuesto.
¿Cómo se aplica el teorema del coseno para encontrar un lado cuando se conocen dos lados y el ángulo entre ellos?
-Se utiliza la fórmula del teorema del coseno: c² = a² + b² - 2ab * cos(θ). Solo se debe sustituir los valores conocidos de los lados a, b y el ángulo θ, luego resolver para el valor de c. Este proceso da la longitud del lado opuesto al ángulo dado.
¿Cómo se utiliza el teorema del coseno para encontrar un ángulo conociendo los tres lados de un triángulo?
-Cuando se conocen los tres lados de un triángulo, se reorganiza la fórmula del teorema del coseno para despejar el coseno del ángulo θ: cos(θ) = (a² + b² - c²) / 2ab. Después, se aplica la función arcocoseno para encontrar el valor del ángulo θ.
¿En qué se diferencia el teorema del coseno del teorema de Pitágoras?
-El teorema del coseno es una generalización del teorema de Pitágoras. Mientras que el teorema de Pitágoras solo se aplica a triángulos rectángulos, el teorema del coseno se puede aplicar a cualquier tipo de triángulo, incluso no rectángulos.
¿Cómo se demuestra que el teorema de Pitágoras es un caso particular del teorema del coseno?
-Cuando el ángulo θ es 90 grados, el coseno de 90° es 0, lo que simplifica la fórmula del teorema del coseno a c² = a² + b², que es precisamente el teorema de Pitágoras para triángulos rectángulos.
¿Cuál es una estrategia para memorizar la fórmula del teorema del coseno fácilmente?
-Una estrategia es asociar la fórmula del teorema del coseno con la forma de la diferencia de cuadrados: (a - b)² = a² - 2ab + b². De esta forma, es más fácil recordar que c² = a² + b² - 2ab * cos(θ).
¿Qué significa cuando en un problema aparecen dos soluciones posibles para la longitud de un lado?
-Cuando hay dos soluciones, generalmente una es válida físicamente (positiva) y la otra no lo es (negativa). En problemas de triángulos, siempre se toma la solución positiva, ya que las longitudes de los lados no pueden ser negativas.
En el problema del triángulo con ángulo de 60 grados, ¿cómo se aplica el teorema del coseno para hallar la longitud del lado opuesto?
-Se utiliza la fórmula c² = a² + b² - 2ab * cos(θ), donde a = 3, b = 2 y θ = 60°. Sustituyendo estos valores en la fórmula, se obtiene c² = 3² + 2² - 2 * 3 * 2 * cos(60°), que resulta en c ≈ 2.65.
En el segundo tipo de problema, ¿cómo se calcula el ángulo cuando se conocen las tres longitudes de un triángulo?
-Primero se usa la fórmula del teorema del coseno para despejar cos(θ): cos(θ) = (a² + b² - c²) / 2ab. Luego se calcula el valor de cos(θ) con los valores numéricos de los lados y se utiliza la función arcocoseno para encontrar el ángulo θ.
¿Por qué es importante comprender la relación entre los lados y los ángulos de un triángulo al usar el teorema del coseno?
-Entender esta relación es clave para aplicar correctamente el teorema del coseno en la resolución de problemas de geometría, ya que permite usar los valores conocidos de los lados y los ángulos para encontrar los valores desconocidos, ya sean lados o ángulos, de manera precisa.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)