Inequalities | Tagalog Tutorial Video
Summary
TLDRIn this math tutorial, Kat explains how to solve and graph inequalities, focusing on the use of symbols like less than, greater than, and their respective variations. Through step-by-step examples, Kat demonstrates how to solve inequalities like 3x < 5, 2x - 1 > 1, and -4x ≤ -8, guiding viewers on how to isolate variables and represent solutions on a number line. The video also covers interval notation and the difference between open and closed circles. A clear and practical lesson for anyone looking to grasp the basics of solving inequalities.
Takeaways
- 😀 Understand the basic inequality symbols: '<' (less than), '>' (greater than), '≤' (less than or equal to), and '≥' (greater than or equal to).
- 😀 Inequalities describe relationships between two expressions, showing ranges of values for a variable.
- 😀 Solving inequalities often involves isolating the variable on one side of the inequality sign.
- 😀 When graphing an inequality on a number line, an open circle indicates that the boundary value is *not* included in the solution.
- 😀 A closed circle on the number line means that the boundary value *is* included in the solution.
- 😀 If you multiply or divide both sides of an inequality by a negative number, you must flip the inequality sign.
- 😀 Interval notation is used to express ranges of values, where '(-∞, 3)' represents values less than 3 and '[2, ∞)' represents values greater than or equal to 2.
- 😀 Solving the inequality '3x < 9' results in 'x < 3', which can be graphed with an open circle at 3.
- 😀 The inequality '2x - 1 > 1' can be solved to find 'x > 1', which is represented on a graph with an open circle at 1 and shading to the right.
- 😀 In the example '-4x ≤ -8', dividing by -4 flips the inequality, resulting in 'x ≥ 2', which is graphed with a closed circle at 2 and shading to the right.
Q & A
What is the main topic of the video?
-The main topic of the video is explaining mathematical inequalities, including how to solve them and represent them on a number line.
What are the key inequality symbols discussed in the video?
-The key inequality symbols discussed are 'less than', 'greater than', 'less than or equal to', and 'greater than or equal to'.
What does the video demonstrate with the example '3x is less than'?
-The video demonstrates how to represent the inequality '3x is less than a value' on a graph, specifically using a number line.
How does the video solve the inequality '2x - 1 is greater than 1'?
-The video solves this inequality by first isolating 'x', then dividing both sides by 2, leading to the solution x > 1.
What does the graph look like for the inequality 'x > 1'?
-The graph for the inequality 'x > 1' will show an open circle at 1 on the number line, indicating that 1 is not included, and a shaded region to the right of 1.
What is the result when solving the inequality '-4x is less than or equal to -8'?
-The result is x ≥ 2. After dividing both sides by -4 (and reversing the inequality because of dividing by a negative number), the solution is x ≥ 2.
Why is the inequality reversed when dividing by a negative number?
-The inequality is reversed when dividing by a negative number because multiplying or dividing by a negative value flips the direction of the inequality.
What does the number line for the inequality 'x ≤ 2' look like?
-The number line for 'x ≤ 2' will have a closed circle at 2, indicating that 2 is included in the solution, with the shaded region extending to the left of 2.
What does the speaker mean when they refer to 'interval notation'?
-Interval notation is a way to express the solution to an inequality using intervals. For example, 'x ≥ 2' would be written as [2, ∞) in interval notation.
How does the speaker encourage engagement with the channel at the end of the video?
-At the end of the video, the speaker encourages viewers to subscribe to the channel for more content and thanks them for watching.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

ILLUSTRATING LINEAR INEQUALITIES IN TWO VARIABLES || GRADE 8 MATHEMATICS Q2
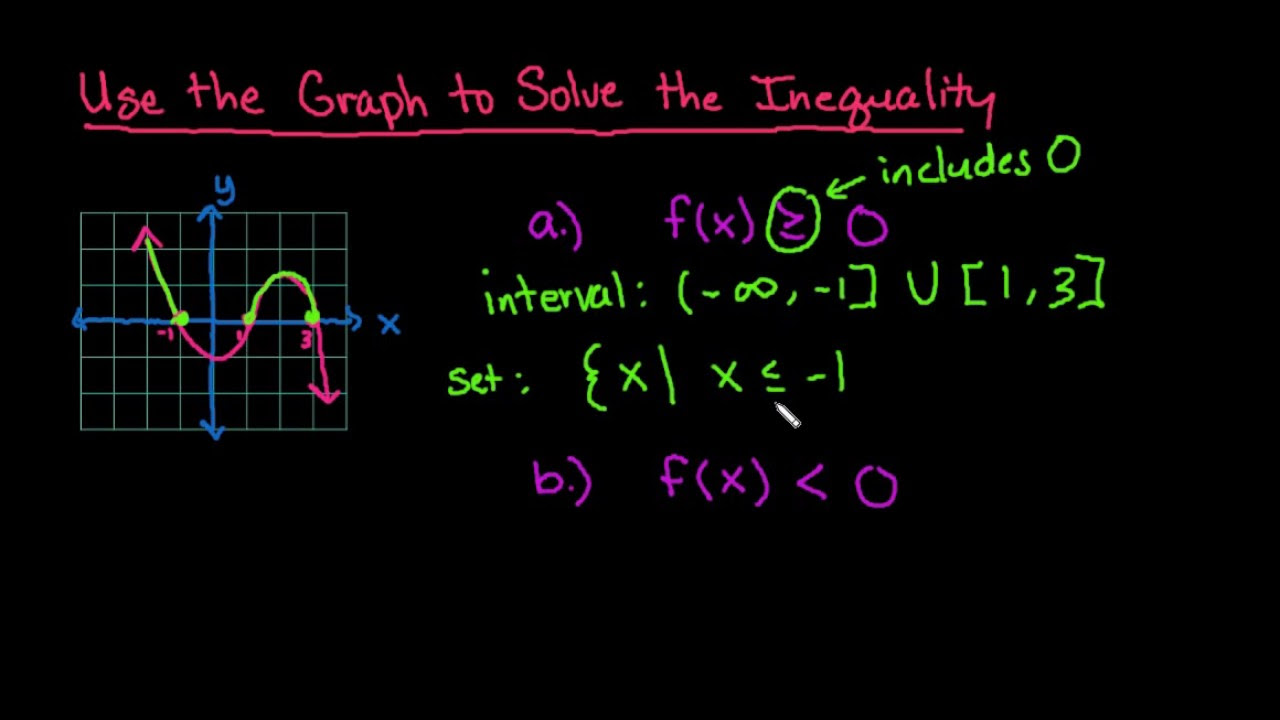
Solve a Polynomial Inequality Graphically

Express Inequalities as a Graph and Interval Notation
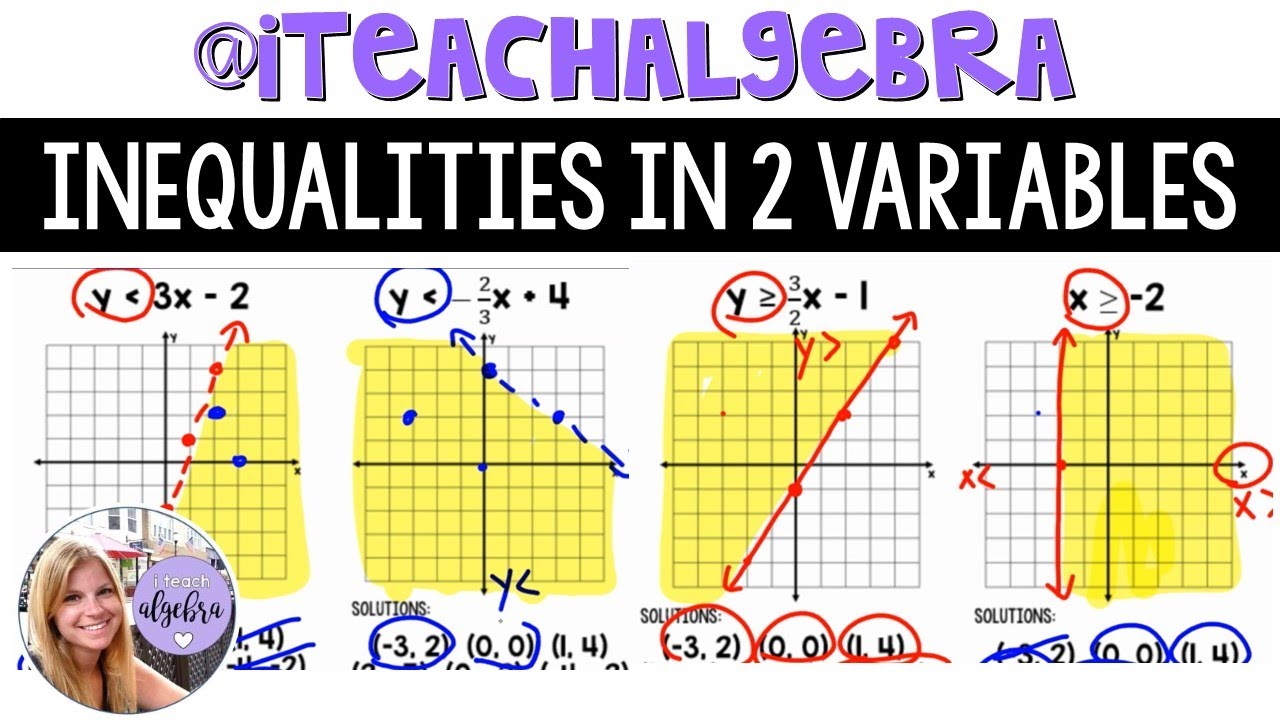
Algebra 1 - Graphing Inequalities in Two Variables
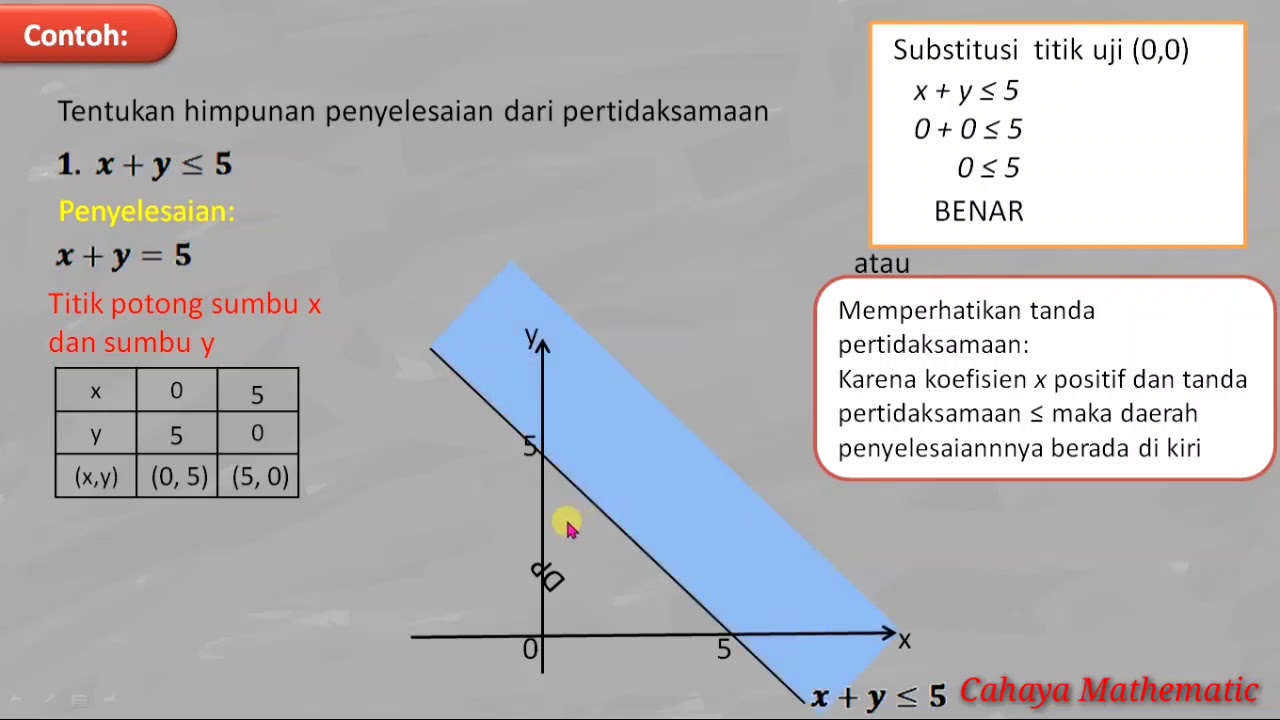
PERTIDAKSAMAAN LINEAR DUA VARIABEL
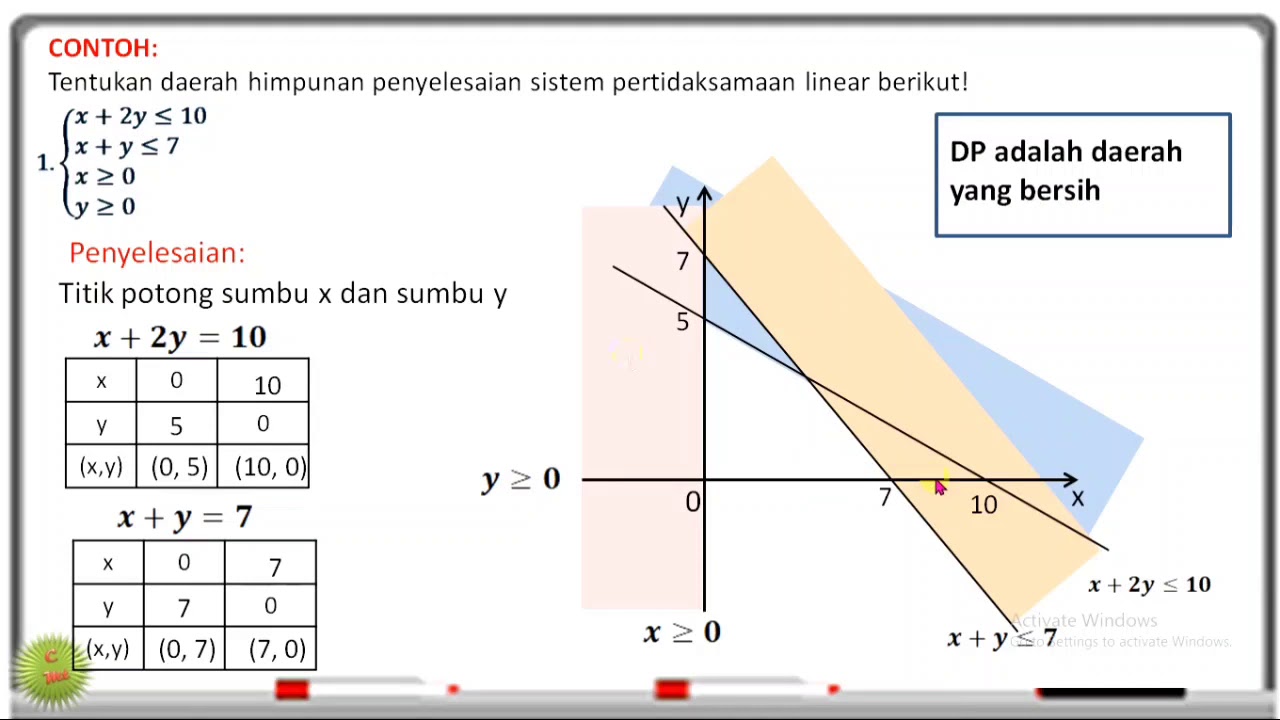
SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL SPtLDV
5.0 / 5 (0 votes)
