Express Inequalities as a Graph and Interval Notation

Summary

This video script offers a detailed tutorial on graphing and expressing inequalities in interval notation. It explains how to plot points for various inequalities, including less than, greater than, and less than or equal to, using open and closed circles to indicate inclusion or exclusion of endpoints. The script also demonstrates how to graph compound inequalities and provides examples of interval notation for each scenario, clarifying the use of parentheses and brackets for different cases.

Takeaways

• 📊 When graphing inequalities, use an open circle for values not included in the interval and a closed circle for values that are included.
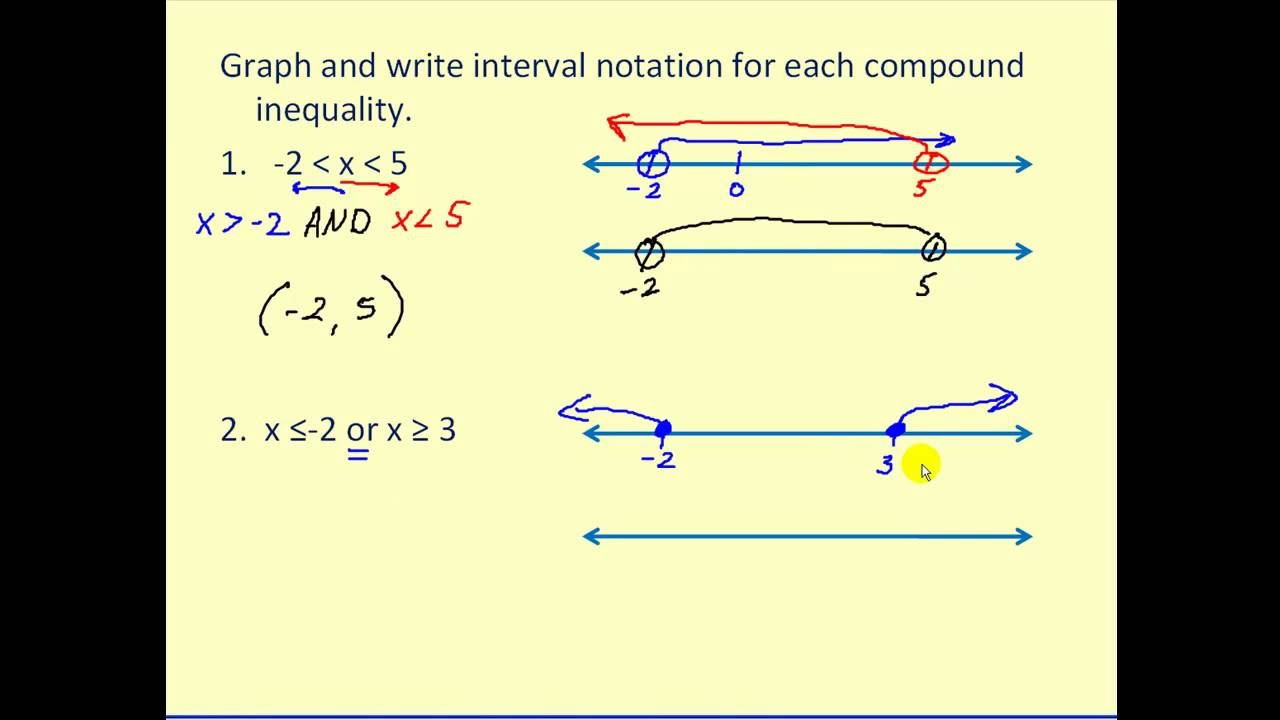
• 🔍 For inequalities like 'X less than five', graph to the left of the number five, approaching negative infinity, and use parentheses to denote exclusion.
• 📌 Interval notation for 'X less than five' is written as "(-∞, 5)", indicating values less than five but not including five itself.
• 📈 For 'X greater than negative two', graph to the right of negative two, approaching positive infinity, and use parentheses to show exclusion of negative two.
• 🌐 The interval notation for 'X greater than negative two' is "(-2, ∞)", showing all values greater than negative two.
• 🔄 When an inequality includes an endpoint, like 'X less than or equal to negative one', use a square bracket to indicate inclusion.
• ⚠️ For 'X equals three', the interval notation can be expressed as "[3, 3]", showing that only the number three is included in the interval.
• 🔑 In interval notation, 'X greater than or equal to two' is written as "[2, ∞)", including two and extending to positive infinity.
• 🔄 For compound inequalities, like 'X greater than or equal to negative three and less than four', graph between the two values with appropriate inclusion or exclusion.
• 📐 The interval notation for the compound inequality 'X greater than or equal to negative three and less than four' is "[-3, 4)", including negative three but not four.
• 📉 For 'X greater than negative eight and less than or equal to zero', the interval does not include negative eight but does include zero, shown as "(-8, 0]" in interval notation.

Q & A

What does an open circle on a number on a graph represent in the context of inequalities?

An open circle on a number on a graph represents that the number is not included in the interval of the inequality.

How is the interval for the inequality 'X less than five' represented in interval notation?

The interval for 'X less than five' is represented in interval notation as '(-∞, 5)', indicating all values less than five, not including five itself.

What is the difference between a closed point and an open point on a graph when dealing with inequalities?

A closed point on a graph indicates that the value is included in the interval of the inequality, while an open point indicates that the value is not included.

How do you express the interval for 'X greater than negative two' in interval notation?

The interval for 'X greater than negative two' is expressed in interval notation as '(-2, ∞)', including all values greater than negative two, but not including negative two itself.

What is the interval notation for 'X less than or equal to negative one'?

The interval notation for 'X less than or equal to negative one' is '[-∞, -1]', including all values less than or equal to negative one.

How is the single value interval for 'X equals three' represented in interval notation?

The single value interval for 'X equals three' can be represented in interval notation as '[3, 3]', indicating that only the value three is included in the interval.

What does a closed point on a number signify when graphing the inequality 'X greater than or equal to two'?

A closed point on a number signifies that the number is included in the interval of the inequality, so for 'X greater than or equal to two', a closed point is made at two.

How do you express a compound inequality like 'negative three less than or equal to X less than four' in interval notation?

A compound inequality like 'negative three less than or equal to X less than four' is expressed in interval notation as '[-3, 4)', including negative three but not including four.

What is the interval notation for the inequality 'negative eight less than X less than or equal to zero'?

The interval notation for 'negative eight less than X less than or equal to zero' is '(-8, 0]', including zero but not including negative eight.

How do you determine whether to use a square bracket or a rounded parenthesis when expressing intervals involving infinity?

When expressing intervals involving infinity, a rounded parenthesis is always used. For finite endpoints that are included in the interval, a square bracket is used; if the endpoint is not included, a rounded parenthesis is used.

Can the interval notation for a single value be expressed using set notation?

Yes, the interval notation for a single value can also be expressed using set notation by placing the value within braces, such as '{3}' for the interval '[3, 3]'.