Matrices for General Linear Transformations | Linear Algebra
Summary
TLDR本视频讲解了线性变换与矩阵表示的关系。通过引入基向量和坐标向量,阐述了如何使用矩阵来表示和计算线性变换。具体包括了从向量空间V到W的线性变换,通过找出V的基向量在W中的像,并构建转换矩阵,最终使用矩阵乘法来实现变换。通过实例展示了如何将多项式空间的线性变换转化为矩阵表示,并说明了不同基下的变换矩阵如何影响变换结果。视频进一步探讨了计算机如何有效地利用矩阵运算进行线性变换。
Takeaways
- 😀 线性变换可以通过矩阵表示,每个有限维线性变换都可以用矩阵表示。
- 😀 给定向量空间V和W,以及V到W的线性变换T,我们可以通过选择合适的基来找到T的矩阵表示。
- 😀 线性变换的矩阵表示依赖于域和余域的基,并且基的选择会影响最终的矩阵形式。
- 😀 对于每一个线性变换,可以通过将基向量的变换结果作为矩阵的列来构建矩阵。
- 😀 通过矩阵乘法,我们可以快速地实现线性变换,从而简化计算过程。
- 😀 计算矩阵时,需要通过查找每个基向量在变换下的映射来得到矩阵的每一列。
- 😀 在构造矩阵时,首先需要找出基向量的变换结果,并将这些变换结果表示为新基下的坐标向量。
- 😀 例如,通过选择适当的标准基来描述变换,我们可以通过矩阵与坐标向量的乘积来实现变换。
- 😀 线性变换的矩阵不仅限于标准基,其他非标准基也可以用来表示相同的线性变换,但矩阵形式会有所不同。
- 😀 线性变换的矩阵使得计算变换变得更加方便,尤其在计算机科学中,矩阵乘法可以有效地实现变换。
- 😀 在应用变换时,我们可以通过将任意向量写成其坐标向量,并用变换矩阵乘以该坐标向量来得到变换后的结果。
Q & A
什么是线性变换矩阵?
-线性变换矩阵是一个表示线性变换的矩阵,通过该矩阵可以将向量从一个向量空间映射到另一个向量空间。这个矩阵的列由基向量的变换结果构成。
如何通过矩阵表示线性变换?
-通过选择适当的基,首先确定线性变换在这些基向量上的映射,然后将这些映射结果的坐标向量作为矩阵的列来表示线性变换。
如何构造线性变换的矩阵?
-构造线性变换矩阵的步骤是找到基向量的映射,并计算它们相对于目标基的坐标向量。然后将这些坐标向量作为列来组成矩阵。
线性变换矩阵是如何与向量相乘的?
-将向量的坐标向量与线性变换矩阵相乘,结果是变换后的向量的坐标向量。然后可以通过这个坐标向量找到变换后的向量。
为什么要使用矩阵来表示线性变换?
-使用矩阵表示线性变换能够简化计算过程,尤其是在计算机中,矩阵乘法比直接计算变换更高效。
在不同的基下,线性变换的矩阵是否相同?
-不相同。线性变换的矩阵依赖于选择的基,不同的基会导致不同的矩阵表示。
如何确定变换矩阵相对于特定基的表示?
-通过将线性变换作用于基向量,找出变换后的向量,然后将这些向量相对于目标基的坐标作为矩阵的列。
如何将P1到P2的变换用矩阵表示?
-通过计算P1中基向量(如1和x)在P2中的映射,得到这些映射的坐标向量,最后将这些坐标向量作为矩阵的列,形成表示该变换的矩阵。
为什么线性变换的矩阵需要相对于基来计算?
-因为基向量的选择决定了线性变换如何作用于整个向量空间。不同的基会影响变换后的坐标表示,从而影响矩阵的形式。
给定一个线性变换矩阵,如何计算任意向量的变换结果?
-将该向量表示为相对于基的坐标向量,然后与线性变换矩阵相乘,得到变换后向量的坐标,最后通过坐标向量确定变换后的实际向量。
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Using Linear Models for t tests and ANOVA, Clearly Explained!!!

Introduction to linear independence | Vectors and spaces | Linear Algebra | Khan Academy
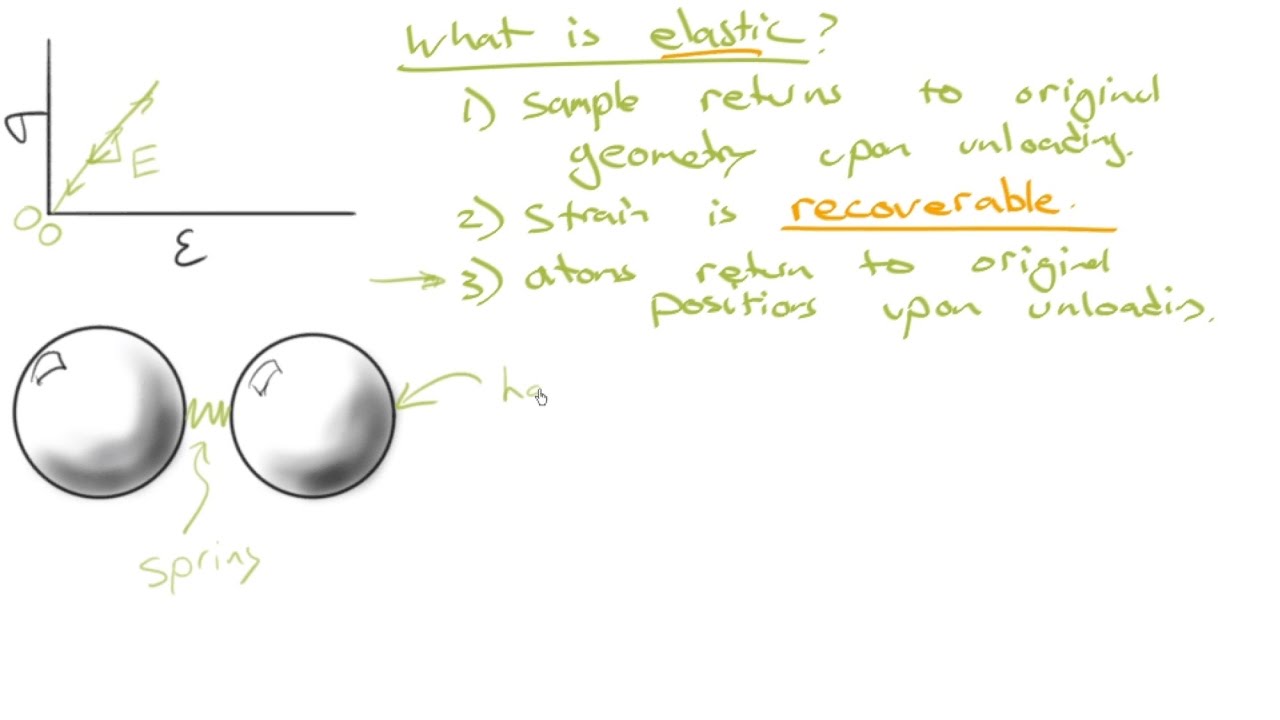
04 Atomic Definition of Young's Modulus

Intro to the Laplace Transform & Three Examples

STAT115 Chapter 10.1 Transcription Regulation

What Is Entity Relationship Diagram ( ERD ) | ER Model Explained In DBMS With Examples

Integración por sustitución | Ejemplo 16 | Seno cuadrado por coseno
5.0 / 5 (0 votes)
