Third detailed example: Control input
Summary
TLDRThis video explains how to build a linear model using a black box approach, focusing on spring elongation under different weights in two labs. Despite the labs using similar springs, they may show different behaviors due to slight differences in the springs' lengths. The video demonstrates how to account for these differences by considering both weight (a continuous variable) and lab (a categorical variable) as inputs in the model. The challenge is to merge data from the two labs into a single dataset for analysis, using appropriate statistical methods to capture the effect of both lab and weight on spring elongation.
Takeaways
- 😀 The black box approach helps simplify the modeling of systems where input-output relationships are known, but internal mechanisms are not fully understood.
- 😀 This scenario involves two types of springs from different labs that are similar in material and geometry but differ slightly in length.
- 😀 The aim of the study is not to focus on the differences between labs but to study the elastic behavior of the springs in response to applied weight.
- 😀 In the black box model, there are two inputs: weight (a continuous variable) and lab (a categorical variable indicating the origin of the spring).
- 😀 The output of the model is the length of the spring, which changes depending on the weight applied, and the data is collected from two different labs.
- 😀 Labs may use different sets of weights for their measurements, and some measurements may be repeated to account for random error.
- 😀 Repeated measures are common in practical experiments to assess variability due to random factors.
- 😀 Data from the two labs may be collected in separate files, but to analyze them together, the data must be merged into a single data set.
- 😀 Software like R requires a unified data set to perform analysis, so it is essential to combine measurements from different labs into one format.
- 😀 The main challenge is not dealing with random errors or small differences between labs, but rather how to model these differences and combine data effectively.
Q & A
What is the central objective of the video script?
-The video explores the process of creating a linear model using a black box approach to study the elastic behavior of springs. The focus is on dealing with data from two different labs, considering both the weight and lab as factors affecting the spring's elongation.
What are the two types of springs mentioned in the video, and why are they important?
-The two springs are made from the same material and geometry, but differ in length. This difference is important because the script aims to study the elastic behavior of the springs while accounting for the lab-specific differences, which should not be ignored.
Why is the 'lab' factor considered in the model?
-The 'lab' factor is considered because different labs may introduce unique variables, even if they work with similar materials. The aim is to control for these differences, which might influence the outcome (spring length), and include it as a categorical input in the model.
What does the 'black box' approach refer to in the context of the video?
-The 'black box' approach refers to a method where the internal workings of the spring (its elastic properties) are abstracted. The inputs (weight and lab) are used to predict the output (length) without directly investigating the internal characteristics of the spring.
How is data from two labs handled in the analysis?
-Data from two labs are handled by merging them into one dataset. This involves adding a column to indicate the lab and then combining the data into a single file, ensuring that both weight and length variables align correctly for analysis.
Why might the weights differ between the two labs?
-The weights used in each lab may differ because each lab might select different sets of measurements. Additionally, some weights might be repeated in a single lab to account for random errors and variability in the measurements.
What statistical model is used to analyze the data?
-A linear model is used, where weight and lab are both included as predictors. The model also accounts for the interaction between weight and lab, helping to understand how these factors influence the spring's length.
What is the significance of including the interaction term in the linear model?
-Including the interaction term between weight and lab allows the model to explore whether the relationship between weight and spring length differs depending on the lab. This helps identify if lab-specific factors influence the effect of weight on the spring's elongation.
How does the repeated measure experiment affect the analysis?
-In a repeated measure experiment, the same weight is applied multiple times, helping to account for random error and increasing the reliability of the results. This approach provides a more accurate estimate of the relationship between weight and spring length.
What role does the lab variable play in determining the spring's behavior?
-The lab variable helps to capture any systematic differences between labs that might affect the spring's behavior. These differences could arise from variations in equipment, handling, or environmental factors that could influence the measurements of the spring's length.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Percobaan Eksperimen Hukum Hook (Hooke's Law Experiment) | Praktikum Fisika Dasar 1

PIPOL 4 - Model Kotak Hitam dan Bola Lampu

Il comportamento elastico di una molla (tratto da Fisica in laboratorio et al)

Praktikum Fisika 1 Getaran pada Pegas (Modul 7)
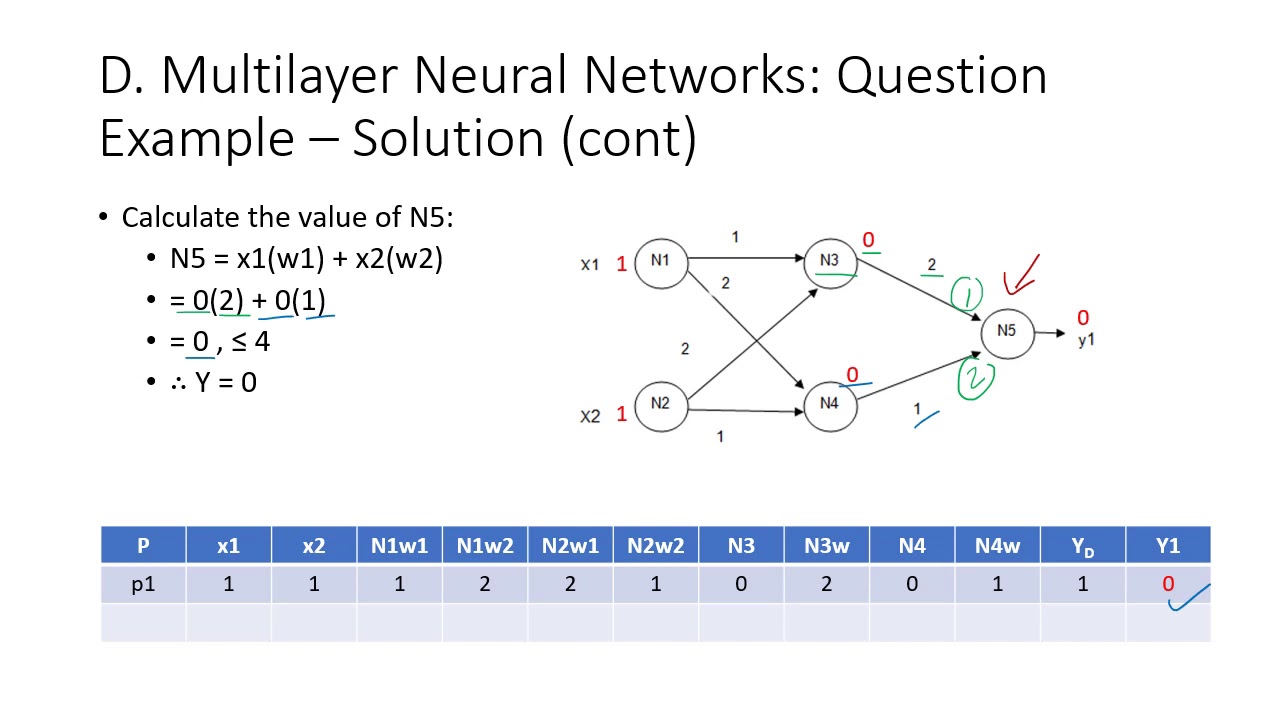
Topic 3D - Multilayer Neural Networks

Pengantar NN DL #2 The Perceptron
5.0 / 5 (0 votes)
