PROGRAM LINIER - METODE GRAFIK - RISET OPERASI
Summary
TLDRThis educational video explains how to solve linear programming problems using the graphical method. It covers the foundational concepts of linear programming, including decision variables, objective functions, and constraints. The video also highlights the assumptions underlying linear programming, such as proportionality, additivity, divisibility, and determinism. Through a practical example, the video demonstrates how to formulate a linear programming problem for a pottery company, maximize profits, and graphically solve for optimal solutions. The tutorial emphasizes the importance of understanding variables, constraints, and the graphical interpretation of solutions to optimize resource allocation effectively.
Takeaways
- 😀 Linear programming is a model used for solving optimization problems, especially in allocating limited resources optimally.
- 😀 The key components of linear programming include decision variables, objective functions, and constraints.
- 😀 Decision variables in a linear programming problem are represented as symbols (e.g., x1, x2) that denote quantities to be optimized.
- 😀 The objective function in linear programming is aimed at maximizing or minimizing a certain value, like profit or cost.
- 😀 Constraints represent the limitations or resources available, such as labor hours or raw material quantities, and are expressed as inequalities.
- 😀 Assumptions in linear programming include proportionality, additivity, divisibility, and determinism.
- 😀 Proportionality means that changes in the decision variables lead to proportional changes in the objective function and resource usage.
- 😀 Additivity ensures that the effects of individual activities are independent, allowing for the summation of their contributions.
- 😀 Divisibility implies that the output and input quantities in linear programming can be fractional or continuous.
- 😀 The graphical method is used to solve linear programming problems with two variables, where constraints and objective functions are visualized on a graph.
- 😀 In the graphical method, the feasible region is the area where all constraints are satisfied, and the optimal solution is found by evaluating the objective function at the vertices of this region.
Q & A
What is linear programming?
-Linear programming is a mathematical model used for optimizing the allocation of limited resources to various activities. It helps to maximize profit or minimize cost while adhering to certain constraints.
What are the basic assumptions in linear programming?
-The basic assumptions in linear programming include proportionality (where changes in output are proportional to input changes), additivity (where the contribution of each activity is independent), divisibility (where outputs can be fractional), and determinism (where all parameters are known with certainty).
What are decision variables in linear programming?
-Decision variables are the unknowns in a linear programming problem that represent the quantities to be determined. In the given example, they represent the number of bowls (X1) and cups (X2) to be produced.
What is the role of the objective function in linear programming?
-The objective function in linear programming defines the goal of the optimization, either to maximize profit or minimize costs. In the example, the objective function is to maximize profit from producing bowls and cups.
What are constraints in linear programming?
-Constraints are limitations or restrictions in a linear programming problem that define the feasible region. They typically represent resource limitations like time, materials, or labor, and are expressed as inequalities.
Why is the graphical method used in linear programming?
-The graphical method is used for solving linear programming problems with two decision variables. It involves plotting the constraints and finding the feasible region, then using the objective function to identify the optimal solution.
What does 'feasible region' mean in linear programming?
-The feasible region in linear programming is the area on the graph where all constraints are satisfied. This is the set of possible solutions from which the optimal solution is chosen.
How do you find the optimal solution in the graphical method?
-To find the optimal solution, you plot the constraints as lines on a graph, identify the feasible region, and then evaluate the objective function at each corner (vertex) of the feasible region. The solution with the highest or lowest value of the objective function is the optimal solution.
What is the significance of the slack variables in linear programming?
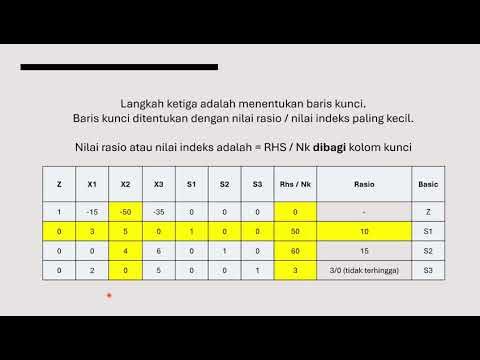
-Slack variables are introduced to transform inequality constraints into equalities. They represent unused resources in a linear programming problem and help to easily solve the system of equations.
What does it mean to 'maximize profit' in the context of this linear programming example?
-In this context, maximizing profit means determining the number of bowls (X1) and cups (X2) that should be produced each day in order to achieve the highest possible profit, considering the limited resources of labor and clay.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Linear Programming - Graphical Solution | Don't Memorise

MK Kuantitatif - Linier Programming Metode Simpleks

Ch04 Linear Programming

Menyelesaikan Permasalahan Program Linear Menentukan Nilai Optimum dengan Metode Uji Titik Pojok

Linear Programming dengan Metode Grafik
Metode Simplex dengan 3 Variable - Riset Operasional
5.0 / 5 (0 votes)
