01 - Fluid Transport - Pitot Tube
Summary
TLDRIn this video, the speaker explains the principles behind the Pitot tube, a device used to measure fluid velocity. The tutorial covers important fluid dynamics concepts, including Bernoulli’s equation, hydrostatic pressure, and manometer readings. Key steps for calculating velocity and flow rate are discussed, with a focus on assumptions, simplifications, and the correction factors needed for accurate results. The speaker also highlights the significance of fluid density and surface area in the equations, offering a comprehensive overview of how to use the Pitot tube for fluid measurements in real-world applications.
Takeaways
- 😀 The video introduces the concept of a Pitot tube, which is used to measure fluid velocity in pipes.
- 😀 The presenter explains the schematic diagram of a Pitot tube system and its components, such as the manometer and mercury fluid.
- 😀 Bernoulli's equation is used to derive the velocity of a fluid in the pipe based on the differences in pressure and fluid height at different points.
- 😀 Key points for velocity measurement in a Pitot tube include the stagnation point where the fluid comes to rest, and the pressure difference between points 2 and 3.
- 😀 The script discusses the simplifications and assumptions made in fluid dynamics, such as assuming certain heights and pressures are equal at different points.
- 😀 The equation for the velocity of the fluid in the pipe is derived using Bernoulli’s equation and hydrostatic pressure principles.
- 😀 A correction factor (cp-cv) is applied to the calculated velocity to account for real-world conditions based on calibration.
- 😀 The script explains how to calculate the flow rate (debit) of the fluid using the velocity and surface area of the pipe, integrating over the area.
- 😀 The mass flow rate can be calculated by multiplying the velocity by the fluid density, helping to determine the volumetric flow.
- 😀 The importance of understanding and using correction factors in real-world applications is emphasized to ensure accurate measurement and flow calculations.
Q & A
What is the main topic of the video?
-The video discusses the Pitot tube, explaining how it works to measure fluid velocity using Bernoulli's principle and hydrostatic equations.
What are the key components discussed in relation to the Pitot tube?
-The video highlights several key components, including the fluid flow, manometer (which may contain mercury or another fluid), and specific points of measurement (such as points 1, 2, and 3 on the diagram).
How is velocity calculated using the Pitot tube in the video?
-Velocity is calculated using Bernoulli's equation and the hydrostatic principles, where the difference in fluid height in the manometer is used to derive the fluid velocity.
What are the assumptions made in the calculations of the Pitot tube's velocity?
-Assumptions include that the points of measurement (like points 2 and 3) are at the same height and that certain terms, like pressure and fluid height at specific points, can be approximated for simplicity.
What is the significance of the stagnation point mentioned in the video?
-The stagnation point is where the fluid velocity becomes zero. It is a key concept for determining the pressure difference in the Pitot tube, allowing for the calculation of velocity.
What does the correction factor (Cp-Cv) refer to in the context of the Pitot tube?
-The correction factor (Cp-Cv) is used to account for real-world conditions that may differ from ideal assumptions. It is a factor that adjusts the velocity calculation for better accuracy.
How is the velocity equation simplified in the video?
-The equation is simplified by eliminating terms that are assumed to be zero or constant, such as the potential energy terms at points of the same height, resulting in an equation that calculates velocity based on the pressure difference.
How does the video explain the relationship between pressure and fluid velocity?
-The video explains that the difference in fluid pressure at various points, measured by the manometer, is directly related to the velocity of the fluid, using Bernoulli's equation to connect pressure, velocity, and fluid density.
What role does the manometer play in the Pitot tube measurement process?
-The manometer is used to measure the pressure difference at different points in the fluid flow. The difference in height between the mercury levels in the manometer corresponds to the pressure difference, which is then used to calculate fluid velocity.
What is the significance of integrating the velocity function to calculate flow rate?
-The integration of the velocity function allows for the calculation of the flow rate (Q), taking into account the varying velocity across the cross-section of the pipe. The integral helps determine the total volume of fluid flowing through the pipe.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Fluida Dinamis - Konsep Bernoulli - Simple Konsep - Fisika Kelas 11
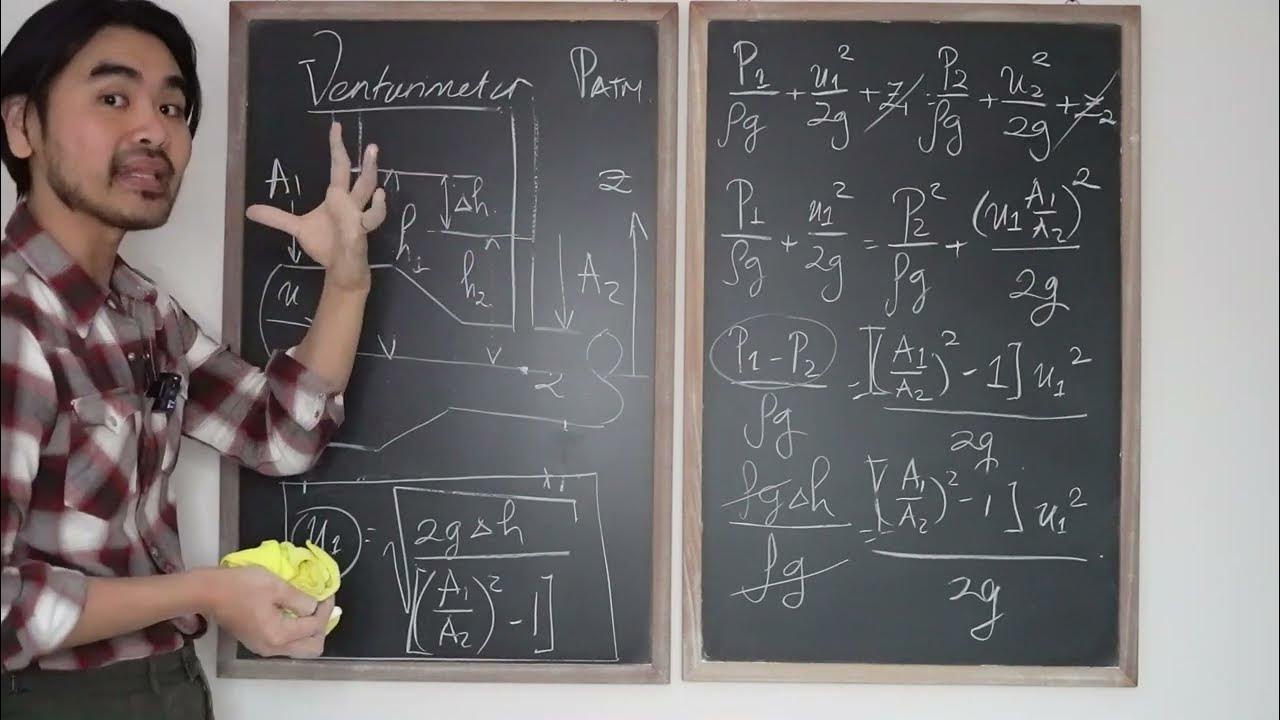
Mekanika Fluida FM01 (Lecture3: 6/8). Venturimeter - Aplikasi persamaan Bernoulli
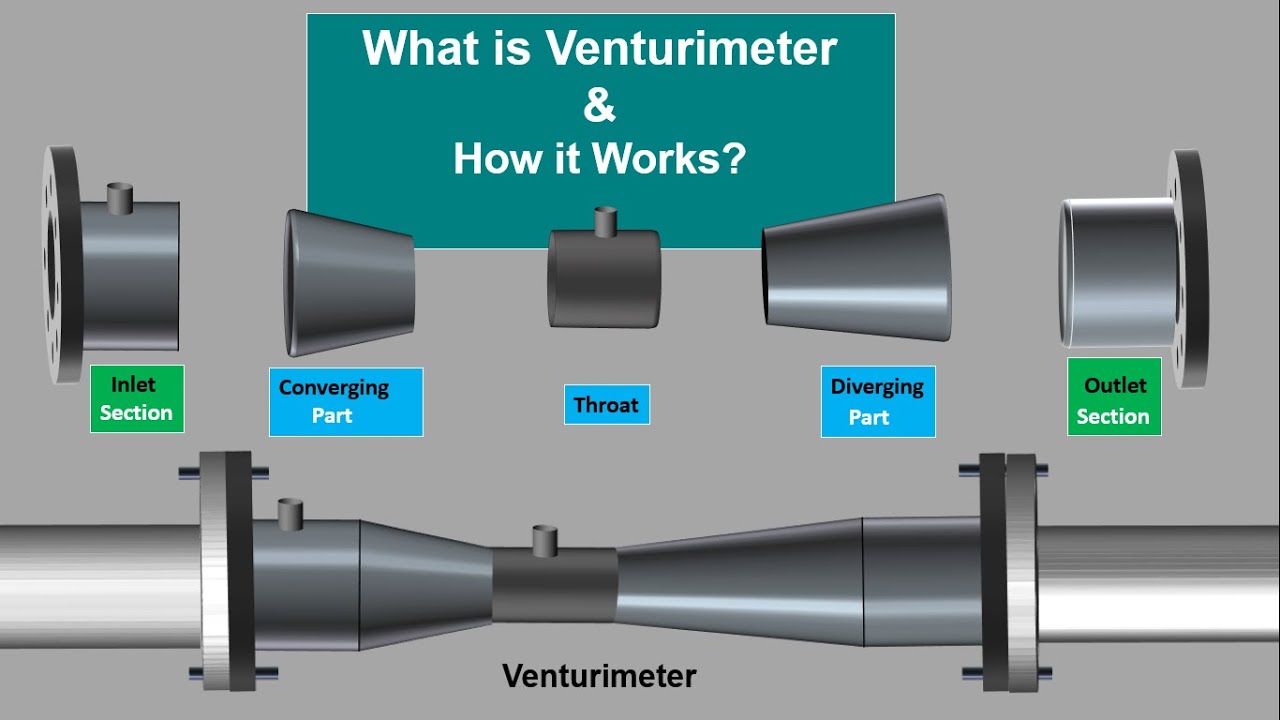
What is Venturimeter. How Venturimeter works. Working Principle of Venturimeter.Animation Video.

Dinamika Fluida

Rotameter Working Explanation with 3d Animation

Fluida Dinamis • Part 3: Gaya Angkat Sayap Pesawat dan Tabung Pitot
5.0 / 5 (0 votes)
