El PÉNDULO SIMPLE NO es como te explicaron | Física y Matemáticas
Summary
TLDREn este video se explora el movimiento de un péndulo simple desde una perspectiva matemática. Se introducen las variables clave y se aplican las leyes de Newton para derivar una ecuación diferencial que describe el movimiento del péndulo. Se compara el periodo de oscilación utilizando fórmulas para ángulos pequeños y grandes, destacando la inadecuación de la fórmula común para ángulos mayores. Además, se incorpora el efecto del rozamiento con el aire, mostrando cómo afecta la altura del péndulo con el tiempo. El video finaliza con una invitación a explorar el péndulo doble en el próximo episodio.
Takeaways
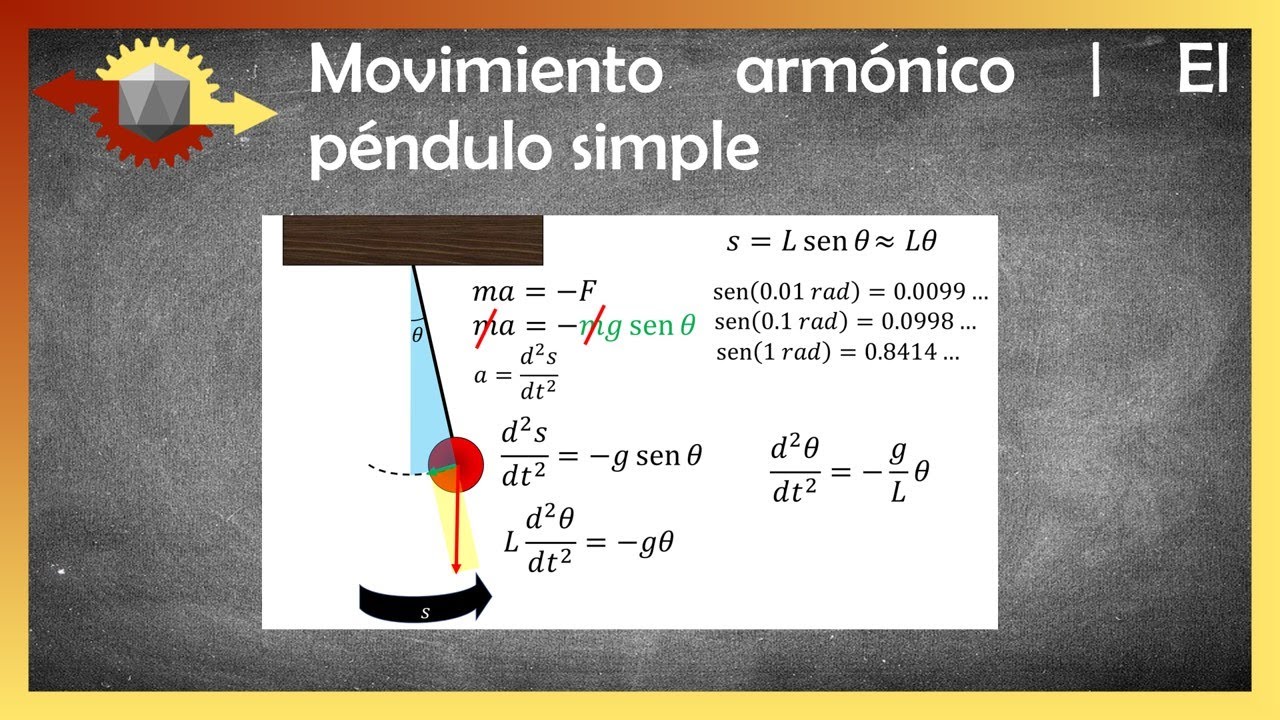
- 😀 El péndulo simple es un sistema que oscila bajo la influencia de la gravedad, y su movimiento puede ser modelado matemáticamente.
- 🔍 Se debe considerar el ángulo z y la longitud de la cuerda al estudiar el movimiento del péndulo.
- 📉 Para ángulos pequeños, el movimiento del péndulo se puede aproximar a funciones trigonométricas como el seno y el coseno.
- 📊 Al aumentar el ángulo inicial, la aproximación a funciones trigonométricas se vuelve menos precisa.
- 📜 La ecuación que describe el movimiento del péndulo es una ecuación diferencial de segundo orden.
- 🔗 Al suponer que el péndulo no tiene rozamiento, la masa del péndulo no afecta su movimiento, ya que las masas se cancelan en la ecuación.
- ⏳ El periodo del péndulo se calcula con una fórmula que varía según el ángulo inicial, siendo la aproximación válida solo para pequeños ángulos.
- 🔧 La fórmula del periodo para oscilaciones grandes se obtiene a través de funciones elípticas, lo que la hace más compleja.
- 🌬️ Al introducir el rozamiento del aire, se añade un término a la ecuación, lo que reduce la altura alcanzada en cada oscilación.
- 🔮 El próximo video explorará el péndulo doble, un sistema más complejo que genera movimiento caótico.
Q & A
¿Qué es un péndulo simple y cómo se comporta bajo la gravedad?
-Un péndulo simple es un sistema físico que consiste en una masa suspendida de un punto fijo por una cuerda rígida. Bajo la influencia de la gravedad, al soltarlo, oscila de un lado a otro, moviéndose hacia la misma altura en posiciones simétricas.
¿Cuáles son las variables definidas para analizar el péndulo?
-Se definen tres variables: m para la masa del péndulo, l para la longitud de la cuerda y z para el ángulo que forma la cuerda con la vertical.
¿Qué suposiciones se hacen para simplificar el problema del péndulo?
-Se asume que la cuerda no tiene masa, que la masa es puntual y que no hay rozamiento con el aire.
¿Cómo se relaciona el movimiento del péndulo con funciones trigonométricas?
-El movimiento del péndulo, al graficar el ángulo z en función del tiempo, se asemeja a una función trigonométrica como el coseno, especialmente para ángulos pequeños.
¿Por qué el péndulo no siempre se comporta como una función trigonométrica?
-Para ángulos más grandes, la forma del movimiento se aleja de las funciones trigonométricas debido a la no linealidad de la ecuación que describe su movimiento.
¿Qué es la segunda ley de Newton y cómo se aplica al péndulo?
-La segunda ley de Newton establece que el sumatorio de fuerzas sobre un objeto es igual a su masa por la aceleración. Se aplica al péndulo al analizar las fuerzas que actúan sobre la masa y determinar su movimiento.
¿Cuál es la diferencia entre las soluciones de la ecuación original y la aproximación para pequeños ángulos?
-Las soluciones para la ecuación original (naranja) y la aproximación (azul) son similares para ángulos pequeños, pero divergen a medida que aumenta el ángulo inicial, con la aproximación volviéndose menos precisa.
¿Qué fórmula se utiliza para calcular el período del péndulo y qué limitaciones tiene?
-La fórmula del período del péndulo para oscilaciones pequeñas es T = 2π√(l/g), pero no considera el ángulo inicial, lo que la hace inapropiada para ángulos mayores.
¿Cómo se introduce el rozamiento en el modelo del péndulo y qué efecto tiene?
-Se introduce un término adicional en la ecuación que depende de la velocidad del péndulo, lo que genera una resistencia que amortigua el movimiento y hace que el péndulo no alcance la misma altura en oscilaciones sucesivas.
¿Qué se anticipa en el próximo video relacionado con el péndulo?
-Se anticipa la exploración de un péndulo doble, que es un sistema más complejo y que puede exhibir comportamientos caóticos.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)