Intro to FOURIER SERIES: The Big Idea
Summary
TLDRIn this video, the speaker explores Fourier series, a powerful mathematical tool with wide-ranging applications in physics and engineering. They begin by explaining periodic functions, using sine as a primary example, and demonstrate how sine can approximate a square wave. By adding multiple sine terms, the approximation improves, showcasing the essence of Fourier series as sums of trigonometric terms. Key concepts like the Gibbs phenomenon, which highlights overshooting at discontinuities, are introduced. The video promises further exploration of calculating Fourier coefficients and their relevance to differential equations, inviting viewers to engage through likes and comments.
Takeaways
- 🎓 Fourier series are powerful mathematical tools with applications in differential equations, physics, and engineering.
- 🔄 A periodic function repeats its values at regular intervals; sine and cosine functions are quintessential examples.
- 📏 The period of a function, such as sine, is defined as the distance over which the function repeats, e.g., 2π for sine.
- 🔊 A square wave is an example of a periodic function that oscillates between values of 1 and -1.
- ⚙️ The approximation of complex periodic functions can be improved by adding sine terms of varying frequencies.
- 📈 Adding multiple sine terms together can create a continuous approximation of a discontinuous function, such as a square wave.
- ✨ The Fourier series concept involves summing trigonometric functions to represent periodic functions more accurately.
- 📊 The Gibbs phenomenon refers to overshooting at discontinuities in the approximation of a function using Fourier series.
- 📏 Fourier series can be expressed as a combination of constant, cosine, and sine terms with specific coefficients.
- 🔍 Future videos will address how to find Fourier coefficients and explore the convergence of Fourier series in different contexts.
Q & A
What is the main focus of the video?
-The video focuses on introducing Fourier series, explaining its significance in mathematics, and its applications in various fields like differential equations, physics, and engineering.
What is a periodic function?
-A periodic function is a function that repeats its values at regular intervals, defined by a period. For example, the sine function is 2π-periodic, meaning it returns to the same height every 2π units.
How does the video demonstrate the concept of Fourier series?
-The video illustrates Fourier series by showing how to approximate a square wave using a sum of sine functions with varying frequencies, highlighting how more terms lead to better approximations.
What is the significance of sine and cosine terms in Fourier series?
-Sine and cosine terms are used in Fourier series to approximate periodic functions because they are themselves periodic and can represent various frequencies and amplitudes needed to match the target function.
What is the Gibbs phenomenon?
-The Gibbs phenomenon refers to the overshooting that occurs at the discontinuities of a function when approximated by Fourier series. It results in an overshoot in the approximation near the points of discontinuity.
What are the coefficients a₀, aₙ, and bₙ in Fourier series?
-In Fourier series, a₀ represents the average value of the function over one period, while aₙ and bₙ are coefficients that determine the contribution of cosine and sine terms, respectively, to the series.
How can you find the coefficients aₙ and bₙ?
-The coefficients aₙ and bₙ can be calculated using specific integrals over the function's period, which capture how much of each sine and cosine term is present in the original function.
What types of functions can be approximated by Fourier series?
-Fourier series can approximate a wide variety of periodic functions, including piecewise continuous functions. However, the convergence behavior depends on the characteristics of the function.
What connection does Fourier series have with differential equations?
-Fourier series are often used in solving differential equations, especially in contexts involving periodic boundary conditions, as they allow for the decomposition of functions into simpler trigonometric components.
What will be covered in the upcoming videos following this one?
-The upcoming videos will address how to calculate the coefficients of Fourier series, the conditions for convergence, and the applications of Fourier series in solving differential equations.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

What is the Fourier Transform used for?

Transform Calculus and its applications in Differential Equations

What is Continuous Wavelet Transform (CWT)? | Wavelet Theory | Advanced Digital Signal Processing

FOURIER SERIES LECTURE 1 | STUDY OF DEFINITION AND ALL BASIC POINTS @TIKLESACADEMY

MATERI MATEMATIKA YANG WAJIB DIKUASAI UNTUK MENGERJAKAN SOAL-SOAL OSN FISIKA SMA
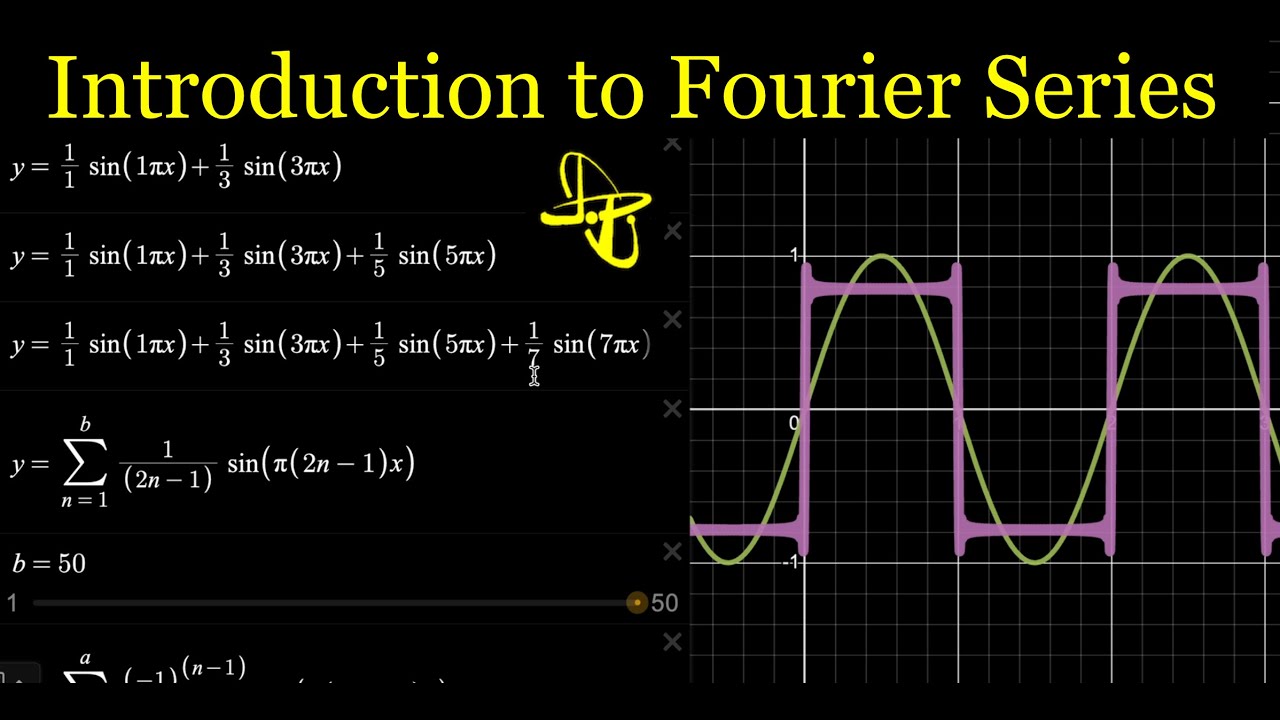
Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves
5.0 / 5 (0 votes)
