35. Ley de Gauss- Ejercicio basico para comprender
Summary
TLDREl vídeo aborda la resolución de un ejercicio de ley de Gauss, calculando la carga de un conductor esférico aislado y el campo eléctrico a 0.5 metros de su centro. Se utiliza la distribución de carga uniforme y se aplican los principios de la ley de Gauss para calcular la carga neta y el campo eléctrico. El proceso incluye el desarrollo de ecuaciones y el análisis del campo eléctrico en puntos específicos. Es una guía didáctica sobre la aplicación de la ley de Gauss en problemas de física eléctrica.
Takeaways
- 📚 El video forma parte de un curso sobre la ley de Coulomb y el campo eléctrico.
- 🌐 Se resuelve un ejercicio aplicando la ley de Gauss a un conductor esférico de radio 0.16 metros con distribución de carga uniforme.
- 🔋 El campo eléctrico a una distancia mínima fuera de la superficie del conductor es de 1.151 Newtons sobre Coulomb.
- 🧮 Se utiliza la ley de Gauss para calcular la carga neta del conductor, que resulta en 3.276 x 10^-9 Coulombs.
- 📈 Seguidamente, se calcula el campo eléctrico a una distancia de 0.5 metros del centro del conductor.
- 📐 Se traza una superficie de Gauss imaginaria para aplicar la ley de Gauss, en este caso, una esfera con un radio de 0.5 metros.
- ⚖️ La carga neta es despejada usando la ley de Gauss, y se relaciona con el campo eléctrico y el radio de la superficie de Gauss.
- 🔬 El ángulo entre el vector campo eléctrico y el vector de superficie de Gauss es de 0 grados, ya que ambos son paralelos.
- 🧲 El campo eléctrico en el punto calculado es de 117.775 Newtons por Coulomb, y su dirección es hacia afuera de la superficie de la esfera.
- 📸 Se recomienda suscribirse y seguir en redes sociales para recibir notificaciones de nuevos contenidos.
- 📚 El video incluye un enlace a un video anterior que explica en detalle la ley de Gauss y su importancia en la física.
Q & A
¿Qué es la ley de Gauss y cómo se aplica en el ejercicio?
-La ley de Gauss es una herramienta fundamental en electrostática que relaciona el flujo eléctrico a través de una superficie cerrada con la carga eléctrica encerrada dentro de esta superficie. En el ejercicio, se utiliza para calcular la carga neta de un conductor esférico usando el valor del campo eléctrico justo fuera de su superficie.
¿Cuál es el valor del campo eléctrico dado en el problema y qué representa?
-El valor del campo eléctrico dado es de 1.150 newtons por coulomb. Este valor representa la intensidad del campo eléctrico justo fuera de la superficie del conductor esférico.
¿Cómo se calcula la carga neta del conductor utilizando la ley de Gauss?
-Para calcular la carga neta usando la ley de Gauss, se multiplica el campo eléctrico por el área superficial de la superficie gaussiana (que en este caso es esférica y coincide con el conductor) y por la constante 4π. Esto relaciona directamente el flujo eléctrico total con la carga neta encerrada.
¿Qué es una superficie gaussiana y cómo se selecciona en este ejercicio?
-Una superficie gaussiana es una superficie cerrada imaginaria utilizada para aplicar la ley de Gauss. En este ejercicio, la superficie gaussiana es una esfera que coincide exactamente con la superficie del conductor esférico, facilitando los cálculos debido a la simetría de la situación.
¿Por qué es importante que el campo eléctrico tenga el mismo valor en todos los puntos de la superficie gaussiana?
-Es importante porque permite simplificar la integral en la ley de Gauss. Al ser constante, el campo eléctrico puede salir de la integral de superficie, y la integral se reduce a calcular el área de la superficie gaussiana.
¿Cómo se calcula el campo eléctrico a una distancia de 0.5 metros del centro del conductor?
-Se utiliza de nuevo la ley de Gauss con una superficie gaussiana esférica de radio 0.5 metros. El campo eléctrico se calcula dividiendo la carga neta por el producto de 4π, el cuadrado del radio de la nueva superficie gaussiana y la permitividad del vacío.
¿Qué significa que el vector de campo eléctrico y el vector área sean paralelos en este contexto?
-Significa que el ángulo entre el vector de campo eléctrico y el vector normal a la superficie (vector área) es cero grados, lo que implica que el coseno de este ángulo es 1. Esto simplifica el cálculo del producto escalar en la integral de la ley de Gauss.
¿Qué implica el resultado obtenido para la magnitud del campo eléctrico a 0.5 metros del centro?
-El resultado obtenido indica que la intensidad del campo eléctrico disminuye con la distancia desde el centro del conductor, siguiendo la ley del inverso del cuadrado, lo cual es típico para campos creados por cargas puntuales o distribuciones esféricas simétricas de carga.
¿Cuál es el propósito de mencionar el seguimiento en redes sociales al final del vídeo?
-El propósito es aumentar la interacción y el compromiso del público con el contenido del canal. Invitar a los espectadores a suscribirse y seguir en redes sociales ayuda a construir una comunidad activa y fomenta la difusión del material educativo.
¿Qué rol juega la permitividad del vacío en los cálculos del campo eléctrico?
-La permitividad del vacío es una constante que aparece en las ecuaciones de la ley de Gauss y en la ley de Coulomb para calcular campos eléctricos. Modifica la relación entre la carga y el campo eléctrico, siendo fundamental para obtener medidas precisas en unidades del Sistema Internacional.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

44. Campo eléctrico generado por un hilo cargado infinito- Ley de Gauss
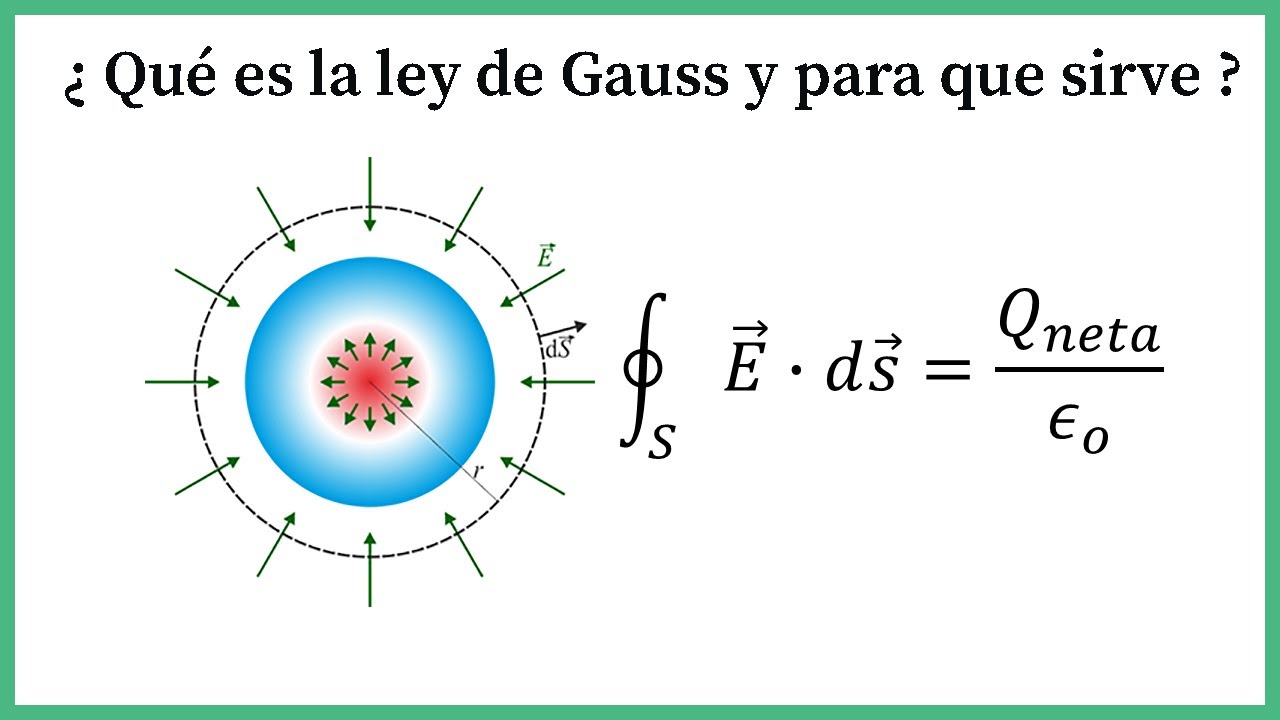
34. Ley de Gauss Explicación-Todo lo que debes saber

CAMPO ELÉCTRICO ¡Una fuerza invisible que nos rodea!

Universo Mecánico 29 El Campo Eléctrico

Física: Ley de Gauss - Traful

Gauss's Law and Applications | 3D Animation Explained | 12th physics | Electrostatics
5.0 / 5 (0 votes)
