Lecture: Model-based control design

Summary

In this lecture on model-based control design, the speaker explains how to derive ideal controllers from process models, focusing on set point responses and disturbance rejection. Key concepts such as closed-loop transfer functions and various controller types—PI, PID, proportional, and proportional-derivative—are explored through examples of first-order, second-order, and integrating systems. The lecture emphasizes the importance of tuning parameters and disturbance rejection, illustrating the practical applications of these control strategies in engineering. Overall, the session provides valuable insights into achieving effective and responsive control system design.

Takeaways

• 😀 Model-based control design focuses on finding an ideal controller for a given process model.
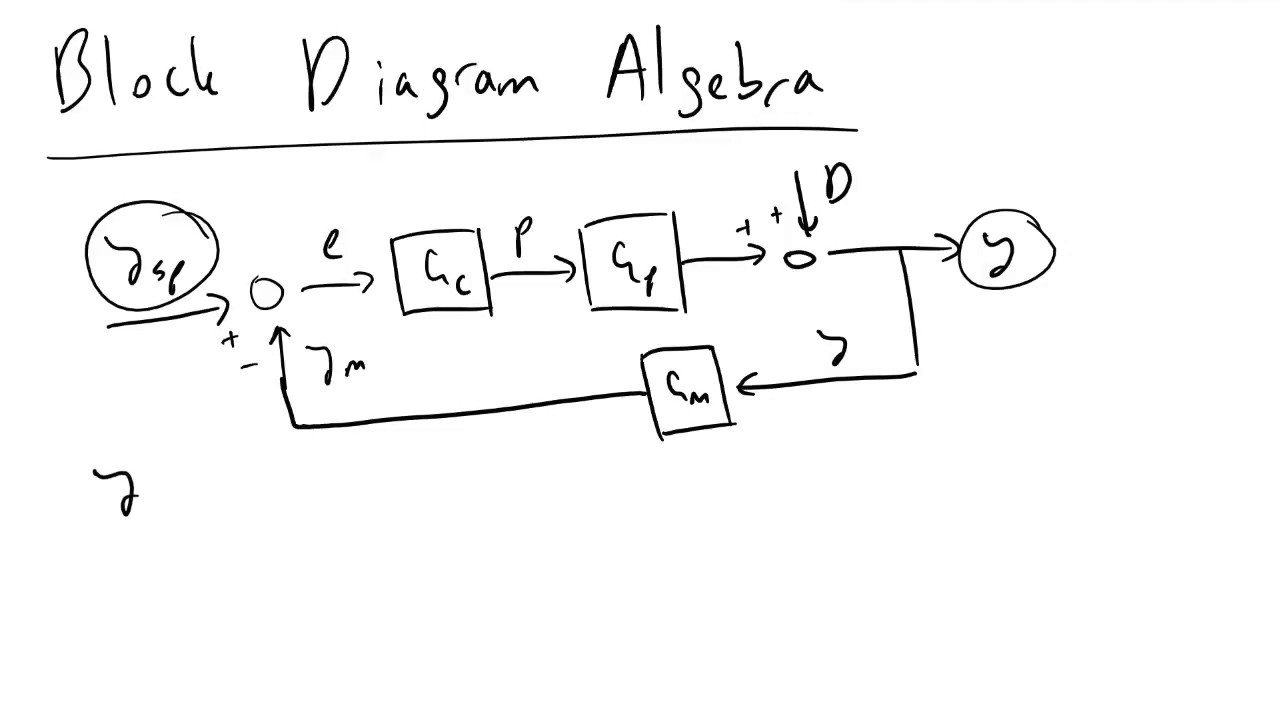
• 📊 The closed-loop transfer function is defined as CG divided by 1 plus GC, allowing for the analysis of system response.
• 🔄 The desired closed-loop response is specified, leading to a solution for the associated controller.
• ⚙️ A first-order system can be represented with a simple transfer function, aiding in determining control parameters.
• ⏱ The closed-loop time constant (tau C) is crucial for defining the speed of the feedback controller response.
• 🧩 For a first-order system, the optimal controller is a PI controller, with tuning rules derived for parameters KC and tau I.
• 🔍 For second-order systems, the optimal controller is a PID controller, which also follows specific tuning rules.
• 📈 In integrating systems, the optimal controller simplifies to a proportional controller, as the system integrates the input.
• 🛠 Servo systems may use a proportional-derivative controller, particularly in applications like robotics and conveyor belts.
• 🔄 Disturbance rejection is a key function of controllers, highlighting their role in maintaining system stability despite external changes.

Q & A

What is the main focus of the lecture?

The lecture focuses on model-based control design, specifically how to find an associated controller given a process model.

What does the term 'closed-loop transfer function' refer to?

The closed-loop transfer function describes the relationship between the output and the input of a system when feedback is applied, and it can be calculated using the formula Y = GC / (1 + GC) times the set point.

How is the desired closed-loop response determined?

The desired closed-loop response is specified by setting the closed-loop transfer function equal to an arbitrary transfer function T, which represents the desired behavior of the system.

What is the significance of the time constant tau_C?

The time constant tau_C is a tuning parameter that determines how quickly the feedback controller responds to changes in the set point; a smaller tau_C results in a faster response.

What type of controller is optimal for a first-order system?

For a first-order system, the optimal controller is a Proportional-Integral (PI) controller, which can be derived from the formula C = 1/(G * T(1 - T)).

How are the tuning parameters KC and tau_I calculated for a first-order system?

The tuning parameters are calculated as KC = 1/(K * tau_C) and tau_I = tau, where K is the process gain and tau is the process time constant.

What distinguishes a second-order system from a first-order system in terms of control?

A second-order system typically requires a Proportional-Integral-Derivative (PID) controller for optimal control, which incorporates proportional, integral, and derivative terms to handle more complex dynamics.

What is the role of disturbance rejection in control systems?

Disturbance rejection is crucial for maintaining the stability and performance of a control system; it allows the system to handle unexpected changes in input without significantly deviating from the set point.

How does feed-forward control complement feedback control?

Feed-forward control helps to mitigate disturbances by adjusting the control action based on the expected impact of disturbances, allowing for a more proactive response compared to feedback control alone.

Why is it important to understand the dynamics of disturbances in a control system?

Understanding the dynamics of disturbances is important because it helps in designing controllers that can effectively counteract disturbances and maintain system performance.