SA21: Virtual Work Method (Trusses)
Summary
TLDRThe video discusses the Method of Virtual Work in structural analysis, emphasizing its application to calculate displacements in beams and trusses. It builds on the Work Energy principle, illustrating how external work correlates with internal energy changes. Key equations are presented to demonstrate this relationship, alongside a practical example analyzing a truss structure under load. The method allows for calculating displacements at any point by introducing virtual loads, thereby simplifying complex structural analyses. The tutorial showcases the effectiveness of the virtual work method, providing engineers with a vital tool for understanding and designing safe structures.
Takeaways
- 📐 The Method of Virtual Work is an extension of the Work Energy principle, enabling the calculation of displacements in structures.
- 📏 For simply supported beams, the work-energy equation relates external work done by loads to internal energy stored in the beam.
- 🛠️ The equation for a simply supported beam can be expressed as: 1/2 P Δ = 1/2 ∫ M dθ, where P is the load, Δ is the displacement, M is the bending moment, and θ is the slope of the elastic curve.
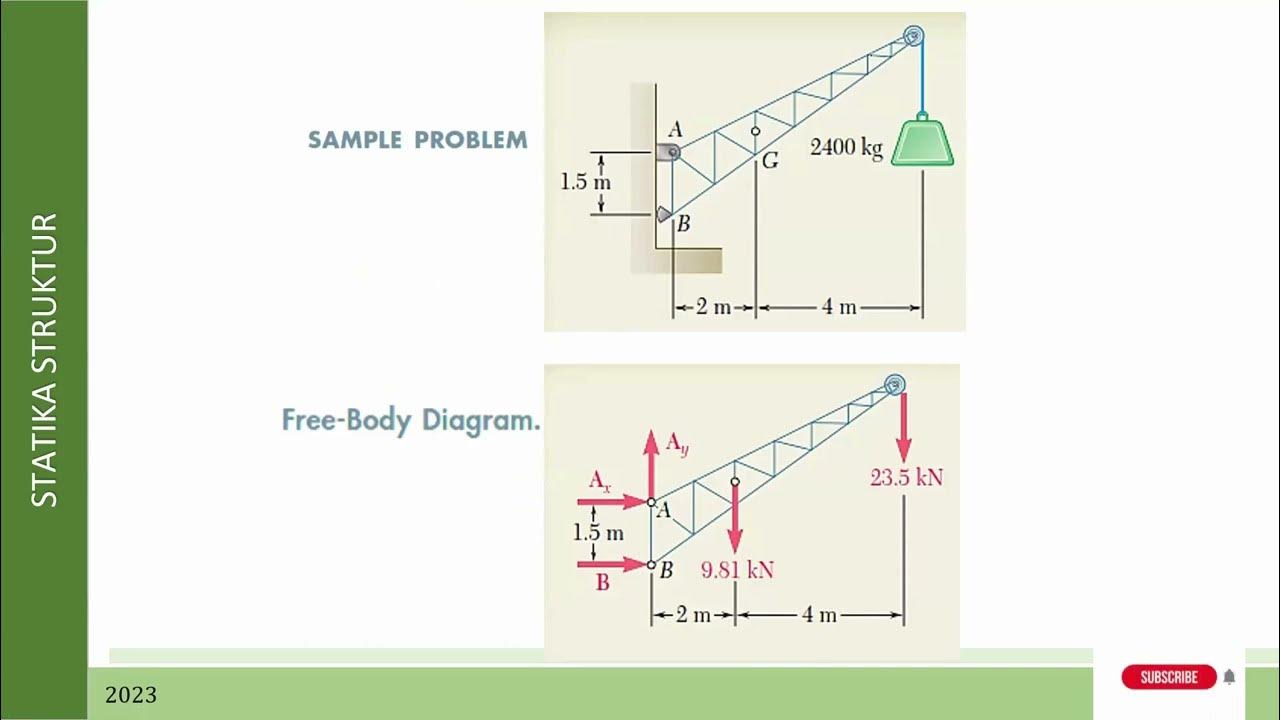
- 🏗️ The Method of Virtual Work can also be applied to trusses, allowing for the calculation of displacements at arbitrary points.
- 🧮 A virtual load can be introduced to analyze member forces and compute virtual work, facilitating displacement calculations.
- ⚖️ The principle of virtual work states that external virtual work equals internal virtual work, represented by P* ΔV = Σ f*_i δ_i.
- 🔧 Virtual loads are imaginary and can be assigned any value to simplify calculations, often chosen as unit loads.
- 📈 Member elongation due to real loads can be determined using Hooke's Law, relating axial stress, strain, and elongation.
- 📊 For example, using the equation (FL)/(EA), the elongation of each truss member can be calculated based on its force, length, modulus of elasticity, and cross-sectional area.
- 📏 The calculated displacements at points C, B, and D provide insight into how the truss structure deforms under applied loads, demonstrating the effectiveness of the virtual work method.
Q & A
What is the Method of Virtual Work?
-The Method of Virtual Work is a technique used in structural analysis to calculate displacements at any point in a structure by equating external virtual work done by imaginary loads to internal virtual work due to real loads.
How does the Work Energy Principle relate to the Method of Virtual Work?
-The Work Energy Principle relates external work done on a structure to the internal energy stored within it. The Method of Virtual Work builds on this principle by using imaginary loads to simplify the calculation of displacements.
What is the equation for a simply supported beam under a concentrated load?
-For a simply supported beam subjected to a concentrated load, the work energy equation can be written as: 1/2 P Δ = 1/2 ∫ M dθ, where P is the load, Δ is the displacement, M is the bending moment, and θ is the slope of the elastic curve.
How can you calculate horizontal displacement at a truss joint?
-To calculate horizontal displacement at a truss joint, you place a unit virtual load in the horizontal direction at that joint and calculate the resulting member forces, using the equation: Δ = ∑ f*i δ_i, where f*i is the virtual force in member i and δ_i is the elongation due to real loads.
What are the steps to determine vertical displacement at point B?
-To determine vertical displacement at point B, you place a unit virtual load in the vertical direction at B, calculate the member forces due to this load, and then apply the internal virtual work equation to find the vertical displacement.
What does it mean if the axial elongation of a member is negative?
-If the axial elongation of a member is negative, it indicates that the member is experiencing compression, meaning it is shortening rather than elongating.
What is the significance of using a unit virtual load in the Method of Virtual Work?
-Using a unit virtual load simplifies calculations by allowing engineers to directly relate the virtual work done to the actual displacements, making it easier to solve for unknown displacements.
How is axial elongation calculated according to Hooke's Law?
-Axial elongation is calculated using the formula: δ = (F * L) / (E * A), where F is the axial force, L is the original length of the member, E is the modulus of elasticity, and A is the cross-sectional area.
What are the internal virtual work expressions for truss members?
-The internal virtual work for truss members is expressed as: W_internal = ∑ f*i δ_i, where f*i is the virtual force due to the virtual load and δ_i is the real elongation due to actual loads.
What were the calculated displacements for the example truss structure presented?
-For the example truss structure, the calculated displacements were: horizontal displacement at C = 0.02 mm, vertical displacement at B = 0.00967 mm, and horizontal displacement at D = 0.008 mm.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

SA22: Virtual Work Method (Beams)

SA20: Work-Energy Principle (Part 2)

ANALISA STRUKTUR 2 KONSEP DASAR MATRIKS FLEKSIBILITAS#flexibilitymatrix#Flexibility#matrix

S-10 Pengenalan Truss

Mekanika Statis Tentu: Struktur dan Elemen Bangunan
Teori Dasar Struktur Truss: Persamaan/Rumus, Reaksi Tumpuan, Gaya tarik atau tekan (T atau C)
5.0 / 5 (0 votes)
