SA22: Virtual Work Method (Beams)

Summary

This lecture introduces the Virtual Work Method for calculating deflections and slopes in beams and trusses. It explains how to apply virtual loads at specific joints or points to compute displacements and bending moments, utilizing the principle that external virtual work equals internal virtual work. Through clear examples, including simple beams and cantilever beams under distributed loads, the method is demonstrated in calculating vertical deflection and slope at key locations. The lecture emphasizes the utility of this technique in structural analysis, laying the foundation for further exploration in frame analysis in future lessons.

Takeaways

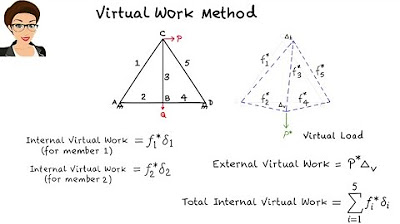
• 😀 The Virtual Work Method calculates joint displacement in trusses and deflection/slope in beams by equating external and internal virtual work.
• 😀 For trusses, the direction of the virtual load should match the desired displacement direction (horizontal or vertical).
• 😀 External virtual work is calculated as the product of the virtual load and displacement (p* × Δ).
• 😀 Internal virtual work involves summing the forces in each truss member and their corresponding elongations under real load.
• 😀 In beams, bending moments are the primary internal forces contributing to deflection, and the method focuses on these forces for displacement calculations.
• 😀 The displacement at a specific point on a beam (e.g., mid-span) can be found by placing a virtual unit load and integrating the corresponding bending moments over the beam's length.
• 😀 The bending moment equation for a beam is essential for calculating deflections using the Virtual Work Method.
• 😀 The relationship between the bending moment (M) and radius of curvature (ρ) is key to determining internal deformation in beams due to bending.
• 😀 For beam deflection calculations, integrating the product of the virtual moment and the moment due to the real load gives the displacement at the desired location.
• 😀 The Virtual Work Method can also be used to calculate the slope at any point on a beam, such as at the cantilever's end, by applying a virtual moment rather than a load.
• 😀 The method is highly flexible and can be extended to complex structures like frames, which will be covered in future lessons.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.