Big-O notation in 5 minutes

Summary

In this video, you'll learn about Big O notation, a method for analyzing the efficiency of algorithms in terms of input size (n). Big O helps abstract the complexity of algorithms by focusing on their fundamental computer steps rather than machine specifics. The video covers common time complexities like constant time (O(1)), linear time (O(n)), and quadratic time (O(n²)), emphasizing worst-case scenarios and ignoring constants. Through examples, you'll understand how to analyze code blocks and loops. The video concludes by noting that in real-world coding, constants and input size often do matter.

Takeaways

• 🧠 Big O notation is used to analyze the efficiency of algorithms, particularly in terms of input size (n).
• 📊 It helps abstract the efficiency of code, ignoring the specifics of the machine it runs on.
• ⏳ Big O can be used to analyze both time and space complexity of algorithms.
• ⚖️ When discussing Big O, worst-case scenario is typically the focus, though best-case and average-case are also important.
• 🚫 Constants are ignored in Big O notation; for example, a running time of 5n is simplified to O(n).
• 📉 Lower-order terms are dropped when dominated by higher-order ones as n grows large.
• 💻 Constant time operations (O(1)) do not depend on the size of the input.
• 🔄 Linear time (O(n)) occurs when an operation is repeated n times, such as in a for loop.
• 🔢 Quadratic time (O(n²)) arises when operations are repeated in a nested manner, like a loop inside another loop.
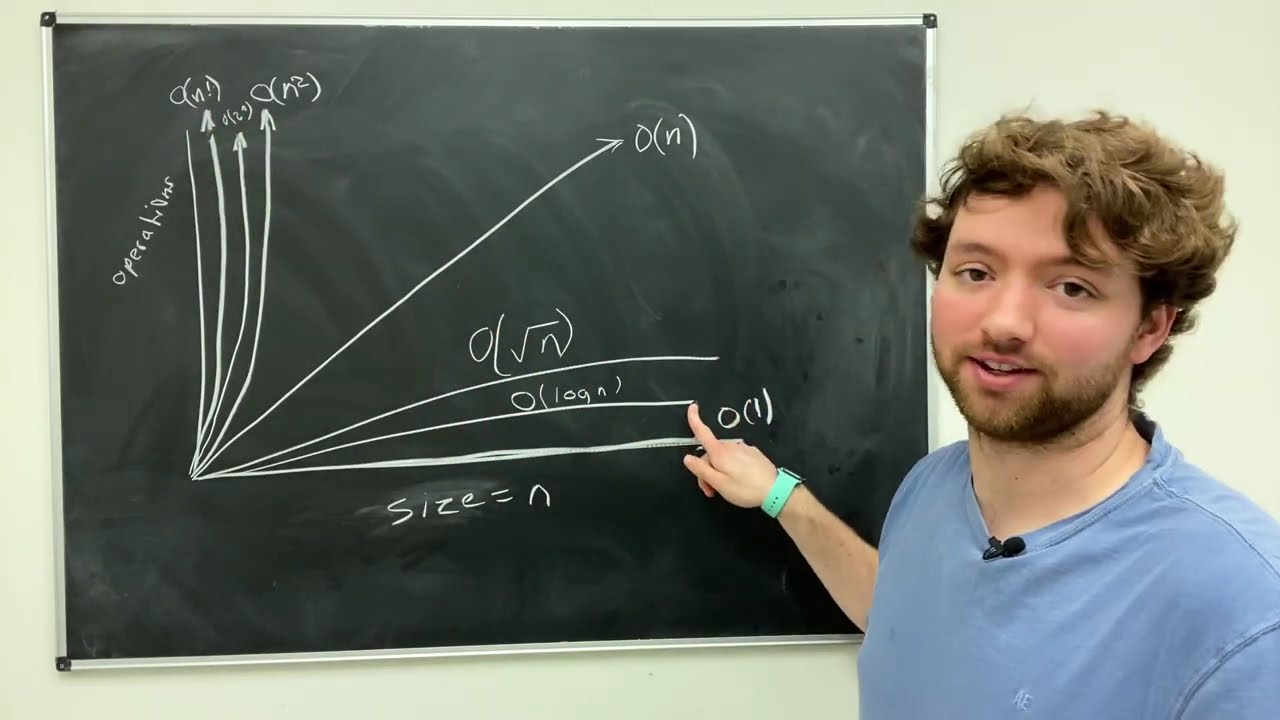
• 🔍 When analyzing total runtime, the dominating factor is chosen; for example, O(n²) dominates O(n).

Q & A

What is Big O notation?

Big O notation is a way to simplify the analysis of an algorithm's efficiency. It helps us understand how long an algorithm will take to run based on the size of the input.

Why do we use Big O notation?

We use Big O notation to abstract the efficiency of algorithms from the specific machines they run on. This allows us to compare algorithms and focus on their performance in terms of time and space.

What does Big O notation typically measure?

Big O notation measures an algorithm's complexity in terms of time and space relative to the input size, denoted as 'n'. It helps evaluate how an algorithm performs as the input size grows.

When analyzing algorithms with Big O, which case do we typically focus on?

When using Big O notation, we typically focus on the worst-case scenario to ensure the algorithm's performance is acceptable under the most demanding conditions.

Why does Big O notation ignore constants in expressions like 5n?

Big O ignores constants because, as the input size 'n' grows large, the constant factors (like 5) become less significant in comparison to the overall growth rate of the function.

How do we handle low-order terms in Big O notation?

In Big O notation, low-order terms are dropped when they are dominated by higher-order terms as the input size grows. For example, in a function like n^2 + n, we only consider n^2.

What is the Big O of a function that runs in constant time?

A function that runs in constant time, meaning its execution does not depend on the input size, has a Big O of O(1).

How do we calculate the Big O for a block of constant time statements?

If we have multiple constant time statements, their Big O values are summed up. However, since Big O notation ignores constants, the overall complexity remains O(1).

What is the Big O of a for loop that runs n times?

A for loop that runs n times has a time complexity of O(n), as each iteration involves a constant time operation, repeated n times.

What is the time complexity of a nested loop?

A nested loop, where each loop runs 'n' times, results in a time complexity of O(n^2), as the inner loop runs n times for each iteration of the outer loop.

How do we determine the Big O of code with multiple components?

When calculating Big O for code with multiple components, we choose the part of the code with the largest time complexity. For example, in code with O(n) and O(n^2) components, the total complexity is O(n^2).

How should constants be considered in real-world algorithm performance?

In real-world coding, constants do matter, especially with small input sizes. A constant factor of 2 or 3 could significantly impact the performance of an algorithm.

Why should you consider best and average cases in addition to the worst-case scenario?

Depending on the application, best and average cases may be more relevant for assessing an algorithm's performance, especially if the worst-case scenario is rare.