Y1 3) Index Numbers
Summary
TLDRThis video explains the importance and use of index numbers in economics. Index numbers simplify complex and large figures, making data like GDP, house prices, or inflation easier to analyze and compare. The video demonstrates how to convert raw numbers into index numbers by selecting a base year and applying a simple formula. Additionally, it highlights how index numbers facilitate the calculation of percentage changes and rates of growth, allowing for quick and easy comparisons between different time periods. This method simplifies otherwise difficult-to-handle economic data.
Takeaways
- 📊 Index numbers are frequently used in economics for various data sets, including GDP, house prices, and inflation.
- 🔢 Index numbers simplify complex, ugly numbers, making them easier to read and understand.
- 📈 Index numbers help economists quickly compare data and observe trends, such as whether numbers are rising or falling.
- 💹 Economists often analyze rates of change, such as annual growth or inflation, and index numbers make this analysis easier.
- 🏡 The script provides an example using UK house price data over three years to demonstrate how to convert raw numbers into index numbers.
- ⚖️ To create an index, you must first select a base year, which will always have an index value of 100.
- 🧮 The formula for converting raw numbers into index numbers is: (raw number ÷ base year raw number) × 100.
- 📊 The base year always results in an index value of 100 because dividing the raw number by itself equals 1, and multiplying by 100 gives 100.
- 🔄 Percentage changes between years can be easily calculated by comparing index numbers and applying a simple formula.
- 💡 Index numbers and percentage changes simplify data analysis, making it easier to observe trends and rates of change in large or complex data sets.
Q & A
What are index numbers commonly used for in economics?
-Index numbers are commonly used in economics to simplify and analyze data related to GDP, house prices, productivity, exchange rates, inflation, and other large datasets.
Why do economists prefer using index numbers instead of raw data?
-Economists prefer using index numbers because they simplify large and complex raw numbers, making them easier to interpret and compare. They also help in analyzing rates of change and percentage changes more effectively.
What is the primary benefit of converting raw numbers into index numbers?
-The primary benefit is to make large, complex numbers easier to understand and analyze by standardizing them, often using a base value of 100 for comparison.
How do you convert a raw number into an index number?
-To convert a raw number into an index number, you divide the raw number by the raw number of the base year, then multiply by 100.
What is a base year, and why is it important in calculating index numbers?
-A base year is a reference point used to compare other values. Its index value is always set to 100, and it allows economists to standardize comparisons between different years.
Why does the base year always have an index value of 100?
-The base year has an index value of 100 because the raw number in the base year divided by itself equals 1, which, when multiplied by 100, equals 100.
What is the formula for calculating the percentage change between two index numbers?
-The formula for calculating percentage change is: (Difference between two numbers / Original number) × 100.
How can index numbers help in understanding the rate of change in economic data?
-Index numbers allow for quick and straightforward comparisons of changes over time, making it easier to see trends in growth rates, inflation, or other economic indicators.
In the given example, what is the percentage change in house prices from year one to year two?
-The percentage change in house prices from year one to year two is 2.49%, calculated using the difference between the index numbers 102.49 and 100, divided by 100, then multiplied by 100.
Why are index numbers particularly useful for large datasets in economics?
-Index numbers are useful for large datasets because they reduce complexity, allowing for easier data analysis, visualization, and interpretation of trends and rates of change.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

[Statistik1] Pert 11 Angka Indeks Tak Tertimbang

Cara Menggunakan Fungsi MATCH, INDEX & CHOOSE dalam Ms Excel | Informatika Kelas 8 Bab Analisis Data
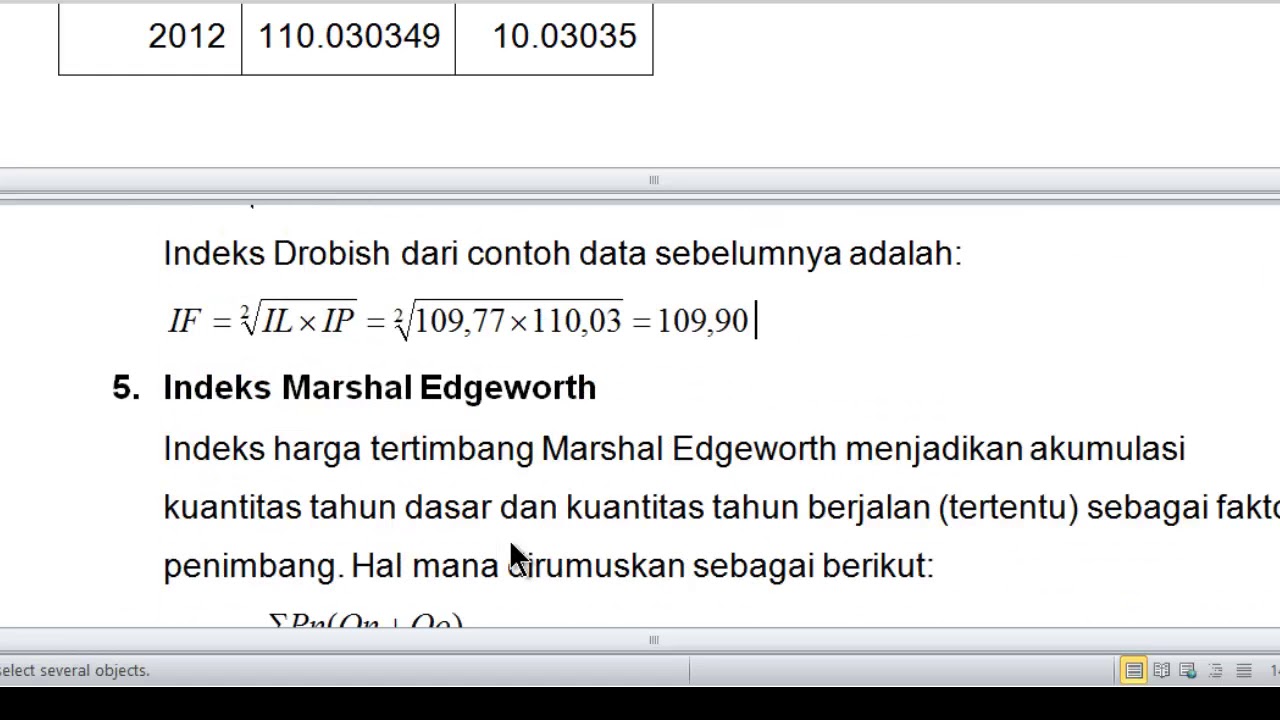
[Statistik1] Pert 12 Angka Indeks Tak Tertimbang

Class 11 Economics (Statistics for Economics) - Book Overview & Complete Strategy | CBSE 2024-25

CPI and Inflation- Macro 2.4

Bab 5 - Angka Indeks - Kelas B
5.0 / 5 (0 votes)
