✅👉 Encontrar Maximos y Minimos Locales en una Grafica
Summary
TLDRThis video explains the concepts of local and absolute maxima and minima of a function. A maximum is the highest point a function reaches, while a minimum is the lowest. Local maxima and minima occur within a specific interval, where the function reaches a peak or a dip but may later surpass those values. Absolute maxima and minima are the highest or lowest points across the entire function. Through examples, the video illustrates how to identify these points on a graph, focusing on distinguishing between local and absolute values.
Takeaways
- 📈 A maximum in a function is the highest point the function reaches before starting to decrease.
- 📉 A minimum in a function is the lowest point the function reaches before starting to increase.
- 🌍 A local maximum is a high point within a certain interval, even if there are higher points elsewhere in the function.
- 🗻 A local minimum is a low point within a specific interval, even if the function decreases further in other areas.
- 🔝 An absolute maximum is the highest value reached by the entire function with no higher values anywhere else.
- 🔻 An absolute minimum is the lowest point reached by the function, with no lower values anywhere else.
- 📊 Local extrema (local maxima and minima) exist within specific intervals of the function, but are not the highest or lowest overall.
- 🧐 To determine if an extremum is local or absolute, it's important to compare it to the entire function, not just an interval.
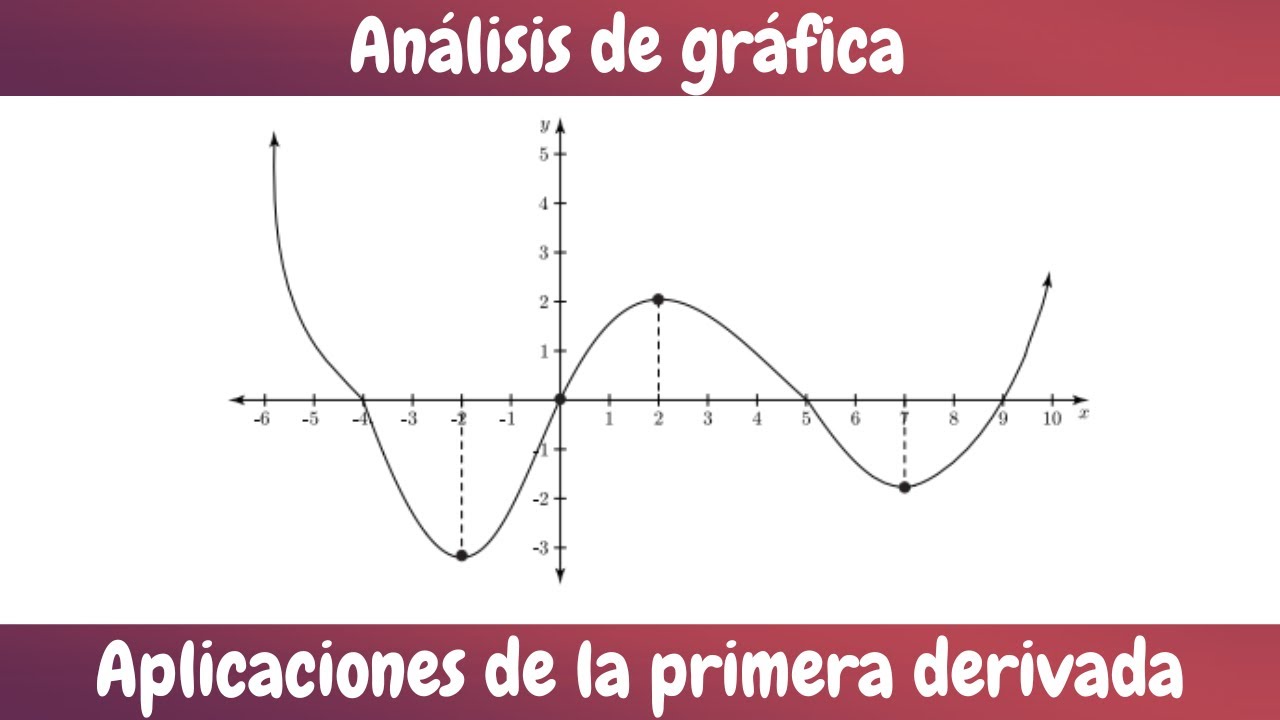
- 📝 In the given example, the point at (0, 2) is a local maximum because the function takes on higher values elsewhere.
- 🔚 The function described tends towards infinity in both directions, meaning it has no absolute maximum or minimum, only local extrema.
Q & A
What is the definition of a maximum in a function?
-A maximum is the highest point that a function reaches. After reaching this point, the function starts to decrease. This point is referred to as a maximum.
What is the definition of a minimum in a function?
-A minimum is the lowest point that a function reaches. After reaching this point, the function starts to increase. This point is referred to as a minimum.
What is the difference between a local maximum and an absolute maximum?
-A local maximum is the highest point within a specific interval of the function, but the function may take higher values elsewhere. An absolute maximum is the highest value that the function reaches across its entire domain.
How can you identify a local minimum?
-A local minimum is identified as the lowest point in a specific interval of the function, but the function may reach lower values outside that interval.
What is an absolute minimum?
-An absolute minimum is the lowest point that a function reaches across its entire domain, meaning no other points in the function are lower than this value.
Can a function have both local and absolute maxima or minima?
-Yes, a function can have both local and absolute maxima or minima. Local extrema occur within specific intervals, while absolute extrema represent the highest or lowest values over the entire domain.
How do you determine if a maximum is local or absolute in a graph?
-To determine if a maximum is local or absolute, examine whether the function takes higher values elsewhere. If there are higher points, it is a local maximum; otherwise, it is an absolute maximum.
How do you determine if a minimum is local or absolute in a graph?
-To determine if a minimum is local or absolute, check if the function takes lower values elsewhere. If there are lower points, it is a local minimum; otherwise, it is an absolute minimum.
What is an example of a function with only local maxima and minima but no absolute extrema?
-An example of a function with only local extrema but no absolute extrema is one that tends toward infinity. In such cases, the function has local maxima and minima, but it doesn't have absolute values because it continues to increase or decrease indefinitely.
Why does a function that tends towards infinity have no absolute maxima or minima?
-A function that tends toward infinity has no absolute maxima or minima because the values continue to increase or decrease without bound. Therefore, there are no highest or lowest points across the entire function.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

08 Aplikasi Turunan | Ekstrim Lokal

Computational Chemistry 3.2 - Energy Minimization
Análisis de gráfica. Primera derivada

CD.28 Criterio de la segunda derivada para máximos y mínimos. Incluye gráfico. Parte 1.

Übersicht f f´ f´´, Zusammenhänge der Funktionen/Graphen, Ableitungsgraphen | Mathe by Daniel Jung

Differentiation (Maxima and Minima)
5.0 / 5 (0 votes)
