08 Aplikasi Turunan | Ekstrim Lokal
Summary
TLDRIn this video, we explore the concept of local extrema in calculus, focusing on both local maximum and minimum points. It explains how to identify these points using the first and second derivative tests. A key insight is that local extrema can occur at stationary points, where the derivative is zero, but not always. The second derivative test further helps distinguish between local maxima and minima based on the concavity of the graph. The video also delves into graphical representations of extrema and their respective conditions for maxima or minima.
Takeaways
- 😀 The concept of extreme values in mathematics includes both maximum and minimum values.
- 😀 Maximum and minimum values can be classified as global or local extrema depending on their occurrence across the entire function or within a specific interval.
- 😀 Local maximum and minimum values occur around a specific interval on the graph, unlike global extrema which are the highest or lowest points overall.
- 😀 A local maximum or minimum is typically found at stationary points where the derivative of the function equals zero.
- 😀 It's important to note that not all stationary points represent local extrema. The behavior of the gradient on both sides of the point must be considered.
- 😀 If the gradient on the left side is positive and on the right side is negative, the point is a local maximum.
- 😀 Conversely, if the gradient on the left side is negative and on the right side is positive, the point is a local minimum.
- 😀 If both gradients are either positive or negative, the point is not a local extremum.
- 😀 The second derivative test helps in confirming the nature of the extremum at a point: if the second derivative is positive, it’s a local minimum; if negative, it's a local maximum.
- 😀 For a local minimum, the graph around the point is concave up, and for a local maximum, it is concave down.
Q & A
What is the difference between global and local extrema?
-Global extrema refer to the highest and lowest points over the entire domain of a function, while local extrema refer to the highest and lowest points within a specific interval or neighborhood on the graph.
What are the conditions for a point to be a local maximum or minimum?
-A point is considered a local maximum if the function value is higher than those of points around it, and a local minimum if the function value is lower than its neighboring points.
What is a stationary point in the context of extrema?
-A stationary point is a point where the derivative of the function equals zero (f'(x) = 0), but it does not always correspond to an extremum. It is a potential location for a maximum or minimum.
What role does the gradient play in identifying local extrema?
-The gradient (or derivative) helps identify local extrema. If the gradient changes sign around a point (from positive to negative or vice versa), that point is likely to be an extremum.
How does the first derivative test help in identifying local extrema?
-The first derivative test involves checking the sign of the derivative on either side of a stationary point. If the derivative changes from positive to negative, it's a local maximum. If it changes from negative to positive, it's a local minimum.
What happens when the first derivative equals zero but the point is not an extremum?
-If the first derivative equals zero but the function does not change from increasing to decreasing or vice versa, then the point is not a local extremum, but might still be a stationary point.
How does the second derivative test help identify local maxima and minima?
-The second derivative test involves checking the sign of the second derivative at a stationary point. If the second derivative is positive, it's a local minimum. If negative, it's a local maximum. If the second derivative equals zero, the test is inconclusive.
What does it mean for a function to be concave up or concave down?
-A function is concave up when its graph forms a 'bowl' shape, which corresponds to a local minimum. It is concave down when its graph forms an 'upside-down bowl' shape, which corresponds to a local maximum.
What is the significance of f'(x) = 0 in determining extrema?
-The condition f'(x) = 0 identifies stationary points, which are potential locations for local maxima or minima. However, further analysis (such as using the first or second derivative test) is required to confirm whether these points are indeed extrema.
Can a function have more than one local maximum or minimum?
-Yes, a function can have multiple local maxima and minima within its domain. These are points where the function reaches a local highest or lowest value within a neighborhood but not necessarily across the entire domain.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Finding Local Maximum and Minimum Values of a Function - Relative Extrema
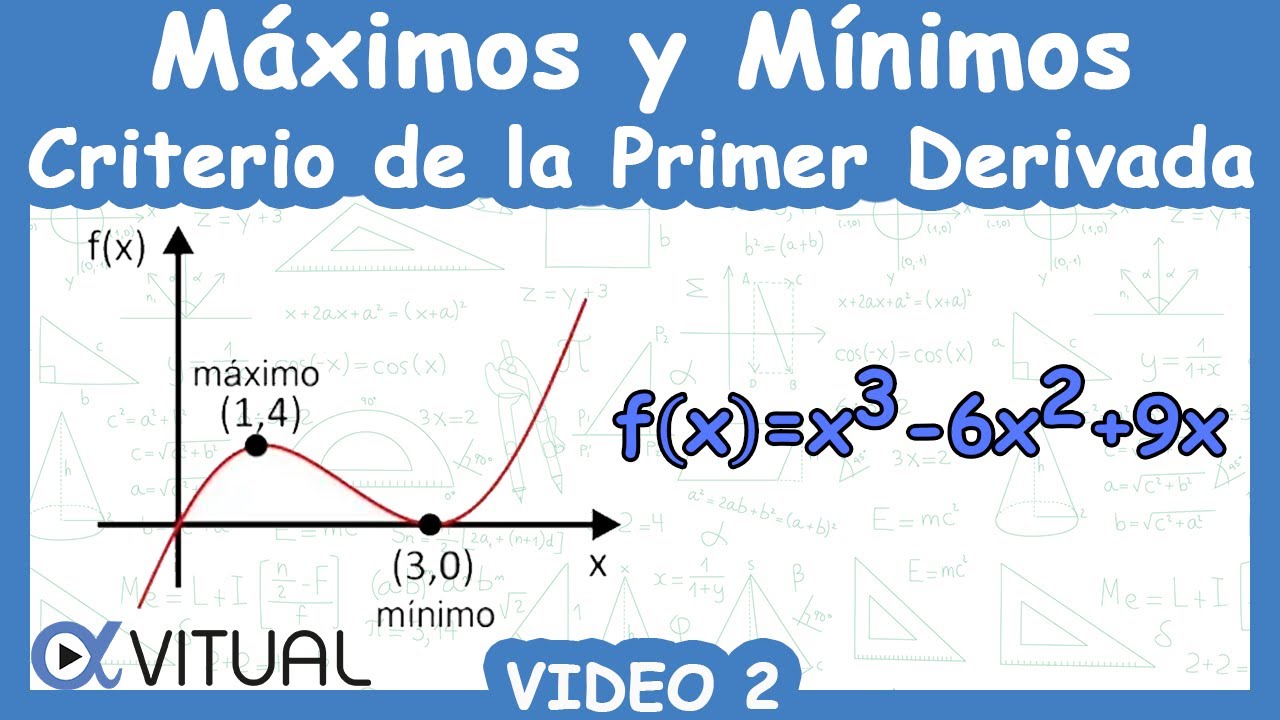
🟦 Máximos y Mínimos de una Función (Criterio de la Primer Derivada) | Video 2
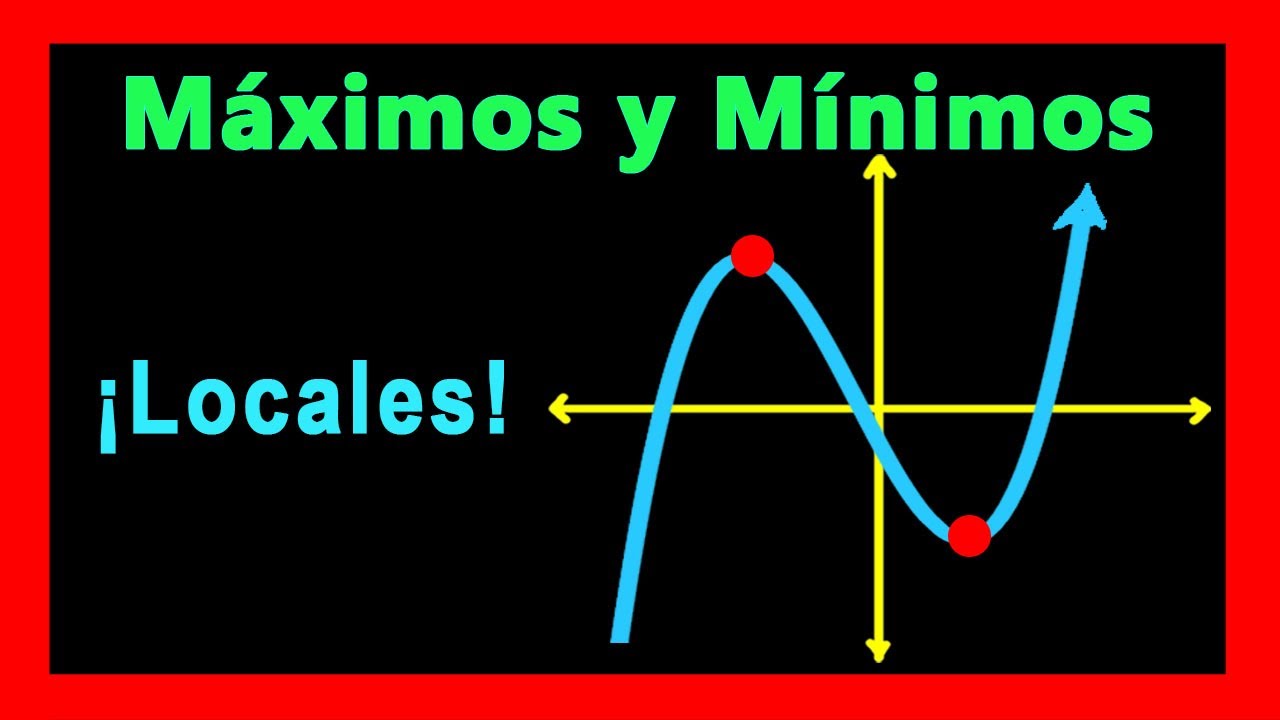
✅👉 Encontrar Maximos y Minimos Locales en una Grafica

Maksimum dan Minimum | Aplikasi Turunan (Part 1) | Kalkulus

Computational Chemistry 3.2 - Energy Minimization

Übersicht f f´ f´´, Zusammenhänge der Funktionen/Graphen, Ableitungsgraphen | Mathe by Daniel Jung
5.0 / 5 (0 votes)