Normal Distribution, Z-Scores & Empirical Rule | Statistics Tutorial #3 | MarinStatsLectures
Summary
TLDRThis video delves into the normal distribution, a key probability distribution used to understand data sampling from a population. It uses the example of human height, assuming a mean of 175 cm and a standard deviation of 10 cm, to explain the distribution's bell-shaped curve. The video highlights the 68-95-99.7 rule, illustrating how data points cluster around the mean. It then explores calculating probabilities, such as the likelihood of an individual being taller than 190 cm, by converting raw scores into z-scores, a method of standardizing data. The focus is on grasping the concepts rather than the mechanics of using a Z-table or software.
Takeaways
- 📊 The normal distribution is a theoretical probability distribution that models the distribution of a population's data.
- 📈 The mean of the normal distribution is the center, and the standard deviation describes the spread or variability of the data.
- 📉 As standard deviation increases, the normal distribution becomes wider; as it decreases, the distribution becomes narrower.
- 🔢 The 68-95-99.7 rule states that approximately 68%, 95%, and 99.7% of the data fall within one, two, and three standard deviations from the mean, respectively.
- 👤 The probability of an individual's height being greater than a certain value can be calculated using the normal distribution.
- 🔄 Standardizing a value means converting it into how many standard deviations it is from the mean.
- 🌐 Standardizing does not change the shape of the distribution; it only changes the scale of measurement.
- 📚 The concept of standardizing is akin to a unit conversion, making it easier to understand the distribution's properties.
- 📊 The Z-score represents how many standard deviations an observation is from the mean.
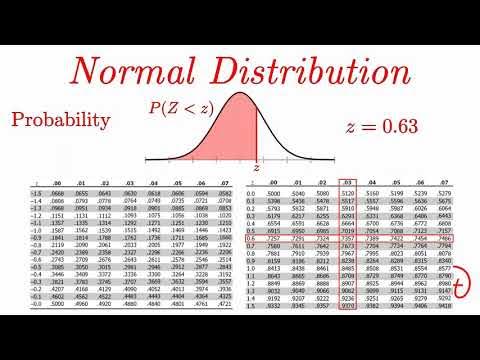
- 🔎 To find the probability of an observation beyond a certain value, one can use a Z-table or statistical software.
Q & A
What is the normal distribution?
-The normal distribution is a theoretical probability distribution that is bell-shaped and symmetric about its mean, allowing us to understand what can be expected when collecting a sample of data from a population.
What are the characteristics of a normal distribution?
-A normal distribution is characterized by its mean, which centers the distribution, and its standard deviation, which indicates how spread out or variable the data is. The larger the standard deviation, the wider the distribution; the smaller the standard deviation, the narrower it becomes.
What is the significance of the 68-95-99.7 rule in the context of the normal distribution?
-The 68-95-99.7 rule, also known as the one-two-three standard deviation rule, is a handy way to do quick calculations. It states that approximately 68% of observations fall within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.
How does the mean of the normal distribution relate to the data?
-The mean of the normal distribution is the center of the distribution, and it represents the average value of the data. Data points are symmetrically distributed around this mean.
What does the standard deviation tell us about the normal distribution?
-The standard deviation of the normal distribution tells us about the spread or variability of the data. A larger standard deviation indicates a wider distribution, while a smaller standard deviation indicates a more concentrated distribution around the mean.
What is the probability that a randomly selected individual from a population with a mean height of 175 cm and a standard deviation of 10 cm is taller than 190 cm?
-The probability of an individual being taller than 190 cm can be calculated by standardizing the height (190 cm) to a Z-score and then looking up the corresponding probability in a Z-table or using statistical software. For a height of 190 cm, it is 1.5 standard deviations above the mean, which corresponds to approximately a 6.7% chance.
How is standardizing a value in the normal distribution done?
-Standardizing a value in the normal distribution involves subtracting the mean from the value and then dividing by the standard deviation. This converts the original scale to a scale in terms of standard deviations from the mean.
What is a Z-score and how is it used in the context of the normal distribution?
-A Z-score represents how many standard deviations an observation is from the mean. It is used to standardize data points, allowing for comparison and calculation of probabilities across different normal distributions.
Why is the concept of unit conversion used to explain standardizing in the normal distribution?
-The concept of unit conversion is used to explain standardizing because it helps to make the process intuitive. Just as converting from centimeters to inches does not change the shape of the distribution, standardizing using standard deviations as a unit of measurement also preserves the normal distribution's shape.
How can we find the probability associated with a Z-score?
-The probability associated with a Z-score can be found using a Z-table, which provides the area to the left of the Z-score, or by using statistical software that can calculate the area under the normal distribution curve for a given Z-score.
What is the practical implication of knowing the probability of an individual being 190 cm or more in a population?
-Knowing the probability of an individual being 190 cm or more can help in various applications such as predicting the likelihood of certain traits in a population, understanding genetic variations, or even in designing infrastructure like public transportation to accommodate taller individuals.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Probabilitas dan Statistik: 8.6 Central Limit Theorem

Samples from a Normal Distribution | Statistics Tutorial #4 | MarinStatsLectures

Sample and Population in Statistics | Statistics Tutorial | MarinStatsLectures
Normal Distribution EXPLAINED with Examples

Amostras e Erro Amostral Bioestatística #7

Sampling Distributions (7.2)
5.0 / 5 (0 votes)
