Boundary Conditions

Summary

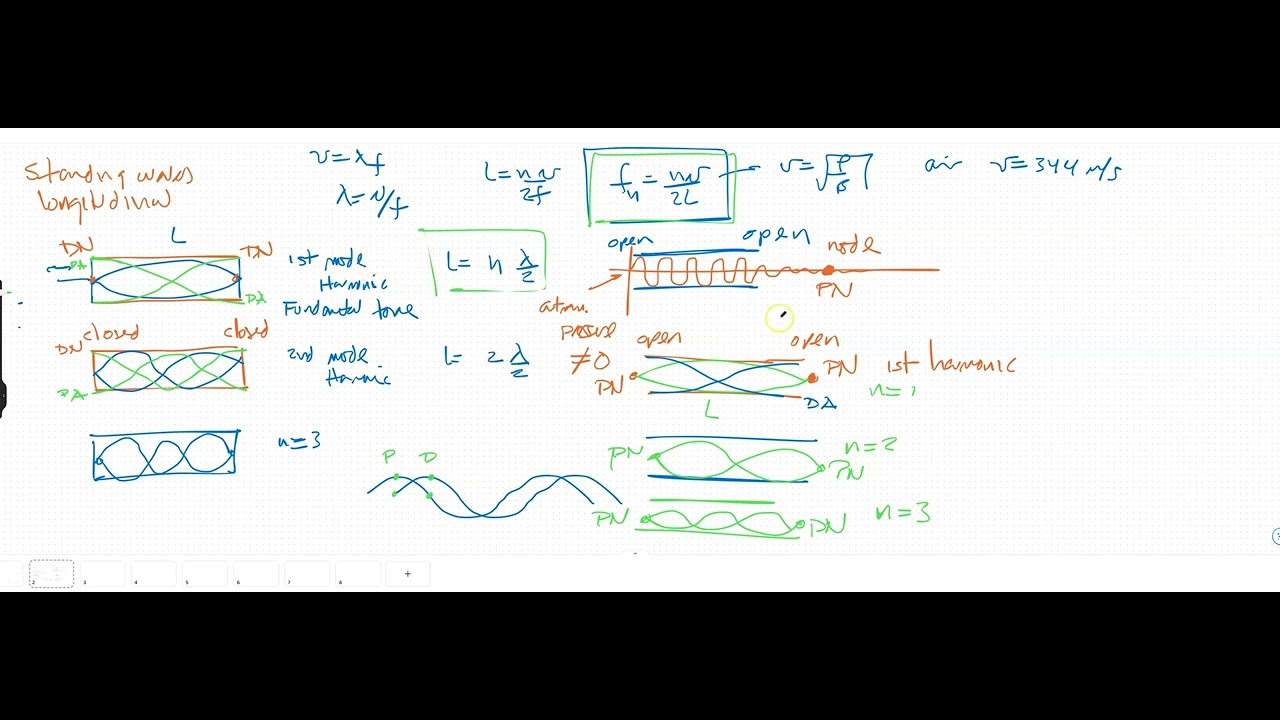
The script discusses the formation of standing waves, emphasizing the importance of nodes and anti-nodes at boundary positions. It explains how specific frequencies and wavelengths create standing waves on a string, with the length of the string being a critical factor. The script introduces the concept of harmonics, illustrating the fundamental frequency and overtones, and how they relate to the number of half-wavelengths fitting the string's length. The equation for harmonic frequency is derived, showing the relationship between string length, wave speed, and tension.

Takeaways

• 🎓 The creation of a standing wave is dependent on the boundary conditions and the nature of the wave's reflection.
• 🔍 A standing wave is formed when the last molecule at the boundary is a node, preventing energy loss to the surroundings.
• 🌊 The correct frequency and wavelength are crucial for the formation of a standing wave on a string.
• 📏 The length of the string must be an integer multiple of half the wavelength (λ/2) to support a standing wave.
• 🔢 The condition for the string length to support standing waves can be expressed as L = nλ/2, where n is the harmonic number.
• 🎵 Different harmonics (fundamental, first overtone, second overtone, etc.) correspond to different modes of oscillation.
• 📉 The first harmonic is also known as the fundamental tone, while higher harmonics are called overtones.
• 🔄 The harmonic frequency that matches the string's length and generates a standing wave can be calculated using the formula f = nV/λ.
• 🧮 The speed of a transverse wave on a string is given by the formula V = sqrt(Tension/μ), where Tension is the tension in the string and μ is the linear mass density.
• 🔄 The number of half-wavelengths that fit into the string determines the number of loops or the harmonic number.

Q & A

What is a standing wave?

A standing wave is a wave pattern that appears to be stationary, where the crests and troughs remain in the same position over time. It occurs when two waves of the same frequency and amplitude travel in opposite directions and superimpose on each other.

Why is it important for the last molecule in a standing wave to be a node?

The last molecule being a node is important because it means the molecule does not need to move up and down, thus no work is done on the wall, and the molecule does not lose energy trying to move.

What is a node in the context of standing waves?

A node is a point in a standing wave where the displacement of the medium is zero. It is a point of no movement, occurring at the boundaries of the medium where the wave is reflected.

What is the relationship between the length of a string and the wavelength for a standing wave to be formed?

For a standing wave to be formed, the length of the string must be an integer multiple of half the wavelength (λ/2, λ, 3λ/2, etc.), corresponding to different harmonics.

What are the first three harmonics of a standing wave?

The first three harmonics are the fundamental (n=1), the first overtone (n=2), and the second overtone (n=3). These correspond to one, two, and three half wavelengths fitting into the length of the string.

How is the frequency of a standing wave related to its wavelength and the length of the string?

The frequency of a standing wave is related to its wavelength and the length of the string by the equation f = nV/(2L), where n is the harmonic number, V is the wave speed, and L is the length of the string.

What is the significance of the term 'harmonic' in the context of standing waves?

A harmonic refers to the different modes of oscillation of a standing wave, each with a specific frequency that is an integer multiple of the fundamental frequency. The harmonic number indicates the number of half-wavelengths that fit into the string.

What is the fundamental tone and how does it relate to the first harmonic?

The fundamental tone is the lowest frequency at which a standing wave can be formed on a string, corresponding to the first harmonic, where the string's length equals half the wavelength.

What is the speed of a transverse wave on a string and how is it calculated?

The speed of a transverse wave on a string is calculated by the formula V = sqrt(T/μ), where T is the tension in the string and μ (mu) is the linear mass density of the string.

How can you determine the valid frequencies for creating a standing wave on a string?

Valid frequencies for creating a standing wave on a string are those that result in wavelengths that are integer multiples of half the string's length, allowing for the formation of nodes and antinodes at the correct positions.

What happens to the energy of a wave if the frequency does not match the length of the string to create a standing wave?

If the frequency does not match the length of the string for a standing wave, the energy of the wave is wasted trying to move the molecules beyond their fixed positions, and the wave does not sustain.