The Fourier Transform in 15 Minutes

Summary

This video script offers a concise introduction to the Fourier Transform, explaining how it transforms functions from the time or space domain to the frequency domain. It discusses the concept of basis functions, using cosines and sines to express any function in frequency space. The script also touches on the historical context of Fourier's work, the mathematical derivation of the transform, and its applications in solving differential equations. The Fourier Transform is depicted as a powerful tool for analyzing signals and functions, decomposing them into their constituent frequencies.

Takeaways

• 📚 The Fourier Transform is a mathematical technique that transforms a function of one variable (like time) into a function of another variable (like frequency).
• 🔄 It provides a way to switch between the time domain and the frequency domain, allowing for analysis of frequency components of a signal.
• 🌌 The basis of the Fourier Transform is cosines and sines, which are mathematically orthogonal and can be used to express any function in the frequency domain.
• 🔢 The Fourier Transform can be thought of as a way to decompose a function into its constituent frequencies, similar to how currency is broken down into smaller units.
• 🧮 It's possible to use Euler's equation to switch between using cosines and sines and complex exponentials in the Fourier Transform.
• 📊 The Fourier Transform can represent a single sinusoid as a single peak in the frequency domain, while more complex signals like a square wave require multiple frequencies.
• 🌉 The concept of basis functions extends from Cartesian coordinates to the frequency domain, where cosines and sines serve as the basis functions.
• 🌟 The Fourier Transform is particularly useful for solving differential equations because it aligns with the solutions often involving exponentials.
• 🔄 The Fourier series is an extension of the Fourier Transform to periodic functions, and it can be used to represent any periodic function as a sum of sines and cosines.
• 📐 The derivation of the Fourier Transform involves moving from discrete sums to continuous integrals, which is a key step in generalizing from periodic to non-periodic functions.

Q & A

What is the Fourier Transform?

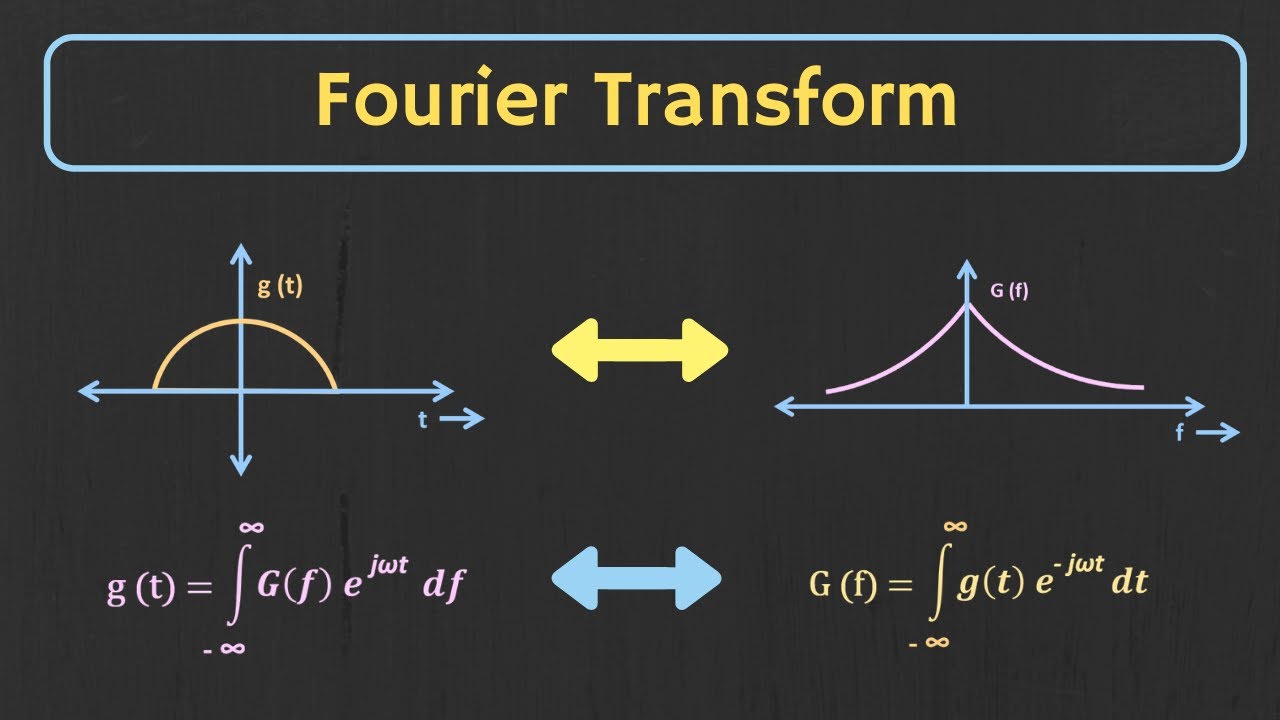
The Fourier Transform is a mathematical technique that transforms a function of one variable, often time, into a function of another variable, frequency. It decomposes a function into its frequency components, allowing for analysis in the frequency domain.

What is the inverse Fourier Transform?

The inverse Fourier Transform is the process of converting a function from the frequency domain back to the time domain. It allows us to recover the original function from its frequency components.

How does the Fourier Transform change the basis of a function?

The Fourier Transform changes the basis of a function from time or space to cosines and sines, which are mathematically orthogonal and can be used to express every point in frequency space.

What is the significance of basis functions in the context of the Fourier Transform?

Basis functions, such as cosines and sines, are significant because they provide a way to express any function in the frequency domain. They are orthogonal, which allows for the decomposition of complex signals into simpler components.

Why is the Fourier Transform useful for solving differential equations?

The Fourier Transform is useful for solving differential equations because it often simplifies the equations by transforming them into the frequency domain, where the basis functions are cosines and sines or complex exponentials, which are easier to handle.

How does the Fourier Transform relate to the concept of Fourier series?

The Fourier Transform is an extension of the concept of Fourier series. While Fourier series deals with periodic functions, the Fourier Transform generalizes this to non-periodic functions by extending the concept to infinite or non-periodic signals.

What is the physical interpretation of the Fourier Transform?

Physically, the Fourier Transform tells us the frequency components of a function or signal. It can reveal the frequencies present in a time-domain signal, which is useful for signal processing and analysis.

How does Euler's equation relate to the Fourier Transform?

Euler's equation allows us to represent cosines and sines as complex exponentials. This representation is useful in the Fourier Transform because it simplifies the mathematical expressions and allows for easier manipulation of the transform.

What is the difference between the Fourier Transform of a single sinusoid and a square wave?

The Fourier Transform of a single sinusoid results in a single peak or delta function at the frequency of the sinusoid, indicating a single frequency component. In contrast, the Fourier Transform of a square wave results in many frequencies of different amplitudes, indicating that a square wave is composed of multiple frequency components.

Why does the Fourier Transform use complex exponentials instead of just cosines and sines?

The Fourier Transform uses complex exponentials because they can represent both cosines and sines in a single expression, simplifying the mathematical process. This is possible because the sine components integrate to zero in the Fourier Transform.

How is the Fourier Transform derived from the Fourier series?

The Fourier Transform is derived from the Fourier series by extending the period of the function to infinity, changing the summation to an integral, and replacing the discrete frequency components with a continuous variable. This process involves letting the period go to infinity and the frequency spacing go to zero.

Outlines

00:00

📚 Introduction to Fourier Transform

The speaker begins by introducing the concept of the Fourier Transform, emphasizing its ability to transform a time-based function into a frequency-based one. The inverse Fourier Transform does the opposite, translating frequency back to time. The Fourier Transform is likened to a change of basis, expressing functions in terms of sines and cosines, which are mathematically orthogonal. The speaker also explains that the Fourier Transform can be extended to spatial functions, changing spatial domain to spatial frequency domain. The concept of basis functions is introduced, drawing parallels to coordinate systems and suggesting that sines and cosines can be used to express any point in 'frequency space.' A brief mention of Euler's equation is made, hinting at the transition from sines and cosines to complex exponentials.

05:03

🔍 Physical Significance and Applications

This paragraph delves into the physical significance of the Fourier Transform, highlighting its roots in Fourier series, which allows any periodic signal to be expressed as a combination of sines and cosines of different frequencies. The speaker explains that the Fourier Transform extends this concept to non-periodic functions, providing frequency components of a signal. The mathematical manipulations become simpler in the frequency domain compared to the time or spatial domain. Examples are given, contrasting a single sinusoid with a square wave, showing how the latter requires many frequencies to be fully represented. The idea of approximating functions globally using an infinite series of sines and cosines is introduced, contrasting with local approximations using power series.

10:04

🔗 Derivation and Relationship to Laplace Transform

The speaker outlines the derivation of the Fourier Transform, starting from Joseph Fourier's work on periodic functions. The process involves moving from discrete to continuous components and extending the period to infinity, transitioning from sums to integrals. The importance of the dummy variable and the shift to complex exponentials using Euler's equation is emphasized. The Fourier Transform is then connected to the Laplace Transform, noting that while the Fourier Transform uses complex exponentials, the Laplace Transform uses both real and complex exponentials, thus encompassing solutions to differential equations.

15:07

📢 Conclusion and Call to Action

In the concluding paragraph, the speaker summarizes the discussion and encourages viewers to share the video, subscribe to the channel, and visit the website for more information. The tone is inviting, suggesting a community of learners interested in physics and mathematics.

Keywords

💡Fourier Transform

The Fourier Transform is a mathematical technique that transforms a function of time (or space) into a function of frequency. It is used to analyze the frequency components of a signal. In the video, the Fourier Transform is introduced as a way to move from the time domain to the frequency domain, allowing for a different perspective on the function. For example, the script mentions that if you input a function of time, the transform will output a function of frequency.

💡Inverse Fourier Transform

The Inverse Fourier Transform is the process of converting a function from the frequency domain back to the time (or spatial) domain. It is the reverse operation of the Fourier Transform. The video script explains that if you input a frequency through the inverse transform, you get back a function of time, essentially reversing the process described by the Fourier Transform.

💡Frequency Domain

The frequency domain is a representation of a signal in terms of frequency components. It is a way to analyze how much of each frequency is present in a signal. The video script discusses how the Fourier Transform changes the basis of a function from time to frequency, hence moving it into the frequency domain, where it can be analyzed in terms of its constituent frequencies.

💡Time Domain

The time domain is a representation of a signal as it varies over time. It is the standard way of looking at signals where the function's values are plotted against time. The video script contrasts the time domain with the frequency domain, explaining that the Fourier Transform allows for a transformation from time-based functions to frequency-based functions.

💡Basis Functions

Basis functions are used to express a function in terms of a set of fundamental functions. In the context of the video, cosines and sines are the basis functions used in the frequency domain to represent any function. The script explains that these basis functions are mathematically orthogonal, which allows them to be used to express every point in frequency space.

💡Orthogonality

Orthogonality in mathematics refers to a relationship between two vectors or functions where they are perpendicular to each other. In the video, orthogonality is discussed in the context of cosine and sine functions, which are mathematically orthogonal and can be used as basis functions for expressing any point in space, similar to how Cartesian coordinates are used in physical space.

💡Euler's Equation

Euler's Equation is a fundamental principle in mathematics that states that e^(ix) = cos(x) + i*sin(x), where i is the imaginary unit. The video script mentions Euler's Equation in the context of the Fourier Transform, showing how it allows for a transition from using cosine and sine to complex exponentials, simplifying the mathematical representation of the transform.

💡Complex Exponentials

Complex exponentials are mathematical expressions involving the exponential function of a complex number. In the video, complex exponentials are introduced as an alternative to cosines and sines in the Fourier Transform, leveraging Euler's Equation. They are used to simplify the mathematical expressions and calculations involved in the transform.

💡Fourier Series

The Fourier Series is a method for representing a function as an infinite sum of sines and cosines. It is a foundational concept for the Fourier Transform, as it extends the idea of decomposing a function into its frequency components. The video script explains that any periodic signal can be expressed as a combination of sines and cosines of varying frequencies, which is the core idea behind the Fourier Series.

💡Differential Equations

Differential Equations are equations that relate a function to its derivatives. In the video, it is mentioned that all differential equations are solved using real and complex exponentials, and that the Fourier Transform is useful in solving these equations because it decomposes functions into their frequency components, which are the basis for these solutions.

💡Laplace Transform

The Laplace Transform is a mathematical transform used to analyze the behavior of a system in the complex plane, often used to solve differential equations. The video script relates the Fourier Transform to the Laplace Transform, noting that while the Fourier Transform uses complex exponentials, the Laplace Transform uses both real and complex exponentials, thus encompassing a broader set of solutions to differential equations.

Highlights

Introduction to the concept of the Fourier Transform

Fourier Transform and its inverse are mathematical tools that transform functions from time to frequency domain

The Fourier Transform changes the basis of a function to one of cosines and sines

Fourier Transform expresses functions in the frequency domain using orthogonal basis functions

Cosines and sines are mathematically orthogonal, allowing them to express every point in frequency space

The Fourier Transform can be thought of as a method to decompose a function into its frequency components

Fourier Transform is useful for solving differential equations involving real and complex exponentials

Fourier Transform extends the concept of Fourier series to non-periodic functions

The physical interpretation of the Fourier Transform is that it reveals the frequency components of a signal

Fourier Transform allows for complicated mathematical manipulations to be performed more easily in the frequency domain

An example of the Fourier Transform of a single sinusoid results in a delta function at the frequency of the sinusoid

The Fourier Transform of a square wave results in many frequencies of different amplitudes

Fourier suggested that an infinite series of cosines and sines could approximate a function globally

The Fourier Transform is derived from the Fourier series by extending the period to infinity

The Fourier Transform can be expressed using complex exponentials through Euler's equation

The Fourier Transform can be split into different forms, including positive and negative frequency components

The Fourier Transform can be reverted back to the linear frequency domain

The importance of the dummy variable 't' in the derivation of the Fourier Transform

The Fourier Transform is a powerful tool for analyzing and manipulating functions in various domains

Transcripts

okay in this video I'm going to

introduce the concept of the free

transform in as little time as possible

if you're looking for a more detailed or

thorough approach you should see my

website University Physics Torrio's comm

to begin with I've written the free

transform and it's inverse on front of

you knows what happens and I will speak

about a more in-depth that we input a

function of time and through the

integral transform we get out one of

frequency if we input one a frequency

through the integral transform we get

out back one of time if we put in one

there was a function of space in here we

get back out one that is a function of

spatial frequency so we get the inverse

of the units of whatever function went

in the bottom line up front about the

Fourier transform is that it transforms

a function of one particular variable

let's say time which might be measured

in seconds and this would live in the

free or excuse me

in the time domain and it will be

transformed into a second function which

lives in the frequency domain and will

be measured in per seconds or Hertz

where the input function was one of time

also the Fourier transform changes the

basis of your function to one of cosines

and sines another way of looking at it

is that the Fourier transform does two

things it gives you a domain change to

the frequency domain so where your input

function was one of time say your output

function will be one of frequency

measured in per seconds if input

function is one of meters the output

function will be one of per meter or

spatial frequency furthermore the

Fourier transform expresses your

function in the frequency domain using

cosines and sines as the basis functions

the concept of basis functions shouldn't

be new to you because we use I had J hat

K hat in the Cartesian coordinate system

to express every point we also might use

spherical polar coordinates

or we might choose cylindrical

coordinates all different ways of

expressing the same points in the space

and they all have their different uses

cosines and sines can be used to express

points as well because they are

mathematically orthogonal to each other

we know of course that physically I J

and K are perpendicular orthogonal to

each other but mathematically cosine and

sine can be shown to be orthogonal to

each other and therefore offer the

possibility of using those as a way of

expressing every point in your space

namely frequency space how does the free

transform work but if I were to ask you

how many cents do you have in more

neural you would divide one euro by one

Santa get 100 you do the same thing to

find out that there are 88 and 64 so if

you wanted to find out how many six

heart signals are your in your in your

initial signal perhaps you would divide

your initial signal by six Hertz is that

what the Fourier transform is doing now

I have an important aside which I'm

actually not going to dwell on if you

require you can pause the video and read

it yourself within the Fourier transform

integrals there exist product of cosines

and sines which using clever

trigonometric identities can be written

as a single cosine within the Fourier

integrals any sine components will

integrate to 0 therefore we can actually

add as an eye time sine to the cosine we

found above and integrate it and it will

give us the exact same answer as a

single cosine this allows us to utilize

Euler's equation and go from using

cosine and sine to complex Exponential's

that is the end of my aside so the

purpose of the aside was to show that we

needn't the free integrals integrating

cosine is the exact same as integrating

a complex exponential because the sine

will always integrate to 0 therefore

going back to our question if we start

with rational function f of T if we

divide that by cosine 60 which is a

signal with frequency 6

the same as dividing it by e to the I 60

which is of course the same as

multiplying it by e to the minus I 60

but this is only computed as one

particular point or valid at one

particular point so if we integrate it

for all time we get the Fourier

transform of that particular frequency

or more generally we can think of this

using the angular frequency Omega of

course it's easy to switch between the

angular frequency and the linear

frequency by the factor of 2 pi why do

we bother using the Fourier transform

physically the free transform will tell

you the frequency components of your

function or signal this all stems from

the concept of Fourier series which say

that any signal any periodic signal

actually can be expressed as a

combination of sines and cosines of

varying frequencies so the Fourier

transform is simply extending the

concept of the Fourier series to

infinity or to a periodic functions and

will still give you the frequency

components of your signal mathematically

the free transform often allows you to

perform complicated mathematical

manipulations in the 48 main much

simpler than there would be in the

original time or spatial domain we speak

of decomposing our function into its

frequency components in the Fourier

domain next I'd like to show you some

free transforms if my input function is

a single sinusoid of frequency 20 the

Fourier transform will give me a single

peak or a delta function at the

frequency of 20 in the Fourier domain so

it will show me the single frequency

that is in the input function this is in

contrast to an input square wave if I

perform the input if I perform the

Fourier transform of a square wave I get

many many many frequencies of different

amplitudes and at the higher frequencies

we require Larry

amplitudes the point is that a square

wave requires many many frequencies in

order to fully represent it whereas a

single cosine only requires one the

Fourier transform has decomposed my

square wave into its many frequency

components you should have seen during

your studies that power series can be

used to approximate functions with an

input with an input variable X you go

through your power series and you come

out at the value of your function at

that particular point in space power

series however only approximate

functions locally the usual power series

used in order to approximate functions

at the Taylor and Maclaurin however we

want to expand this to approximate a

function globally Joseph Fourier

suggested that cosines and sines inside

an infinite series could expand or

excuse me could approximate a function

globally so if you can accept that a

power series of the following form is a

babe able to approximate your function

locally then you should have no

difficulty in accepting that a power

series should be able to power series

and cosines and sines or Fourier series

can approximate your function globally

in Cartesian space we usually use the

unit vectors I have j HK hat to

represent every point and they have the

following orthogonality properties here

they can express every point because

they are in fact mathematically and

physically in orthogonal as I said

earlier on cosine and sine are

mathematically are taught orthogonal and

can do the same job however in order to

represent a point in space in 2d space

we only require two basis vectors but if

you use cosines and sines we require an

infinite number of basis functions and

I've written them here we know the cost

of not is 1 the sine if not is not and

thereafter we increment the frequency

in the event that you need some

convincing let's look at a square wave

we start off with a single sinusoid of

one frequency we triple its frequency

and thereafter we add many different

sinusoids of different frequencies of

odd number what we see is the more

different sinusoids of varying frequency

we add the closer we come to properly

representing a square wave when we

started out with a single sinusoid the

other reason we are interested in using

sinusoids as a basis is that their

argument must be dimensionless so where

we have an input function of time let's

say this means that K must be of units

per second it is a frequency if the

input function is one of position then

the output function or the K would be of

spatial frequency so using functions

rather than vectors gives us access to

frequency components in frequency space

also all differential equations are

solved using real and complex

Exponential's the Fourier series and the

Fourier transform will always be useful

therefore in solving differential

equations because the basis will be the

cosines and sines or the complex

Exponential's in fact if we extend this

concept to real Exponential's we get the

Laplace transform so that's the

relationship between the Fourier and

Laplace transform Fourier transform only

uses complex Exponential's till the plas

transform uses both and as a result it

uses both of the solutions to

differential equations next I'd like to

very quickly illustrate how we derive

the Fourier transform Joseph Fourier

showed that all two pi periodic

functions have a Fourier transform which

is given by the following equations this

concept is easily extended to periodic

functions of period twice L as done by

this particular equation

as a matter of interest the expressions

here will show you how to go between

cosine of Omega T and cosine KX or move

in between time and space if you like

so this equation here is our Fourier

series using Omega instead of the linear

frequency nu the next thing to do is to

insert the integrals which will

calculate a sub 0 a sub N and B sub n

I've done so here in the equations in

the red box note that this is a periodic

function and therefore giving it the

subscript of L furthermore I'm using a

dummy variable inside the integrals for

a n BN and a 0 this use or this

technique is of great use and will be

seen it's it's importance will be seen

later this equation has discrete

components due to the summation but the

discreet variable is Omega sub n through

the definition of Omega we can therefore

calculate Delta Omega which is Omega n

plus 1 minus Omega n which turns out to

be PI over L this value 4 PI over L can

be substituted in here and in here and a

periodic function can be thought of as a

periodic function with an infinite

period therefore what we do is we extend

the period of our function to infinity

or let Delta Omega go to 0 and just like

the Riemann sums the infinite sum will

become an infant art with the infinite

sum will become an integral and Delta

Omega would become D Omega however in

the integral for a sub 0 there is no

summation and as a result as Delta MA

goes to 0 this will simply become 0 and

we get no constant term what we are left

with is the following equation on the

top of your screen

note that the integral goes from 0 to

infinity and

we've gone from a Seban and B sub n to a

and B of Omega it is important to note

however that a and B of Omega still

involve their own infinite integrals as

discussed earlier on in the video

because of a and Omega and B of Omega we

essentially have a product of cosines in

here and a product of science here which

as we said earlier on can be

re-expressed as a single cosine

thereafter we look at the integral here

which is even in cosine there if we

extend the lower limit to negative

infinity and half the answer this gives

us the factor of 2 here the 1 over pi is

a legacy issue from the Fourier series

finally using the trick I discussed

earlier on in the video where we

introduce the sine which is going to

integrate to 0 anyway we can now

incorporate Euler's equation and move

from trigonometric cosine and sine to

complex Exponential's note the

importance of our dummy variable R which

you've had been left at t wouldn't have

allowed us to guess to this particular

expression next we split the exponential

between a positive and negative

exponential we note that each the - our

a to the I Omega T here can be separated

out and we are left with our Fourier

transform pair we can split our Fourier

transform pair in three different ways

which I've written here or we can revert

back to the linear frequency here note

that I can move the constant term 1 over

2 pi between the forward and inverse

transforms no problem so that's all I've

got to say about that thanks for

watching please pass it on to your

friends subscribe to my channel and you

might also give a comment on university

physics tours calm