Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Summary
TLDRThis video script delves into the concept of limits in calculus, explaining how they underpin the definition of derivatives. It clarifies the formal definition of a derivative using limits to avoid paradoxical infinitesimals, introduces the epsilon-delta definition for a rigorous understanding of limits, and concludes with L'Hopital's Rule—a trick for computing limits involving indeterminate forms like 0/0. The script aims to build intuition and confidence in calculus concepts, emphasizing the importance of limits in calculus.
Takeaways
- 📘 The concept of a limit is intuitively similar to the idea of something 'approaching' another value.
- 🔄 The formal definition of a derivative aligns with the intuitive understanding of limits and the concrete use of 'dx'.
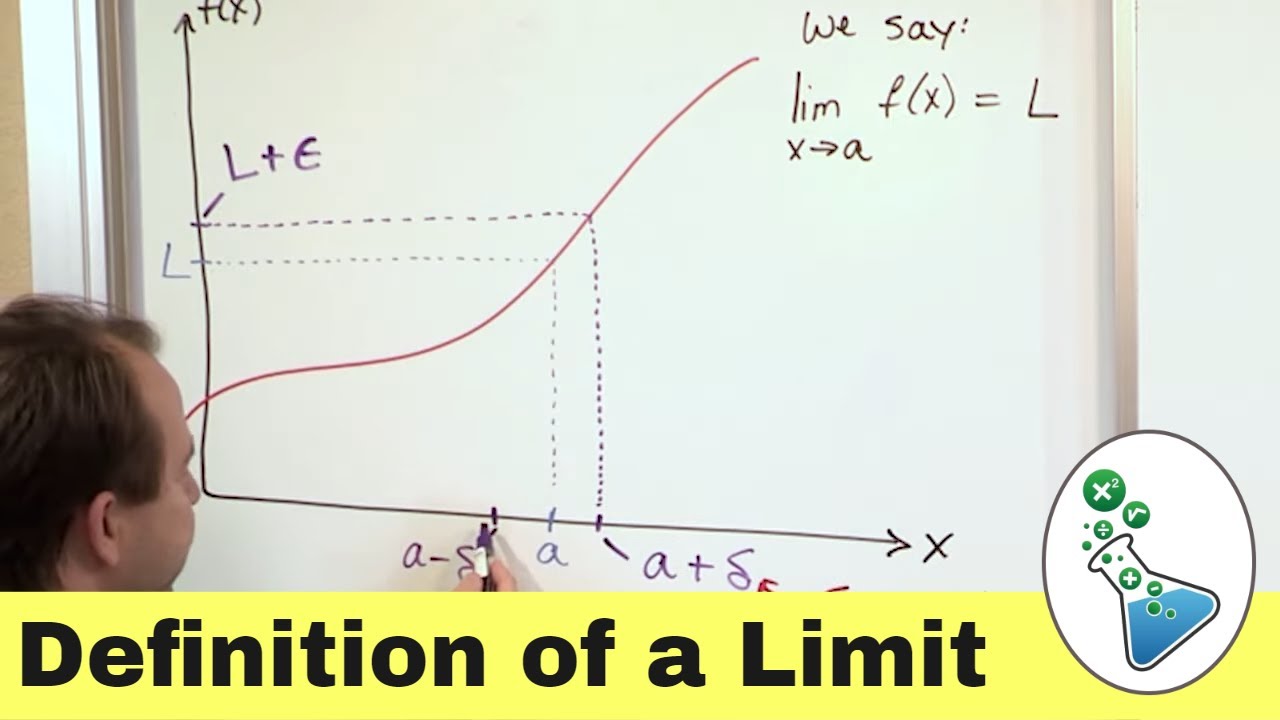
- 📐 The epsilon-delta definition of limits provides a rigorous mathematical framework to describe 'approaching' values.
- 🚫 Limits avoid the paradoxical concept of infinitesimals by focusing on the behavior as changes approach zero.
- 📉 The limit of a function at a certain point is the value the function output approaches, even if the function is undefined at that point.
- 🔍 The epsilon-delta definition helps to determine if a limit exists by examining the behavior of input and output ranges around the limit point.
- 📌 The concept of limits is fundamental to calculus and is used to define derivatives formally.
- 🔄 L'Hopital's Rule is a clever trick for computing limits when faced with expressions that result in '0/0' indeterminate forms.
- 📚 L'Hopital's Rule involves taking the derivatives of the numerator and denominator and evaluating them at the problematic point.
- 🎓 Understanding limits and L'Hopital's Rule is crucial for a deeper comprehension of calculus and its applications.
Q & A
What is the main focus of the video script?
-The main focus of the video script is to explain the concept of limits in calculus, its formal definition, and its relation to the derivative. It also aims to clarify the epsilon-delta definition of limits and introduces L'Hopital's rule for computing limits.
How does the script define the derivative?
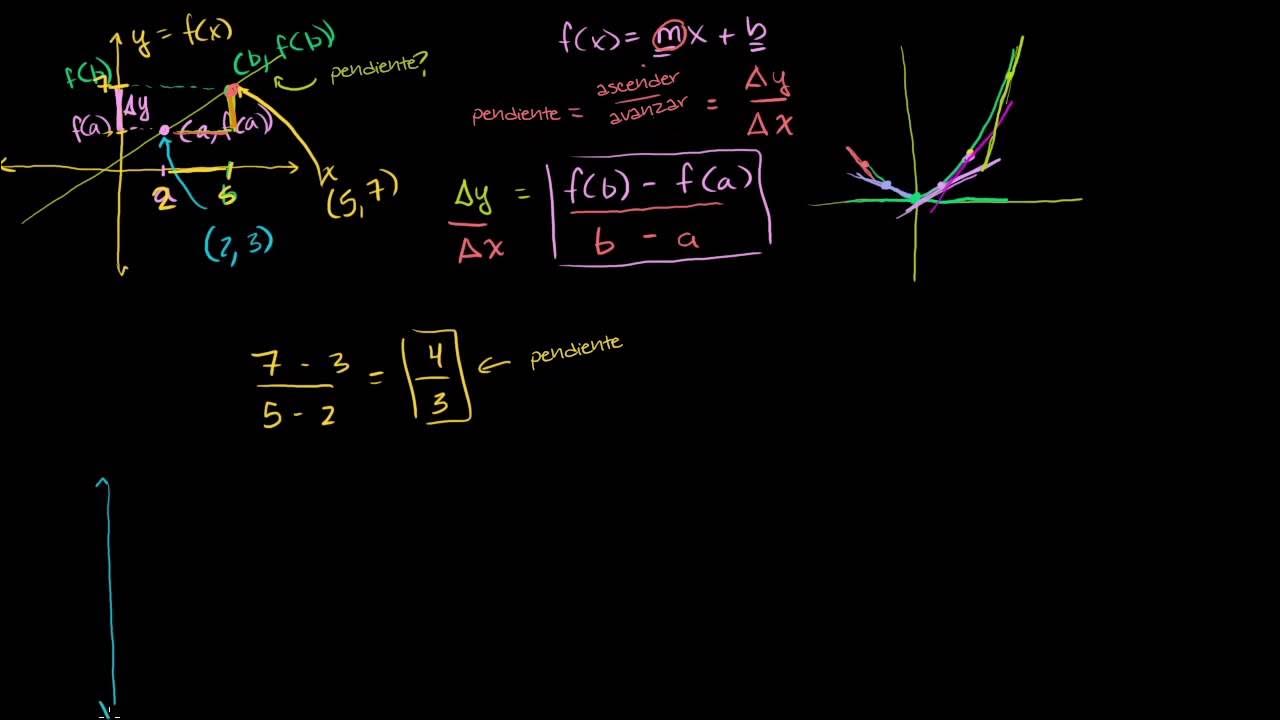
-The script defines the derivative as the limit of the ratio of the change in the output (df) to the change in the input (dx) as dx approaches 0.
What is the difference between dx and delta x in the context of limits?
-In the context of limits, dx is often used informally to represent a small change in the input, while delta x is a more formal term used in limit expressions to represent that same small change. The use of delta x emphasizes that these changes are ordinary numbers and not infinitesimals.
Why is the epsilon-delta definition of limits important?
-The epsilon-delta definition of limits is important because it provides a rigorous and unambiguous way to define what it means for one value to approach another, which is essential for a formal understanding of calculus.
What is L'Hopital's rule and how does it relate to limits?
-L'Hopital's rule is a method for evaluating limits of indeterminate forms, such as 0/0 or ∞/∞, by taking the derivatives of the numerator and denominator and evaluating the limit of the resulting expression. It relates to limits by providing a way to find the limit of a ratio when direct substitution leads to an indeterminate form.
How does the script explain the concept of approaching a limit?
-The script explains approaching a limit by discussing how the output values of a function get closer to a certain value as the input values get closer to a specific point, excluding that point itself.
Why does the script emphasize that the derivative does not involve infinitely small changes?
-The script emphasizes that the derivative does not involve infinitely small changes to avoid paradoxical ideas and to align with the rigorous formal definition of a derivative, which is based on limits and does not require the concept of infinitesimals.
What is the purpose of using different variable names like h or delta x instead of dx in formal limit definitions?
-Using different variable names like h or delta x in formal limit definitions serves to clarify that these are ordinary numbers with non-zero, finitely small sizes, and to distinguish them from the informal use of dx which is often associated with infinitesimals.
How does the script use the concept of limits to explain the behavior of functions at undefined points?
-The script uses the concept of limits to explain that even at points where a function is undefined (like 0/0), we can still discuss the behavior of the function by looking at how the function's output values approach a certain value as the input values get closer to the undefined point.
What is the significance of the function 2 + h^3 - 2^3 / h in the script?
-The function 2 + h^3 - 2^3 / h is significant because it demonstrates the concept of limits by showing how the output of the function approaches 12 as h approaches 0, even though the function is undefined at h = 0 due to division by zero.
How does the script connect the idea of limits with the concept of derivatives?
-The script connects the idea of limits with the concept of derivatives by showing that the definition of a derivative involves finding the limit of a ratio as the change in the input approaches zero, thus linking the intuitive understanding of derivatives with their formal definition.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)