Introduction to limits 2 | Limits | Precalculus | Khan Academy
Summary
TLDRIn this video, the concept of limits in calculus is introduced. The speaker explains how limits determine the value that a function approaches as the input approaches a specific point. Using the example of the function f(x) = x², the speaker demonstrates how limits work, even when the function is not directly defined at that point. The key takeaway is that limits can provide insight into the behavior of functions near points where they may not be explicitly defined, setting the stage for deeper mathematical concepts like derivatives and integrals.
Takeaways
- 📝 The presentation is an introduction to the concept of limits in calculus.
- 🟢 The limit is written as 'lim' followed by the expression and x approaching a specific value.
- 🔍 The example used is the limit of x^2 as x approaches 2, which equals 4.
- 📊 A graph of x^2 helps illustrate how the function behaves as x approaches 2.
- 🕳 A 'gap' in the function occurs when a specific value, like x=2, is defined differently, showing the purpose of limits.
- 📉 In the modified function, f(x) equals x^2 when x ≠ 2 and equals 3 when x = 2.
- 🔢 The limit still approaches 4 as x approaches 2, even though f(2) is defined as 3.
- ❓ Limits help explain function behavior when functions have discontinuities or aren't defined at certain points.
- 🤔 The key difference between limits and evaluating functions at a specific point is emphasized.
- 🎓 A more formal mathematical definition of limits (delta-epsilon) will be covered later, along with additional problem-solving.
Q & A
What is the main concept being introduced in this presentation?
-The main concept being introduced is the limit of a function, which examines what value an expression approaches as the input variable gets closer to a certain point.
How is the limit of x² as x approaches 2 calculated?
-The limit of x² as x approaches 2 is calculated by observing the behavior of the function as x gets closer to 2 from both sides. As x approaches 2, the value of x² approaches 4.
Why might someone find the concept of a limit unnecessary at first?
-At first, the concept of a limit may seem unnecessary because you can often plug in the value directly into the function, as in the case of x², where f(2) = 4. This gives the same result as finding the limit.
What variation does the speaker introduce to explain the importance of limits?
-The speaker introduces a variation where the function f(x) is defined as x² for all values except x = 2, and at x = 2, f(x) is defined to be 3 instead of 4.
What is the limit of f(x) in the modified example as x approaches 2?
-The limit of f(x) as x approaches 2 is still 4, because from both sides of 2, the function behaves like x² and approaches 4, even though f(2) is defined to be 3.
How does the graph change in the modified example where f(x) equals 3 when x equals 2?
-In the modified example, the graph of f(x) looks like the curve of x² but with a gap at x = 2. Instead of continuing smoothly, there is a hole at (2, 4), and the point (2, 3) is marked below the hole.
Why is the limit concept important in the modified example?
-The limit concept is important because it shows that even though the function value at x = 2 is different (f(2) = 3), the values around x = 2 still approach 4. This highlights that limits describe the behavior of a function near a point, even if the function is not defined or jumps at that point.
What does the limit concept reveal about the relationship between f(2) and the limit as x approaches 2?
-The limit concept reveals that f(2) does not always have to equal the limit as x approaches 2. In the modified example, the limit is 4, but f(2) is defined as 3, showing that they can be different.
What does the speaker say will be introduced in future presentations?
-In future presentations, the speaker plans to introduce the formal mathematical definition of a limit using the delta-epsilon method and to work through various problems to build intuition about limits.
Why are limits important in calculus, according to the speaker?
-Limits are important in calculus because they provide the foundation for understanding derivatives and integrals. The concept of a limit allows for precise definitions of instantaneous rates of change and areas under curves, which are essential in calculus.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
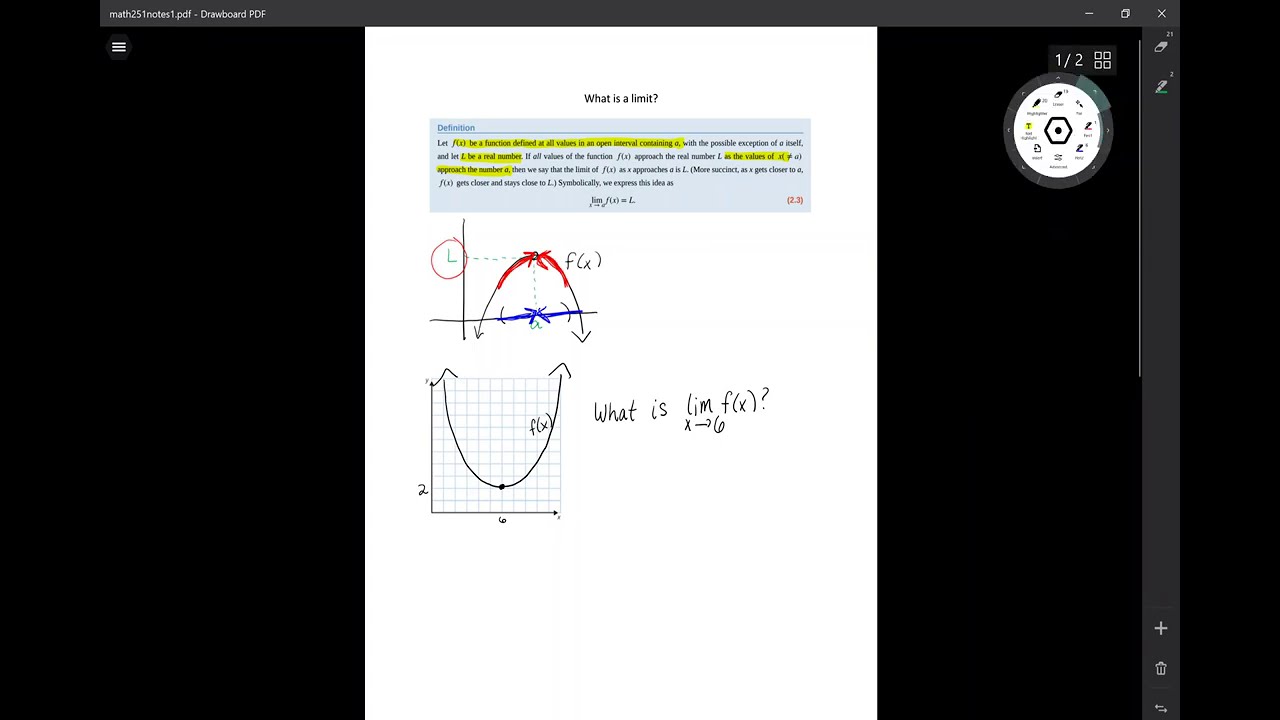
Math 251 - What is a limit?
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Calculus (Version #2) - 1.1 Limits Graphically

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)

Limit of a Function using a Graph - Basic/Differential Calculus

📚 Derivada - Definição e Cálculo - Cálculo 1 (#16)
5.0 / 5 (0 votes)
