Solución de problemas con Sistemas de Ecuaciones Lineales 2x2 | Ejemplo 3
Summary
TLDREste vídeo enseña cómo resolver problemas utilizando sistemas de ecuaciones de 2x2. Se explica el proceso paso a paso, desde nombrar las incógnitas hasta resolver el sistema usando el método de eliminación. Se ejemplifica con dos problemas: uno sobre gallinas y conejos en un corral, y otro sobre coches y motos en un parqueadero. Al final, se invita a la audiencia a practicar más y a suscribirse al canal.
Takeaways
- 📝 El vídeo enseña cómo resolver problemas utilizando sistemas de ecuaciones de 2x2.
- 🐔 Se utiliza un ejemplo clásico de gallinas y conejos en un corral para explicar el proceso.
- 🔢 Se mencionan dos ecuaciones clave: una para las cabezas (14 en total) y otra para las patas (38 en total).
- 📐 Se explica el proceso de nombrar las variables (g para gallinas y c para conejos) y escribir las ecuaciones correspondientes.
- 🧮 Se resuelve el sistema de ecuaciones utilizando el método de eliminación por reducción.
- ➗ Se multiplica la primera ecuación por -2 para eliminar la variable 'g' y resolver la variable 'c'.
- 🦙 Se descubre que hay 5 conejos en el corral.
- 🐓 Al reemplazar el número de conejos en la ecuación de cabezas, se determina que hay 9 gallinas.
- 🔄 Se recomienda verificar la solución utilizando lógica para asegurar que las patas coinciden con el número de animales.
- 🚗 Se presenta un segundo ejercicio similar pero con coches y motos en un parqueadero, utilizando el mismo enfoque.
- 🔢 Se resuelve el segundo sistema de ecuaciones y se confirma que hay 42 coches y 23 motos.
Q & A
¿Cuál es el primer paso para resolver un problema utilizando sistemas de ecuaciones de 2x2?
-El primer paso es darle nombre a lo que nos están preguntando, es decir, asignar una variable a la cantidad que queremos encontrar.
En el ejemplo de las gallinas y los conejos, ¿cuál es la variable que representa a las gallinas?
-La variable que representa a las gallinas es 'g'.
Si en un corral hay 14 cabezas y 38 patas, ¿qué ecuación representa el número total de cabezas?
-La ecuación que representa el número total de cabezas es g + c = 14, donde 'g' son las gallinas y 'c' son los conejos.
En el mismo problema, ¿cómo se representa matemáticamente el número total de patas?
-El número total de patas se representa como 2g + 4c = 38, considerando que las gallinas tienen dos patas y los conejos cuatro.
¿Qué método se utiliza para resolver el sistema de ecuaciones en el ejemplo dado?
-Se utiliza el método de reducción o eliminación para resolver el sistema de ecuaciones.
¿Cómo se elimina la variable 'g' en el método de reducción para resolver el problema de las gallinas y los conejos?
-Se multiplica toda la primera ecuación por -2 y se resta de la segunda ecuación para eliminar la variable 'g'.
Si al resolver el sistema de ecuaciones se obtiene que el número de conejos es 5, ¿cuántas gallinas hay en el corral?
-Si hay 5 conejos y en total hay 14 animales, entonces hay 9 gallinas, ya que 14 - 5 = 9.
¿Cómo se verifica que la cantidad de patas es correcta en el problema de las gallinas y los conejos?
-Se verifica multiplicando el número de gallinas por 2 y el número de conejos por 4, y sumando ambos productos para ver si dan un total de 38 patas.
En el segundo ejemplo del vídeo, ¿cuál es el nombre de la variable que representa a los coches?
-La variable que representa a los coches es 'c'.
Si en un parqueadero hay 65 vehículos y 214 ruedas, ¿cuál es la ecuación que representa el número total de ruedas?
-La ecuación que representa el número total de ruedas es 4c + 2m = 214, donde 'c' son los coches y 'm' son las motos.
¿Cómo se determina el número de motos en el parqueadero?
-Después de encontrar que hay 42 coches, se reemplaza ese número en la ecuación de los vehículos para determinar que hay 23 motos, ya que 65 - 42 = 23.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción

Solución de problemas con Sistemas de Ecuaciones Lineales 2x2 | Ejemplo 1
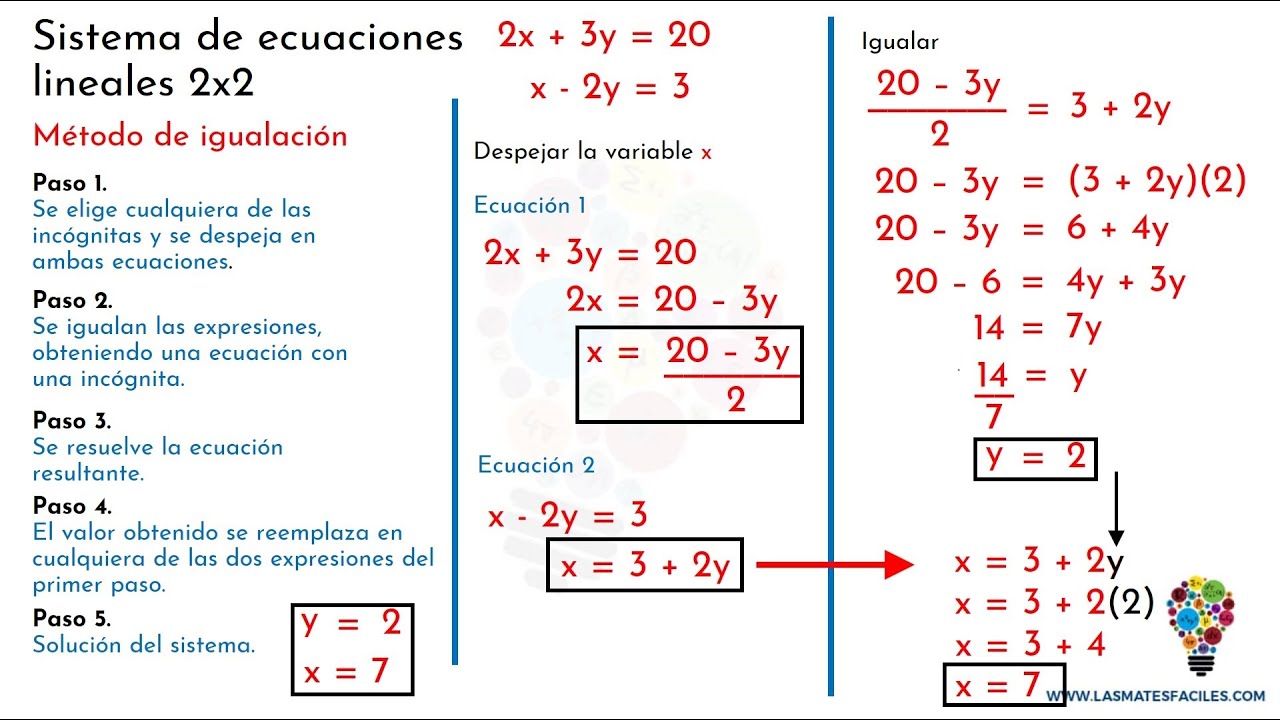
Sistemas de Ecuaciones 2x2 - Método de Igualación

Solución de problemas con Sistemas de Ecuaciones Lineales 2x2 | Ejemplo 8

RESOLVER SISTEMAS DE ECUACIONES MÉTODO DE REDUCCIÓN O SUMA Y RESTA Super fácil - Para principiantes

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1
5.0 / 5 (0 votes)
