How to Solve Quadratic Equations by Extracting the Square Root? @MathTeacherGon
Summary
TLDRIn this video, the teacher explains how to solve quadratic equations using the method of extracting square roots. This is one of several methods for solving quadratic equations, alongside factoring, completing the square, and using the quadratic formula. The video demonstrates the process with multiple examples, highlighting how to handle different forms of equations by isolating terms and extracting square roots to find both positive and negative solutions. The teacher emphasizes the importance of understanding perfect squares and offers a step-by-step approach to manipulate equations, making the process easier to grasp.
Takeaways
- 📚 The video focuses on solving quadratic equations by extracting square roots.
- 🔍 Extracting the square root is one of several methods to solve quadratic equations, alongside factoring, completing the square, and the quadratic formula.
- 🧮 If x² = k, then x = ±√k for all non-negative real numbers k.
- ✔️ When extracting the square root of a number, remember that there are always two solutions: one positive and one negative.
- 🔢 Example 1: x² = 49 gives solutions of x = ±7.
- ➕ To solve equations not in the standard form, manipulate the equation (e.g., adding or subtracting terms to isolate x²).
- 🔑 Example 2: x² - 8 = 1 is manipulated to x² = 9, yielding x = ±3.
- 🔧 For non-perfect squares (like √27), factor the number into a perfect square and simplify.
- 🌀 More complex quadratic equations, like (x - 2)² = 16, can be solved by extracting the square root and further isolating x.
- 📝 The instructor assigns item 7 as homework for viewers to practice solving quadratic equations.
Q & A
What is the focus of the video?
-The video focuses on solving quadratic equations by extracting square roots, one of the methods used to solve quadratic equations.
What other methods for solving quadratic equations are mentioned in the video?
-The methods mentioned are factoring, completing the square, and using the quadratic formula.
What property is essential when extracting square roots to solve quadratic equations?
-If x^2 = k, then x = ±√k, meaning that the square root of a number gives two values: one positive and one negative.
What is the result of solving x^2 = 49 by extracting square roots?
-The solution is x = ±7, meaning x = 7 and x = -7.
How do you manipulate an equation like x^2 - 8 = 1 to solve by square roots?
-First, add 8 to both sides to isolate x^2, resulting in x^2 = 9, then take the square root to get x = ±3.
What do you do if the number under the square root is not a perfect square, like x^2 = 27?
-You can factor the number into perfect squares and simplify. In this case, x = ±3√3.
How do you solve an equation like (x - 2)^2 = 16 using square roots?
-Take the square root of both sides to get x - 2 = ±4, then add 2 to both sides to find x = 6 and x = -2.
What is the first step in solving an equation like 2x^2 - 18 = 0?
-Add 18 to both sides to get 2x^2 = 18, then divide both sides by 2 to simplify the equation.
How do you handle an equation like (x + 10)^2 = 25?
-Take the square root of both sides to get x + 10 = ±5, then subtract 10 from both sides to find the solutions x = -5 and x = -15.
What are the possible values of x if k is positive, zero, or negative in a quadratic equation?
-If k is positive, there are two real values for x. If k is zero, there is one real value. If k is negative, there are no real values for x.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
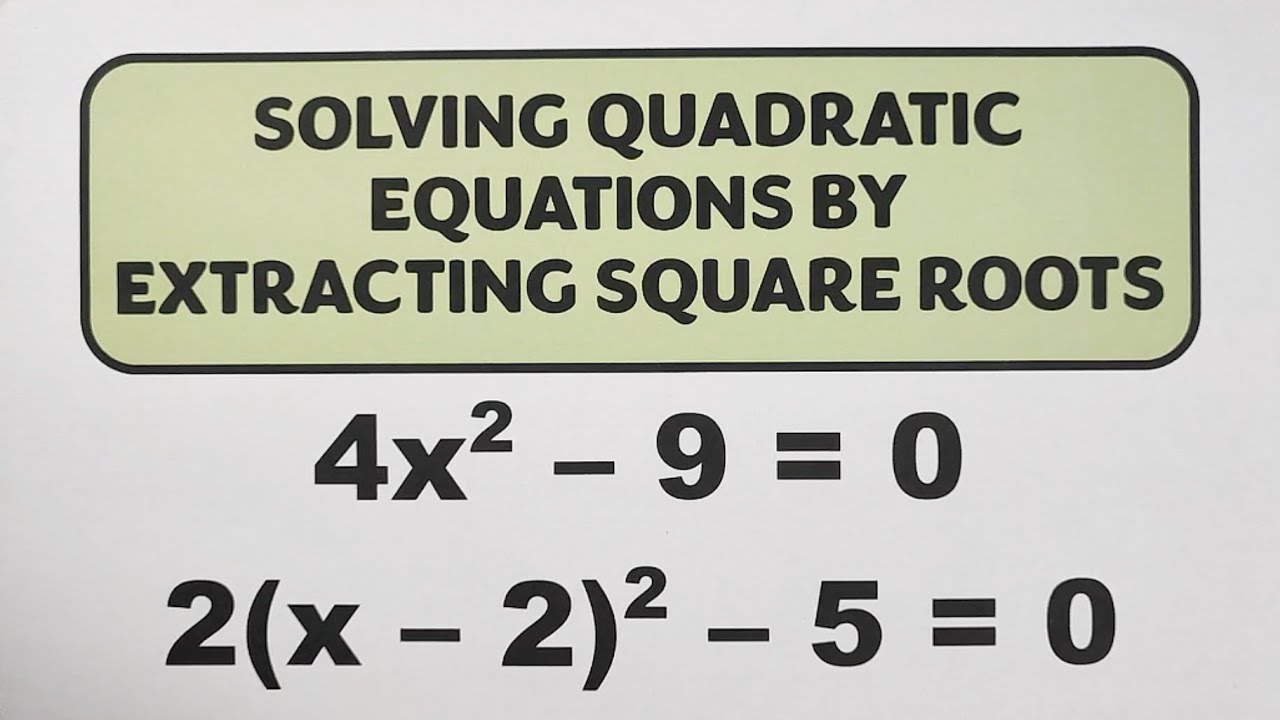
Solving Quadratic Equations by Extracting the Square Roots by @MathTeacherGon

2. Ecuaciones cuadráticas completas, solución por el Método de completar el binomio

SOLVING QUADRATIC EQUATIONS USING QUADRATIC FORMULA | Grade 9 Learning Task 3 Week 1

Persamaan Kuadrat •Part 1: Menyelesaikan Persamaan Kuadrat dengan Pemfaktoran / Faktorisasi Tipe 1&2

How to Solve These Quadratic Equations?

SOLVING QUADRATIC EQUATIONS BY EXTRACTING SQUARE ROOTS || GRADE 9 MATHEMATICS Q1
5.0 / 5 (0 votes)
